2차원과 3차원 회전의 차이

2차원의 회전과 3차원의 회전은 무엇이 다른가

차원의 차이

너무나 당연한 사실이겠지만, 2차원 회전은 평면상에서 원점을 중심으로 회전한다.
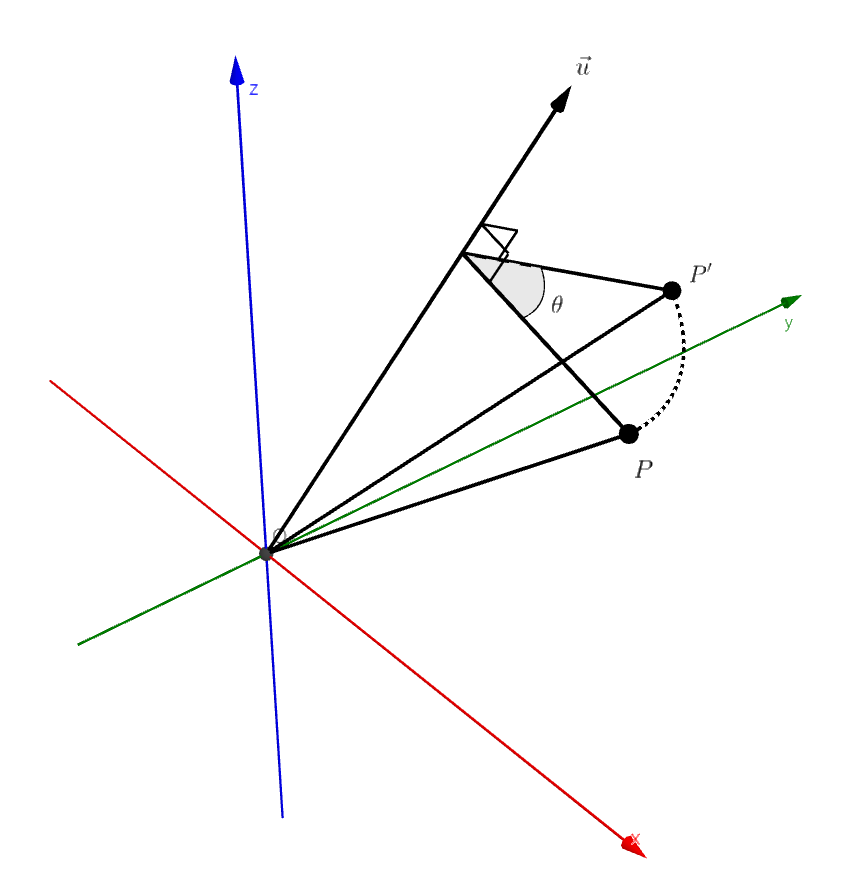
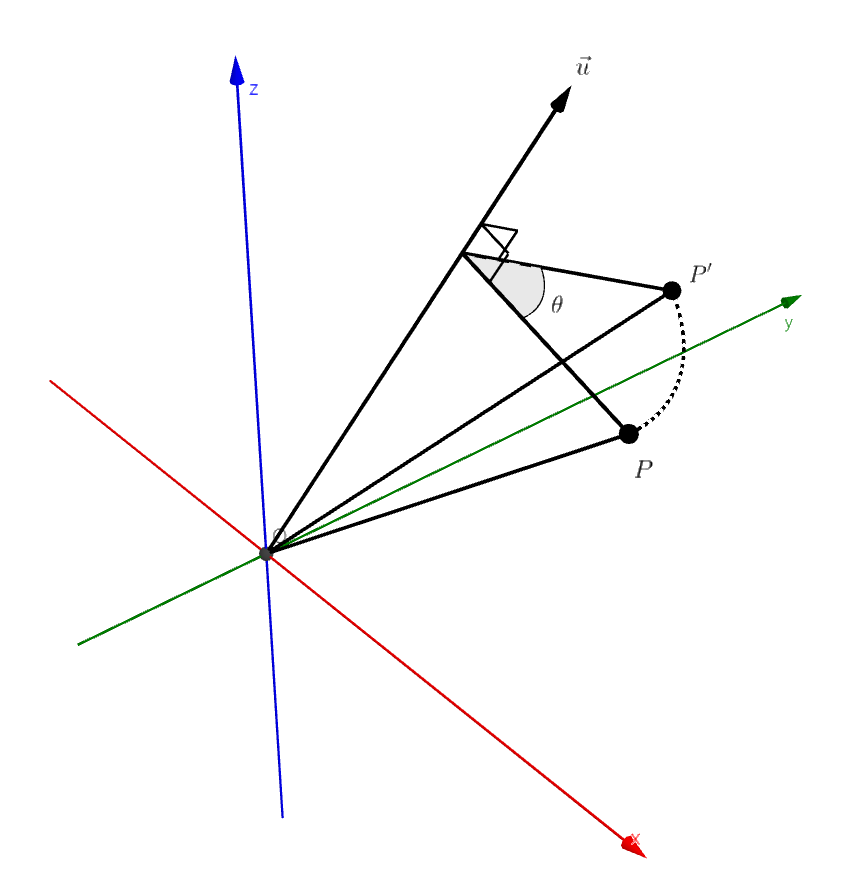
하지만 3차원 회전은 공간상에서 원점을 지나는 임의의 축을 중심으로 회전한다.

그림 1 : 임의의 축 u를 중심으로 회전하는 점 P

회전 행렬의 차이

2차원 회전 행렬은 2개의 축 벡터를 변환했기에 ($i_x, i_y -> b_x, b_y$) 회전 행렬은 $2 \times 2$의 형태였다.
3차원 회전 행렬은 3개의 축 벡터를 변환하므로 ($i_x, i_y, i_z -> b_x, b_y, b_z$) 회전 행렬은 $3 \times 3$의 형태이다.

2차원 때와 같이, 회전된 축 벡터를 그대로 사용하여 회전 행렬을 구성할 수 있다.

\[\begin{align} R_{2} &= \left[\begin{array}{c|c} b_x & b_y \end{array}\right] \nonumber \\ R_{3} &= \left[\begin{array}{c|c|c} b_x & b_y & b_z \end{array}\right] \end{align}\]

3차원 회전 행렬의 수학적인 정의는 다음과 같다

\[\begin{align} SO(3) = \left\{ R \in \mathbb{R}^{3\times3} : R^T R = I, det(R) = 1 \right\} \end{align}\]

참고 : 3D Rotation Group

여기서 $R^T R = I$인 행렬을 직교행렬(orthogonal matrix)라 하며, 열벡터와 행벡터가 전부 정규직교(orthonomal)라는 특성을 가진다.

$det(R) = 1$인 것은 앞선 포스트에서 설명했듯이, 거울 대칭 행렬과 구분하기 위함이다.

예시로 3차원 상에서 $x$축으로 $\theta$만큼 회전시키는 회전을 생각해보자.

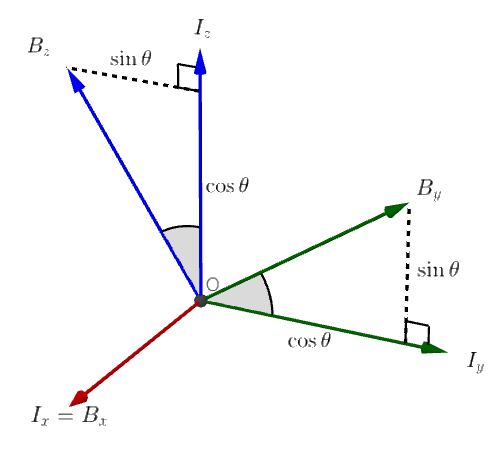그림 2 : x축으로 $\theta$만큼 회전된 좌표계

그림 2를 봤을 때, 회전 행렬 $R$은 다음과 같다.

\[\begin{align} b_x &= \begin{bmatrix}1 \\ 0 \\ 0 \end{bmatrix} \nonumber \\[15pt] b_y &= \begin{bmatrix}0 \\ \cos{\theta} \\ \sin{\theta} \end{bmatrix} \nonumber \\[15pt] b_z &= \begin{bmatrix}0 \\ -\sin{\theta} \\ \cos{\theta} \end{bmatrix} \nonumber \\[15pt] \therefore R &= \left[\begin{array}{c|c|c} b_x & b_y & b_z \end{array}\right] \nonumber \\[5pt] &= \begin{bmatrix}1 & 0 & 0 \\ 0 & \cos{\theta} & -\sin{\theta} \\ 0 & \sin{\theta} & \cos{\theta} \end{bmatrix} \end{align}\]

축 벡터의 조건 차이

3차원 좌표계의 축벡터를 구성할 때는 다음 조건들이 필요하다.

1. $\large\left\Vert i_x \right\Vert = \left\Vert i_y \right\Vert = \left\Vert i_z \right\Vert = 1$
   모든 축 벡터의 길이가 1이여야 한다.

2. $\large\vec{i_x}\bot\vec{i_y}, \vec{i_y}\bot\vec{i_z}, \vec{i_z}\bot\vec{i_x}$
   모든 축 벡터는 서로 직교해야 한다. (내적이 0인 것과 같다)

3. $\large\vec{i_x}\times \vec{i_y} = \vec{i_z}$
   $x$와 $y$방향의 외적을 $z$방향으로 정해야 한다. (오른손 법칙)

조건3은 3차원 좌표계에서 처음 등장하는 구성 조건이다.

사실, 왼손 법칙을 쓰나 오른손 법칙을 쓰나는 단순한 표기의 문제일 뿐이며 좌표계를 표현한다는 본질은 변하지 않는다.
하지만 왼손 법칙과 오른손 법칙이 사용된 좌표계가 혼용되면 혼란이 빚어질 수 있기 때문에 오른손 법칙으로 통일하는것이 원칙이다.

좌표계의 방향에 따라서 다양한 변환과 연산들의 결과가 다르게 해석되어야 하기 때문에, 오른손 법칙으로 통일하는 것은 매우 중요하다.

예를 들어, 만약 왼손 법칙을 사용한 좌표계라면 당장 벡터의 외적 방향부터 다르게 해석되어야 할 것이다.

파라미터의 개수 차이

2차원 평면상에서의 회전은 회전축이 $e_z=(0,0,1)$로 고정되어 있으므로, 회전각 파라미터 $\theta$ 하나로 회전을 결정할 수 있었다.

그러면 단순히 생각해서 3차원 공간상에서의 회전은 파라미터 2개로 결정할 수 있을까?
그렇지 않다.

3차원 공간상에서의 회전은 회전축이 공간상에 $\vec{u}, (\left\Vert u \right\Vert = 1)$로 3개의 자유도를 가진다. 거기에 돌아간 각도까지 표현해야 한다.

따라서 $\theta \cdot \vec{u} = \vec{\theta}=(\theta_x, \theta_y, \theta_z)$로 최소 3개의 각도 파라미터가 있어야 하나의 회전을 결정할 수 있다.

표현 방법의 차이

2차원 회전의 표현 방법은 3가지 정도가 있다.

1. Rotation Matrix
2. 그냥 각도 $\theta$
3. 복소수

3차원 회전의 표현 방법은 좀 더 다양하다.

1. Rotation Matrix
2. Axis-Angle (회전축과 회전 각도)
3. Euler Angle (오일러각 회전 표현)
4. Quaternion (사원수, 복소수의 확장판)

각각의 표현법 모두 장단점이 있다. 수학적으로 매끄럽거나, 사람이 직관적으로 이해하기 좋은 경우에 따라 나뉜다.

다음 포스트에서는 3차원 회전 행렬과 각속도 벡터와의 관계에 대해 설명한다