회전변환행렬의 프레임 회전변환과 자세 차이 회전

회전변환의 변환은 또 뭔

회전 변환 행렬 자체의 프레임 회전 변환에 대해 알아보자

벡터의 회전과 프레임의 회전 변환에 대해서는 이 포스트를 참고하자.

프레임 회전 변환

이전 포스트에서, 회전변환행렬 $R$을 사용해서 점 P가 어떻게 회전되는지 보였다.

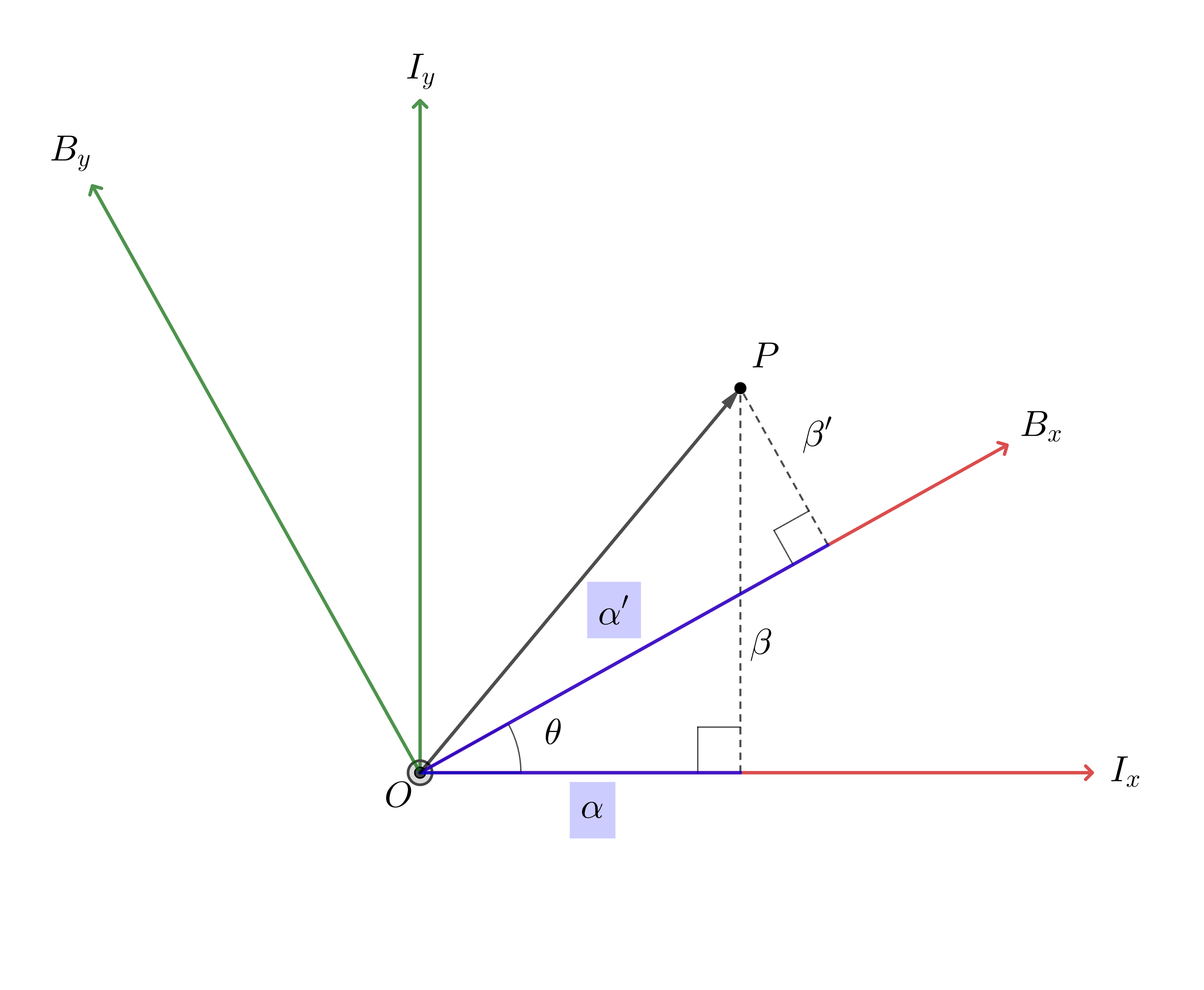그림 1: 고정된 점 P를 표현하는 2개의 프레임 좌표

그림1을 보자. 공간상에 고정된 점 $P$를 표현하는 2개의 좌표계, $I,B$가 있다. 각각의 좌표계로 점 P의 위치를 표현하는 벡터를 각각 $P_I, P_B$라 하자.
정확한 값은 그림1에서 다음과 같다.

\[\begin{align} P_I = \begin{bmatrix} \alpha \\ \beta \end{bmatrix}, P_B = \begin{bmatrix} \alpha' \\ \beta' \end{bmatrix} \end{align}\]

각 프레임의 단위 축 벡터를 $\vec{i_x}, \vec{i_y}, \vec{b_x}, \vec{b_y}$라 하자. 그리고 그냥 (0,1), (1,0) 벡터를 단위 벡터, $\vec{e_x}, \vec{e_y}$라 하자.

이때, 프레임 회전 변환 행렬, $R$에 대해서 다음이 성립한다

\[\begin{align} R\vec{i_x} &= \vec{b_x}, R\vec{i_y}=\vec{b_x}, \\ \text{as, }R^{-1} = R^T, R^T\vec{b_x} &= \vec{i_x}, R^T\vec{b_y} = \vec{i_y} \end{align}\]

이때, $P_I \rightarrow P_A$로 가는 변환은 다음과 같다.

\[\begin{align} R^T P_I &= R^T\left( \alpha \vec{i_x} + \beta\vec{i_x} \right) \nonumber \\[5pt] &= R^T\left( \alpha' \vec{b_x} + \beta' \vec{b_x} \right) \nonumber \\[5pt] &= \alpha' R^T \vec{b_x} + \beta' R^T \vec{b_y} \nonumber \\[5pt] &= \alpha' \vec{i_x} + \beta' \vec{i_y} = \begin{bmatrix} \alpha' \\ \beta' \end{bmatrix} \nonumber \\[5pt] \therefore R^T P_I &= P_B \\ \therefore R P_B &= P_I \label{e1} \end{align}\]

이는 3차원 공간으로 가도 동일하게 적용할 수 있으므로, 3차원의 회전 변환에 대해서도 적용 가능하다.

벡터 회전 행렬의 프레임 회전 변환

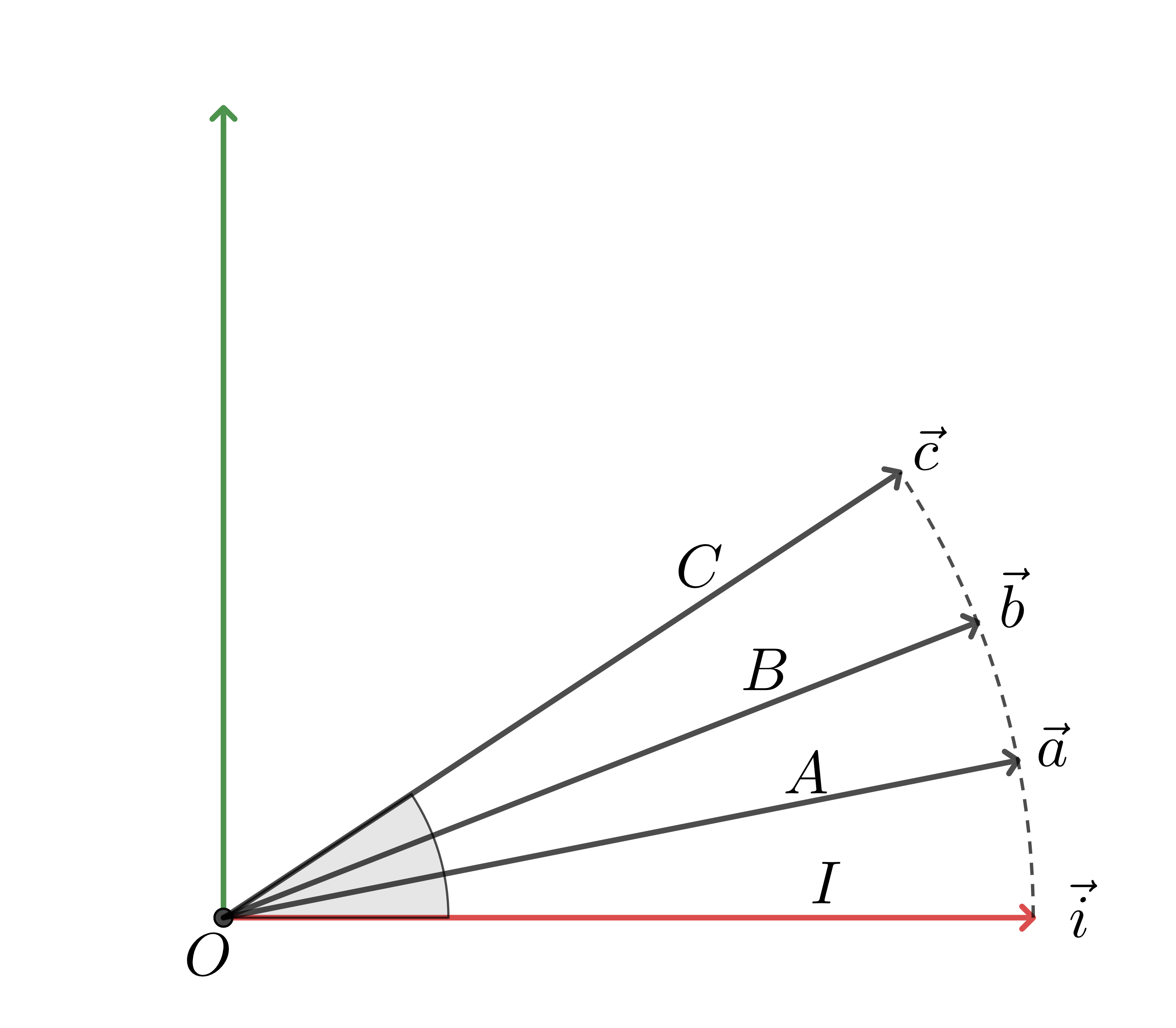그림 2: 프레임 I,A,B,C와, 회전된 벡터 i,a,b,c들

그림2를 보자.
총 4개의 프레임이 있는데, 기준 좌표계가 되는 $I$와, 각각 일정 각도로 회전된 프레임 $A,B,C$가 있다. 기준 좌표계의 벡터 $\vec{i}$가 프레임만큼 회전된 벡터들을 각각 $\vec{a}, \vec{b}, \vec{c}$라 하자. 기준 좌표계를 각각의 프레임으로 회전시키는 행렬을 $R_A, R_B, R_C$라 하자.
벡터에 대해서 $\vec{v}^K$는 $K$프레임으로 표현된 벡터 $\vec{v}$를 의미한다.

다음이 성립한다.

\[\begin{align} R_A\vec{i}^I = \vec{a}^I, \nonumber \\ R_B\vec{i}^I = \vec{b}^I, \nonumber \\ R_C\vec{i}^I = \vec{c}^I \nonumber \\ \nonumber \\ \vec{v} \in {\vec{i}, \vec{a}, \vec{b}, \vec{c}} \nonumber \\ (R_A)^T \vec{v}^I = \vec{v}^A \nonumber \\ (R_B)^T \vec{v}^I = \vec{v}^B \nonumber \\ (R_C)^T \vec{v}^I = \vec{v}^C \nonumber \\ \end{align}\]

이제 다음 벡터 변환은 어떻게 될지 생각해 보자

\[\begin{align} \vec{a}^I \rightarrow \vec{b}^I ? \nonumber \\ \nonumber \\ (R_A)^T \vec{a}^I &= \vec{i}^I, \nonumber \\ R_B \vec{i}^I &= \vec{b}^I.\nonumber \\ \nonumber \\ \therefore R_B (R_A)^T \vec{a}^I &= \vec{b}^I \nonumber \\ \nonumber \\ \therefore R_{A \rightarrow B}^I &= R_B (R_A)^T \label{e2} \\ R_{A \rightarrow B}^I \vec{a}^I &= \vec{b}^I \nonumber \end{align}\]

식 $\eqref{e2}$가 의미하는 바는, $I$에서 봤을 때, $\vec{a} \rightarrow \vec{b}$로 변환하는 행렬이다.
어떻게 보면 두 자세 사이의 차이에 대한 회전 행렬이라고 볼 수 있겠다.

이제 진짜 목적으로 들어가 보자 \(\begin{align} \vec{a}^C \rightarrow \vec{b}^C ? \nonumber \\ \nonumber \\ R_C \vec{a}^C &= \vec{a}^I, \nonumber \\ (R_A)^T \vec{a}^I &= \vec{i}^I, \nonumber \\ R_B \vec{i}^I &= \vec{b}^I, \nonumber \\ (R_C)^T \vec{b}^I &= \vec{b}^C \nonumber \\ \nonumber \\ \therefore (R_C)^T R_B (R_A)^T R_C \vec{a}^C &= \vec{a}^C \nonumber \\ \therefore R_{A \rightarrow B}^C &= (R_C)^T R_{A \rightarrow B}^I R_C \label{e3} \\ R_{A \rightarrow B}^C \vec{a}^C &= \vec{b}^C \nonumber \end{align}\)

식 $\eqref{e3}$에서 재미있는 관계식을 찾을 수 있다. 다른 프레임으로 표현된 벡터의 회전 행렬을 만들고 싶다면, 그 회전 행렬을 양쪽에 감싸면 된다.
즉, 요약하면 다음과 같다.

$\vec{v}^K$ : 프레임 $K$에서 표현한 벡터 $\vec{v}$

\[\begin{align} R_{A \rightarrow B}^C \vec{a}^C = \vec{b}^C \nonumber \\ \nonumber \\ R_{A \rightarrow B}^C = \left(R_{I \rightarrow C}\right)^T R_{A \rightarrow B}^{I} R_{I \rightarrow C} \label{e4} \end{align}\]

첫번째로,만약 $R_{A \rightarrow B}^I \rightarrow R_{I \rightarrow A}^I$로 바뀐다면?

\[\begin{align} R_{I \rightarrow A}^C &= (R_C)^T R_{I \rightarrow A}^I R_C, \\ &= (R_C)^T R_A R_C \nonumber \\ R_{I \rightarrow A}^C \vec{i}^C &= \vec{a}^C \nonumber \end{align}\]

두번째는, 만약 $C \rightarrow A$ 라면?

\[\begin{align} R_{A \rightarrow B}^A &= (R_A)^T R_{A \rightarrow B}^I R_A \nonumber \\ &= (R_A)^T R_B (R_A)^T R_A = R_A^T R_B \\ R_{A \rightarrow B}^A \vec{a}^A &= \vec{b}^A \nonumber \end{align}\]

헷갈리는 자세 차이 행렬 정리

어떠한 자세 $R_A$와 $R_B$의 차이를 계산해야 할 때, 다음의 두가지 방법이 있다.

1. $R_{A \rightarrow B}^I = R_B (R_A)^T$
   $R_{A \rightarrow B}^I \vec{a}^I = \vec{b}^I$
   이 변환 방법은 회전 행렬의 기준이 됐던 기준 프레임 $I$에서 관찰한 벡터들의 값을 변환한다.
   회전변환된 2개의 벡터, $a,b$가 프레임 $I$에서 관찰된 값을 변환한다.
   관성 기준 좌표계에서 자세의 차이를 보고 싶을 때 사용한다.

2. $R_{A \rightarrow B}^A = (R_A)^T R_B$
   $R_{A \rightarrow B}^A \vec{a}^A = \vec{b}^A$
   이 변환 방법은 프레임 $A$에서 관찰한 벡터들의 값을 변환한다.
   회전변환된 2개의 벡터 $a,b$가 프레임 $A$에서 관찰된 값을 변환한다.
   Body 좌표계에서 자세의 차이를 보고 싶을 때 사용한다.

예를 들어, 공간상의 강체에 붙은 Body 좌표계 $B$와, 목표 자세 좌표계 $C$가 있다고 하자.
이때, 기준좌표계 $I$에서 각각의 좌표계 basis로의 회전 행렬을 $R_B, R_C$라 하자.

$R_{B \rightarrow C}^I = R_C (R_B)^T$는 기준계 $I$에서 바라본, 현재 Body Frame의 자세로부터 목표 자세까지의 차이에 대한 회전 행렬이다.
$R_{B \rightarrow C}^B = (R_B)^T R_C$는 Body frame에서 바라본, 현재 자세로부터 목표 자세까지의 차이에 대한 회전 행렬 행렬이다.

이 부분은 복소수, 사원수에도 동일하게 적용되는 부분이며, 나중에 자세 쿼터니언을 가지고 제어 컨트롤러를 설계할 때 다시 보게 된다.