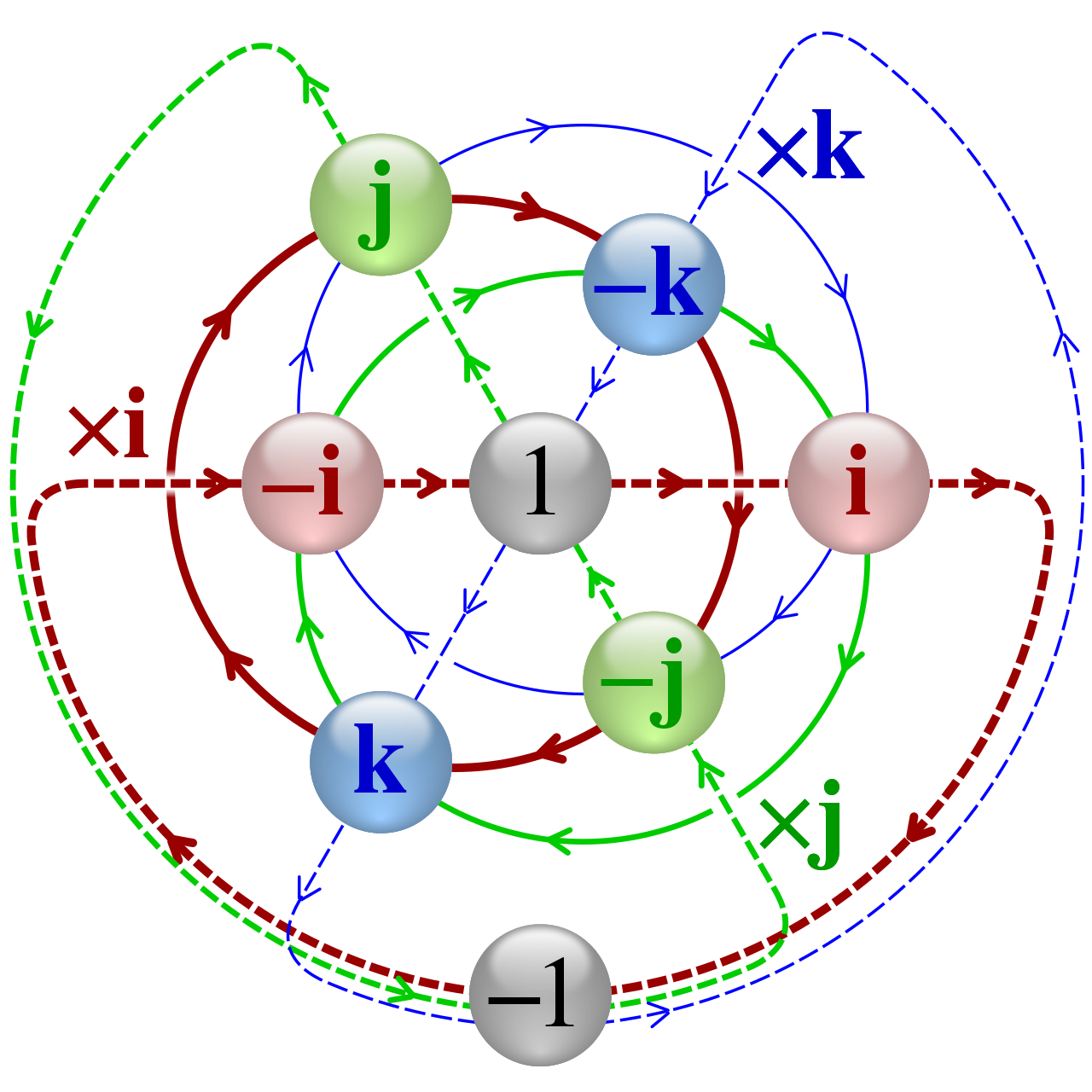
복소수의 확장, 사원수(쿼터니언, Quaternion)
사원수(쿼터니언, Quaternion)은 대체 무엇일까
참고 및 출처: Quaternion
3차원 회전의 완전체, 사원수에 대한 기본 개념들을 알아보자.
쿼터니언의 정의
사원수(Quaternion)은 3차원에서 벡터의 회전, 또는 물체의 자세를 표현하는 수학적인 방법 중 하나이다.
쉽게 생각해서 2차원의 자세를 표현하는 수가 복소수였다면, 3차원의 회전을 표현하는 수는 사원수이다.
제일 기본적인 표기 방법은 다음과 같다.
\[\begin{align} q\text{(Quaternion)} &= w + xi + yj + zk, (w,x,y,z \in \mathbb{R})\nonumber \\ i^2 &= j^2 = k^2 = ijk =-1 \nonumber \\ i,j,k &: \text{basis vector} \label{e1} \end{align}\]
주의할 점은, $ijk$와 $kji$는 서로 다른 값이다. 즉, basis 들의 곱은 교환법칙이 성립하지 않는다(non-commutative).
종종 w와 x,y,z를 따로 묶어서 실수부와 허수부(또는 벡터부, vector part)라고 하기도 하며, 이렇게 표기하기도 한다.
\[\begin{align} q = w + \vec{v}, (\vec{v}=(x,y,z)) \label{e2} \end{align}\]
쿼터니언의 발견
쿼터니언은 1845년 헤밀턴(Hamilton)에 의해 처음 발명되었다.
그 당시 헤밀턴은 더 높은 차원에서의 복소수를 찾고 있었다. 기존의 복소수가 2차원의 회전을 완벽하게 설명했듯이, 3차원의 회전을 완벽하게 설명하는 새로운 수 체계를 찾아 헤맸다.
헤밀턴은 2개의 실수로 표현되는 복소수가 2차원의 회전을 설명했으므로, 3개의 실수로 이루어진 어떤 수에 basis vector들의 연산 규칙을 적절히 추가하면 3차원 버전으로 확장 될 것이라 생각했다.
기존의 2차원 회전을 서술하는 복소수는
체(field)이다.
대수구조의 한 종류로, 우리가 생각하는 일반적인 사칙연산이 전부 통하는 가장 편안한 구조라고 생각하면 된다.
주로 다음의 규칙들이 있다.
예를 들어 임의의 세 복소수, $a,b,c \in \mathbb{C}$에 대해서 다음이 성립해야 한다.
닫힘
모든 원소들의 덧셈과 곱셈의 결과도 복소수이다. $a+b,ab \in \mathbb{C}$결합법칙의 성립
덧셈과 곱셈의 결합법칙이 성립한다.
$(a+b)+c = a+(b+c)$
$(ab)c = a(bc)$교환법칙의 성립
덧셈과 곱셈의 교환법칙이 전부 성립한다.
$a+b = b+a$
$ab = ba$덧셈과 곱셈의 항등원이 존재하며, 복소수이다
$a+0=a, a \times 1 = a$
$0,1 \in \mathbb{C}$덧셈의 역원이 존재하며, 복소수이다
$a+(-a) = 0, -a \in \mathbb{C}$0이 아닌 원소에 대해 곱셈의 역원이 존재하며, 복소수이다
$\text{where }a \neq 0, a \cdot \large \left(\frac{\bar{a}}{\lvert a \rvert^2}\right) = 1, \frac{\bar{a}}{\lvert a \rvert^2} \in \mathbb{C}$분배법칙이 성립한다
$a(b+c) = ab+ac$
복소수는 위의 특징들을 모두 만족하므로, 체(field) 이며, 이는 우리가 매우 익숙한 실수($\mathbb{R}$)과 같은 대수구조를 가진다. 즉 일반적인 실수의 연산처럼 자유롭게 사칙연산을 해도 괜찮다는 뜻이다.
하지만 여기서 더 나아간 3차원 회전을 기술하는 확장된 복소수(임의로 $n$ 이라 하겠다)는 한가지 성질을 잃어버려야 하는데, 그것은 바로 곱셈의 교환법칙이 성립하면 안된다는 것이다.
이를 표현하면 $n_1 n_2 \neq n_2 n_1$가 되어야 한다는 뜻이다. 직전에 포스팅했던 오일러 각으로 빗대어 보면, $R_x(\theta_x)R_y(\theta_y) \neq R_y(\theta_y)R_x(\theta_x)$ 였던 것과 같다.
따라서 우리가 찾고자 하는 확장된 복소수 체계는 체가 아니라 나눗셈 환(division ring) 대수구조를 갖게 된다. 체에서 곱셈의 교환법칙이 성립하지 않는 경우다.
환(ring) 중에서 곱셈의 교환법칙이 성립하는 환을 가환환이라 하며, 가환환이면서 나눗셈환인 구조가 체다
하지만, $a+bi+cj$의 구조에서는 0이 아닌 모든 원소의 역원이 존재할 수 없었다. 덧셈은 가능했지만 나눗셈이 도저히 해결되지 않았던 것이다.
그러던 어느날, 헤밀턴은 Royal Canal 다리를 지나다가 문득 아이디어 하나를 떠올린다. 3차원이 아니라 4차원의 수라면 이 모든 것이 가능하다는 것을.
그는 그 다리에 임시로 머릿속에 떠오른 이 새로운 수의 연산 법칙을 적어 넣었으니, 다음과 같았다.
사원수(Quaternion)은 나눗셈 환(division ring)이다.
나눗셈 환(division ring) : 곱셈의 교환법칙이 성립하지 않는 체(field)
발견 그 이후..
헤밀턴의 사원수의 발견이후, 당시 물리학자들과 수학자들은 이 새로운 수 체계를 사용하기 시작했다.
하지만 벡터 미적분학이 발전함에 다라, 사원수는 대부분의 분야에서 밀려났는데, 벡터 방식이 더 직관적이고 다양한 분야에 적용하기 쉬웠기 때문이다.
공과대학 신입생들에게 4차원을 상상하게 하는 것은 너무나 힘들었고, 필자 역시 지금까지도 상상이 안된다. 차라리 앞서 소개했던 로드리게스 회전이나 오일러각 표현법은 3차원의 상상력만으로 충분하므로 훨씬 이해시키기 쉽다는게 당시의 이유였다.
그러나 20세기 중후반부터 컴퓨터 그래픽스와 제어 이론, 로보틱스 분야의 발달과 함께 사원수는 빛을 보게 된다.
사원수가 기존 대비 여러 방면에서 유용했는데 그 이유는 다음과 같다.
짐벌락이 없다
오일러 각과 다르게, 쿼터니언은 짐벌락이 아예 없다. 어떠한 자세에서도 원하는 각속도를 쿼터니언의 변화량을 사용해 표현할 수 있다.
짐벌락에 시달렸던 아폴로 11호의 관계자들이 얼마나 열받았을지 상상해 본다면, 이게 얼마나 행복한 일인지 알게 된다.효율적이다
쿼터니언 회전은 컴퓨터에게 있어 정말 효율적이며, 반복적인 회전 연산에도 상대적으로 안정하다. 회전 변환을 하는 방식도 행렬 형태로 바꿀 수 있어 유용하다.보간
이상하게 움직였던 기존의 회전 방식들(axis-angle, 오일러 각)들의 선형 보간(linear interpolation, LERP)와는 달리, 쿼터니언은 구면 보간(Spherical interpolation, SLERP)가 가능하다. 이는 어떤 회전 방식보다도 부드럽게 움직이며, 회전 행렬보다도 컴퓨팅에 더 효율적이다.간결성
쿼터니언은 4개의 숫자(1개의 실수부와 3개의 벡터부)만 있으면 표시할 수 있다. 이는 숫자를 9개나 저장해야 하는 회전행렬보다 메모리 크기에서 이득이다.
쿼터니언은 3차원 자세를 표현하는 새로운 기준이며, 이미 다양한 유관 분야(제어, 게임 등)에 깊게 침투해 있다.
당장에 unity 게임엔진 튜토리얼만 봐도, Euler Angle과 Quaternion 클래스에 대한 설명이 나오며, SLERP 함수를 소개하고 있다. 또, 비행체의 3차원 자세 제어에 관련된 논문에도 십중팔구 쿼터니언이 등장한다.
쿼터니언의 연산
쿼터니언 역시 복소수의 확장판이고 결국은 ‘수’ 이다. 다양한 정의를 쿼터니안으로 확장시킬 수 있는데, 다음과 같다.
$q \in \mathbb{H}, q=w+xi+jk+zk$
실수부, 허수부
$q=w+xi+yj+zk, \vec{v}=(x,y,z)$라 할 때, $w$를 실수부, $\vec{v}$를 허수부라 한다.크기(절대값)
$\lvert q \rvert = \sqrt{w^2+x^2+y^2+z^2} = \sqrt{w^2+\lVert \vec{v} \rVert^2}$덧셈
$q_1 + q_2 = (w_1 + w_2) + (x_1 + x_2)i + (y_1 + y_2)j + (z_1+z_2)k$곱셈
$q_1 \otimes q_2 = (w_1 + x_1i+y_1j+z_1k)(w_1 + x_1i+y_1j+z_1k)$
이제 위 식을 전개하면서 $i^2=j^2=k^2=ijk=-1$으로 정리하면 다음과 같다.
복소수의 곱셈에 비해서 복잡도가 많이 증가한 모습이다. 물론 이렇게 매번 복잡하고 힘들게 계산할 필요는 없다. 곱을 다르게 계산하는 여러가지 형태가 있기 때문.
공액(Conjugate)
$\bar{q} = \overline{w+\vec{v}} = w - \vec{v}$
$q \otimes \bar{q} = \lvert q \rvert^2$순사원수(pure quaternion)
실수부가 0인 쿼터니언들을 pure quternion이라 한다.
$w=0, q = \vec{v}$
쿼터니언 곱의 행렬 표현
앞의 식 $\eqref{e3}$를 노가다로 하나하나 비교해서 행렬 형태로 표현해볼 수도 있겠지만, 더 좋은 방법이 있다.
포스트 각도 표현의 미분 불가능 문제와 복소수#복소수 곱셈의 행렬 표현에서 복소수-복소수 곱셈의 행렬 표현 부분을 보자.
복소수의 곱의 연산을 다음과 같이 행렬 형태로 바꿀 수 있었다.
\[\begin{align} z = a+bi \nonumber \\ \begin{bmatrix} 1/1 & 1/i \\ i/1 & i/i \end{bmatrix} \begin{bmatrix} 1 \\ i \end{bmatrix} &= \begin{bmatrix} \text{Real Part} \\ \text{Img Part} \end{bmatrix} \nonumber \\[10pt] \therefore \begin{bmatrix} 1/1 & 1/i \\ i/1 & i/i \end{bmatrix} &= \begin{bmatrix} 1 & -i \\ i & 1 \end{bmatrix} \nonumber \\[10pt] &= \begin{bmatrix} a & -b\\ b & a \end{bmatrix} \nonumber \end{align}\]이와 같이, 쿼터니언도 바꿔볼 수 있다.
\[\begin{align} q = w + xi+yj+zk \nonumber \\ \begin{bmatrix} 1/1 & 1/i & 1/j & 1/k \\ i/1 & i/i & i/j & i/k \\ j/1 & j/i & j/j & j/k \\ k/1 & k/i & k/j & k/k \end{bmatrix} \begin{bmatrix}1 \\ i \\ j \\ k\end{bmatrix} &= \begin{bmatrix} \text{Real part} \\ \text{Im i part} \\ \text{Im j part} \\ \text{Im k part} \end{bmatrix} \nonumber \\[10pt] \begin{bmatrix} 1/1 & 1/i & 1/j & 1/k \\ i/1 & i/i & i/j & i/k \\ j/1 & j/i & j/j & j/k \\ k/1 & k/i & k/j & k/k \end{bmatrix} &= \begin{bmatrix} 1 & -i & -j & -k \\ i & 1 & -k & j \\ j & k & 1 & -i \\ k & -j & i & 1 \end{bmatrix} \nonumber \\[10pt] \therefore [q]_\times &= \begin{bmatrix} w & -x & -y & -z \\ x & w & -z & y \\ y & z & w & -x \\ z & -y & x & w \end{bmatrix} \label{e5} \end{align}\]따라서 식 $\eqref{e5}$의 쿼터니언 곱셈 행렬을 사용해서 곱셈을 다시 표현하면 다음과 같다.
\[\begin{align} q_1, q_2 \in \mathbb{H},& (q_n = w_n +x_n i + y_n j + z_n k) \nonumber \\ q_1 \otimes q_2 &= \begin{bmatrix} w_1 & -x_1 & -y_1 & -z_1 \\ x_1 & w_1 & -z_1 & y_1 \\ y_1 & z_1 & w_1 & -x_1 \\ z_1 & -y_1 & x_1 & w_1 \end{bmatrix} \begin{bmatrix} w_2 \\ x_2 \\ y_2 \\ z_2 \end{bmatrix} \nonumber \\ &= [q_1]_\times q_2 \nonumber \end{align}\]다음 포스트는 쿼터니언을 사용하여 어떻게 3차원 벡터를 회전시키는 지에 대해 포스팅 하겠다.