로드리게스 회전(Rodrigues rotation)

임의의 축에 대한 벡터의 회전, 로드리게스 회전에 대해 알아보자.

참고 : Rodrigues’ rotation formula

로드리게스 회전 공식

지금까지 2D 평면에서는 회전축이 항상 평면에 수직인 축 (가상의 $z$축)이었기에, 회전된 각도 $\theta$만으로 결정할 수 있었다.
하지만 3D 공간에서는 회전축이 완전한 자유도를 가진 단위벡터 $\vec{u}$로 표시되므로, 이제 기존의 회전 각도 $\theta$에 회전축 벡터 $\vec{u}$까지 생각해야 한다.

이를 사용하여 공간상의 벡터를 회전시키는 방식을 로드리게스 회전(Rodrigues rotation) 이라 한다.

로드리게스 회전 공식은 벡터 $\vec{v}$를 회전축 $\vec{u}$에 대해 각도 $\theta$만큼 회전시키는 공식이며, 다음과 같다.

\[\begin{align} \vec{v_{rot}} = \vec{v} \cos{\theta} + \left(\vec{u} \times \vec{v} \right) \sin{\theta} + \vec{u} \left(\vec{u} \cdot \vec{v} \right)\left( 1 - \cos{\theta} \right) \label{e1} \end{align}\]

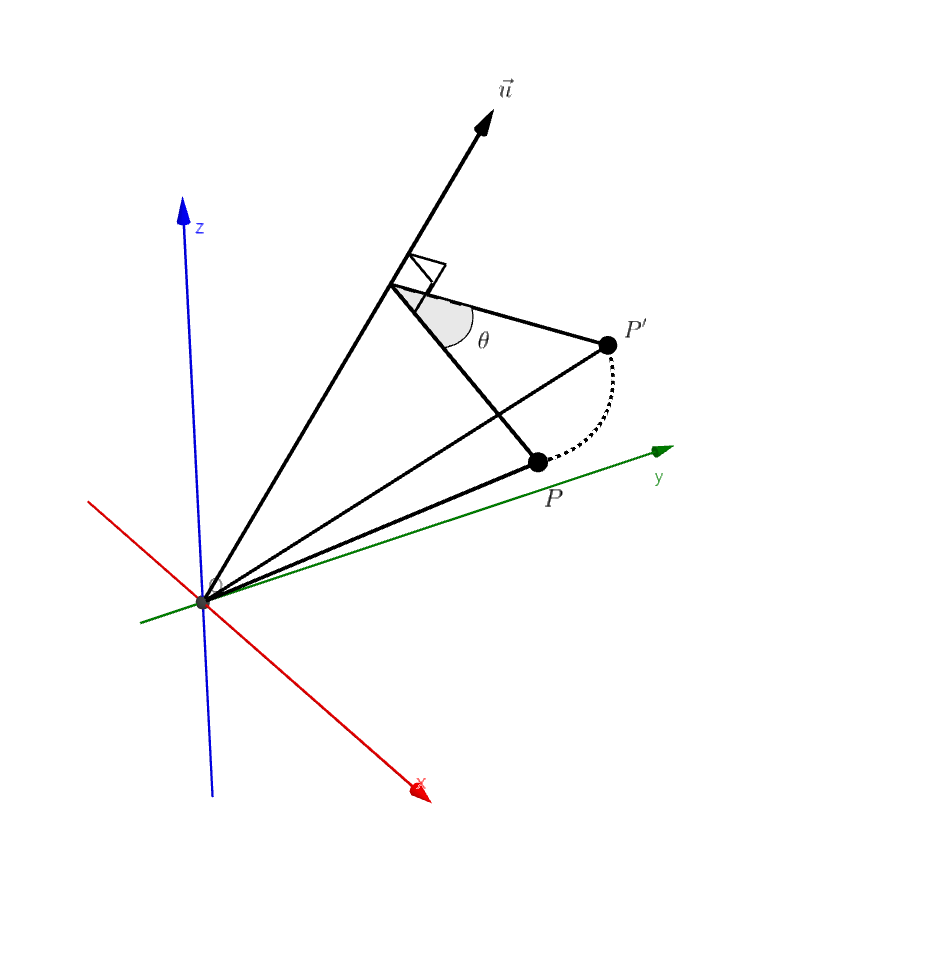그림 1: 임의의 축 $u$에 대해 회전된 벡터 $\vec{v}$

로드리게스 회전 공식의 유도

그림1을 통해 회전시킬 벡터를 회전되는 벡터와 회전되지 않는 2개의 벡터로 분리 할 수 있다.

그 중 회전축에 평행한 성분을 $\vec{v_{\parallel}}$, 회전축에 수직인 성분을 $\vec{v_{\bot}}$라 했을 때, 다음과 같이 표현할 수 있다.

\[\begin{align} \vec{v} &= \vec{v_{\parallel}} + \vec{v_\bot} \\ \vec{v'} &= \vec{v_{\parallel}} + \vec{v_\bot'} \\ \end{align}\]

이제 주어진 값들로 $\vec{v_\parallel}, \vec{v_\bot}, \vec{v_\bot’}$을 유도하겠다.

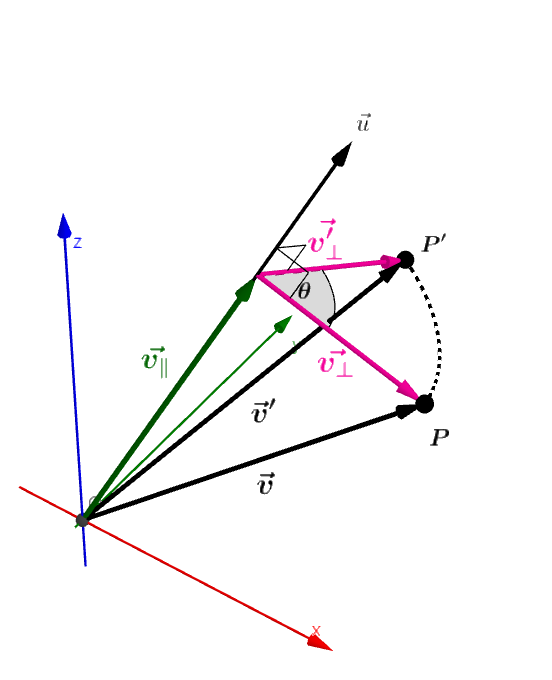그림 2: 회전된 벡터를 여러개의 벡터 성분으로 분해해 본다

그림2를 통해 $\vec{p_\parallel}$을 유도할 수 있다.

\[\begin{align} \vec{v_\parallel} &= k\vec{u}, k \in \mathbb{R} \nonumber \\ \nonumber \\ \lVert \vec{v_\parallel} \rVert &= k \lVert \vec{u} \rVert \nonumber \\ &= k \nonumber \\ &= \cos{\alpha} \cdot \lVert \vec{v} \rVert \cdot \lVert \vec{u} \rVert \nonumber \\ &= \vec{u} \cdot \vec{v} \nonumber \\ \nonumber \\ \therefore \vec{v_\parallel} &= (\vec{u}\cdot\vec{v})\vec{u} \label{ev1} \end{align}\]

다음으로 $\vec{p_\bot}$은 다음과 같다.

\[\begin{align} \vec{v} &= \vec{v_\parallel} + \vec{v_\bot} \nonumber \\ \therefore \vec{v_\bot} &= \vec{v} - \vec{v_\parallel} \nonumber \\ &= \vec{v} - (\vec{u} \cdot \vec{v}) \vec{u} \label{ev2} \end{align}\]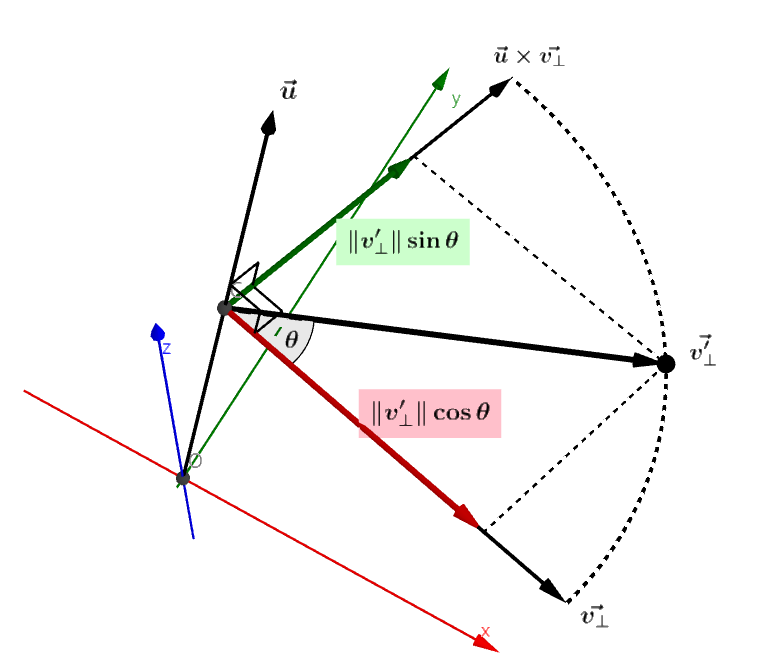

그림 3: 회전된 벡터가 놓여있는 평면의 좌표계 벡터들

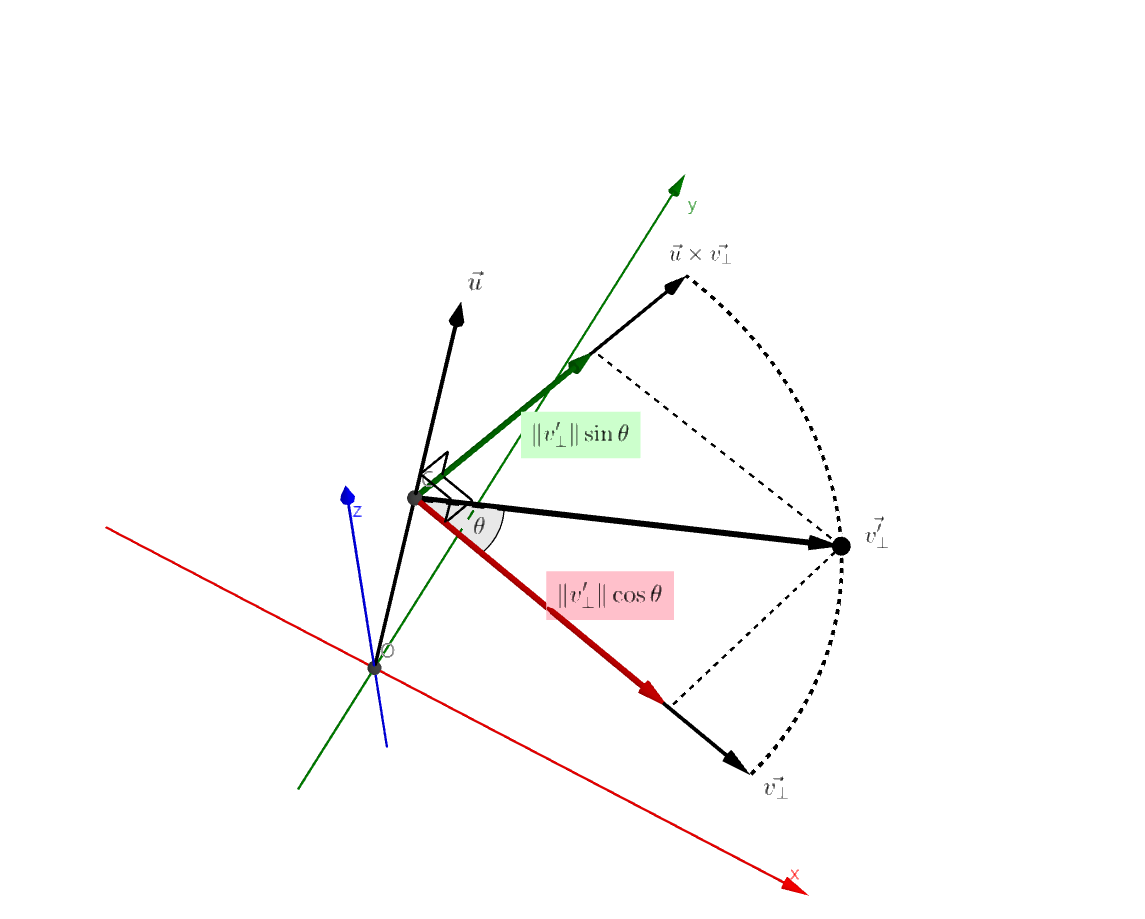
그림3을 통해 $\vec{v_\bot’}$을 유도할 수 있다.
공간상에 $\vec{u}$와 수직이고, $\vec{v_\bot}$을 포함하는 평면 상에서 $\theta$만큼 회전된 벡터이다.

해당 평면을 보면, 마치 2차원 평면에서 벡터가 $\theta$만큼 회전하듯이 움직일 것이다.
이때 $x$축 방향을 $\vec{v_\bot}$, $y$축 방향은 $\vec{u} \times \vec{v_\bot}$ 으로 잡을 수 있다.

따라서 $\vec{v_\bot’}$는 다음과 같다

\[\begin{align} \lVert \vec{v_\bot'} \rVert &= \lVert \vec{v_\bot} \rVert \\[5pt] \lVert \vec{u} \times \vec{v_\bot}\rVert &= \lVert \vec{u} \rVert \lVert \vec{v_\bot} \rVert \sin{0.5\pi} = \lVert \vec{v_\bot} \rVert \\ \nonumber \\ \therefore \vec{v_\bot'} &= \lVert v_\bot \rVert \cos{\theta} \frac{\vec{v_\bot}}{\lVert v_\bot \rVert} + \lVert v_\bot \rVert \sin{\theta} \frac{\vec{u}\times\vec{v_\bot}}{\lVert \vec{u} \times \vec{v_\bot} \rVert} \nonumber \\[10pt] &= \cos{\theta} (\vec{v_\bot}) + \lVert v_\bot \rVert \sin{\theta} \frac{\vec{u}\times\vec{v_\bot}}{\lVert \vec{v_\bot} \rVert} \nonumber \\[10pt] &= \cos{\theta} (\vec{v_\bot}) + \sin{\theta} (\vec{u} \times \vec{v_\bot}) \label{ev3} \end{align}\]

이제 $\eqref{ev1}, \eqref{ev2}, \eqref{ev3}$을 종합하면 다음과 같다.

\[\begin{align} \vec{v'} &= \vec{v_\parallel} + \vec{v_\bot'} \nonumber \\[5pt] &= \vec{v_\parallel} + \cos{\theta} (\vec{v_\bot}) + \sin{\theta} (\vec{u} \times \vec{v_\bot}) \nonumber \\[5pt] &= \vec{v_\parallel} + \cos{\theta} ( \vec{v} - (\vec{u}\cdot\vec{v})\vec{u}) + \sin{\theta} (\vec{u} \times (\vec{v}-(\vec{u}\cdot\vec{v})\vec{u})) \nonumber \\ \nonumber \\[5pt] \vec{u} \times (\vec{v}-(\vec{u}\cdot\vec{v})\vec{u}) &= \vec{u} \times \vec{v} - \vec{u}\times\vec{u}(\vec{u}\cdot\vec{v}) \nonumber \\[5pt] &= \vec{u} \times \vec{v} \nonumber \\ \nonumber \\ \vec{v'} &= \vec{v_\parallel} + \cos{\theta} ( \vec{v} - (\vec{u}\cdot\vec{v})\vec{u}) + \sin{\theta} (\vec{u} \times \vec{v}) \nonumber \\[5pt] &= (\vec{u}\cdot\vec{v})\vec{u} + \cos{\theta} ( \vec{v} - (\vec{u}\cdot\vec{v})\vec{u}) + \sin{\theta} (\vec{u} \times \vec{v}) \nonumber \\[5pt] &= \vec{v} \cos{\theta} + \left(\vec{u} \times \vec{v} \right) \sin{\theta} + \vec{u} \left(\vec{u} \cdot \vec{v} \right)\left( 1 - \cos{\theta} \right) \end{align}\]

회전 행렬 형태 유도

벡터 를 행렬 형태로 표기할 땐 보통 세로로 표시한다. ($v = \begin{bmatrix} v_x & v_y & v_z\end{bmatrix}^T$)

벡터의 내적은 행렬 형태로 표시하면 다음과 같다.

\[\begin{align} \vec{a} \cdot \vec{b} = a^T b \end{align}\]

벡터의 외적은 행렬 형태로 표시하면 다음과 같다.

\[\begin{align} \vec{a} \times \vec{b} &= \left[ a\right]_\times b \\[5pt] [a]_\times &=\begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0\end{bmatrix}\\ \end{align}\]

참고 : Cross_product#Conversion_to_matrix_multiplication

저 외적 행렬 $[]_\times$는 반대칭 행렬(Skew-Symmetric Matrix), 외적 행렬(Cross Product Matrix)등으로 불린다.
반대칭 행렬의 정의는 $A^T = -A$이다.

이제 식 $\eqref{e1}$을 행렬 형태로 표현한 회전행렬 $R$은 다음과 같다.

\[\begin{align} v' &= cos{(\theta)} v + \sin{(\theta)} [u]_\times v + u^T v u \left( 1 - \cos{(\theta)} \right) \nonumber \\ &= \left[ \cos{(\theta)}I + \sin{(\theta)}[u]_\times + (1-\cos{\theta})uu^T \right]v \nonumber \\ &= Rv \nonumber \\ \\ \therefore R &= \cos{(\theta)}I + \sin{(\theta)}[u]_\times + (1-\cos{\theta})uu^T \label{e4} \end{align}\]

단위벡터 $\vec{u}$의 외적 행렬 $[u]_\times=K$에 대해 다음이 성립한다

\[\begin{align} u_x^2 + u_y^2 + u_z^2 = 1 \\ K^2 &= \begin{bmatrix} 0 & -u_z & u_y \\ u_z & 0 & -u_x \\ -u_y & u_x & 0 \end{bmatrix}\begin{bmatrix} 0 & -u_z & u_y \\ u_z & 0 & -u_x \\ -u_y & u_x & 0 \end{bmatrix} \nonumber \\[18pt] &= \begin{bmatrix} -u_z^2-u_y^2 & u_x u_y & u_x u_z \\ u_x u_y & -u_x^2-u_z^2 & u_y u_z \\ u_x u_z & u_y u_z & -u_x^2-u_y^2\end{bmatrix} \nonumber \\[18pt] &= \begin{bmatrix} u_x^2 & u_x u_y & u_x u_z \\ u_x u_y & u_y^2 & u_y u_z \\ u_x u_z & u_y u_z & u_z^2\end{bmatrix} - I \nonumber \\[18pt] \therefore K^2 &= uu^T - I \label{e5} \end{align}\]

이제 식 $\eqref{e4}$에 $\eqref{e5}$를 사용하면 다음과 같다.

\[\begin{align} R &= \cos{(\theta)}I + \sin{(\theta)}[u]_\times + (1-\cos{\theta})uu^T \nonumber \\[5pt] &= \cos{(\theta)}I + \sin{(\theta)}K + (1-\cos{\theta})(K^2 + I) \nonumber \\ \nonumber \\ \therefore R &= I + \sin{\theta} K + (1-\cos{\theta})K^2 \label{e6} \end{align}\]

위 식 $\eqref{e6}$의 형태가 좀 더 유명한데, Lie Group 중 $so(3)$의 Exponential을 취하면 나오는 형태이기 때문이다.

로드리게스 회전 변환 행렬의 형태를 총 정리하면 다음과 같다.

\[\begin{align} u &: \text{Unit rotation axis vector}\nonumber \\ \theta &: \text{Rotation angle} \nonumber \\ [u]_\times=K &: \text{Cross product matrix} \nonumber \\ \nonumber \\ R &= \cos{(\theta)}I + \sin{(\theta)}[u]_\times + (1-\cos{\theta})uu^T \nonumber \\[3pt] &= I + \sin{\theta} K + (1-\cos{\theta})K^2, \end{align}\]

이 방식의 장단점

장점

직관성
이러한 Axis-Angle 표현 방식은 상당히 직관적이다. 복잡하게 생각할 필요 없이, 공간상에 회전시킬 축과 회전할 각도만 있으면 빠르게 회전 행렬을 만들어 낼 수 있다.

이는 오일러 각(Euler Angle)이나 사원수(Quaternion)등의 표현 방식보다 더 직관적이다.

압축성
표현 방식에서 사용하는 숫자가 회전 행렬보다 적다. 축을 표현하는데에 필요한 3개의 숫자와, 회전각도 1개로 총 4개의 숫자만 있으면 되기 때문이다.

짐벌락 현상이 없다
오일러 각 방식과는 달리, 이 회전 표현 방식은 특정한 자세에서 회전 자유도를 잃어버리는 일이 없다. 어떤 자세이던지 원하는 방향으로의 각속도 벡터를 만들어 내기 위한 $\theta$와 $\vec{u}$를 결정할 수 있다.

단점

특이점의 존재

약간 어이없지만, $\theta=0$일때 $\vec{u}$가 정해지지 않으며, 이는 미분가능성에 잠재적인 위험이 있음을 의미한다.

식 $\eqref{e6}$를 살펴보면, $\theta=0$이면, 모든 $\vec{u}$ 항들을 전부 없애버리면서 $R=I$가 됨을 알 수 있다.
하지만 문제는 그 지점 근처에서는 $\frac{\partial R}{\partial u_x}$과 같은 parameter들의 편미분 값이 발산한다는 점이다. 이는 Gradient Vector의 수치적인 안정성을 크게 떨어트리며, Optimization 분야에서 사용하기 꺼려지게 만드는 원인이 된다.

정규화 문제
수학적으로는 지속적으로 계산하면서 더해도 문제가 없겠지만, 컴퓨터는 수치 에러가 누적되며 점점 $\vec{u}$의 길이가 1에서 벗어나게 된다.
따라서 매 프레임마다 u = u/u.norm() 등의 코드로 회전축 벡터를 정규화 시켜주어야 발산하지 않는다.

선형 보간 문제
2개의 회전(또는 자세) 사이의 보간에 있어서 이상하게 행동한다. 오일러각 표현법도 똑같이 공유하는 문제.

예를 들어, 2개의 자세 $\theta_1 \vec{u_1}=\vec{\theta_1}, \theta_2 \vec{u_2}=\vec{\theta_2}$가 있다고 하자. 첫번째 자세에서 2번째 자세로 가는 중간 자세는 어떻게 될까?

선형적으로 이를 보간하면 $\vec{\theta_m} = \large\frac{\vec{\theta_1} + \vec{\theta_2}}{2}$이 되지만, 실제로 이대로 해보면 영 이상한 회전 결과가 나온다.

왜냐하면 회전 보간의 본질적인 방법은 선형 보간(LERP)이 아니라 구면 보간(SLERP)이기 때문이다. 이는 쿼터니안 외에는 제대로 해결할 수 없는 문제이다. 축과 각도로 선형보간된 자세는 두 자세 사이를 부드럽게 전환시킬 수 없다.

합성 문제
여러개의 회전을 하나로 합성하는 방법이 꽤나 비직관적인 편에 속한다. 왜냐하면 결국 회전 행렬의 형태로 만들어야지만 회전을 합성할 수 있기 때문이며, 그 결과를 다시 회전축과 각도로 분리하는 것 역시 직관적이지 않다. 물론 쿼터니안은 이러한 문제가 없다.

각도 제한 문제
회전각 범위가 $\theta \in [0 ~ \pi)$로 제한된다. 왜냐하면 이 범위를 넘어서면, 정 반대 방향의 회전축과 범위가 겹치기 시작하기 때문이다. 즉, 하나의 자세를 표현하는 여러개의 결과가 생기게 된다.

계산 속도 문제
결국 실제로 점을 회전하려면 회전 행렬의 형태로 계산하는 것이 일반적이므로, 쿼터니안의 계산량보다 좀 더 많은 편에 속한다. 물론 오일러각 보단 적다.

로드리게스 회전의 장단점이라고 해놓고 쿼터니안을 홍보하는거 같은 느낌이 드는데,
정확하게 보셨다.