복소수의 Exponential Form과 극형식

복소수도 ‘수’ 이므로, 지수 형태를 정의할 수 있다.
어떤 형태가 되며 극형식과 어떤 관계가 있을까.

테일러 급수(Taylor Series)와 매클로린 급수(Maclaurin Series)

지수로써의 복소수를 이야기하기 전에, 전개 과정에서 필요한 부분을 먼저 짚고 넘어가려 한다.

지수함수는 초월함수지만, 우리가 복소수에 대해서 지금까지 정의한 부분은 대수 연산들 뿐이다(덧셈, 곱셈, 거듭제곱 등).
따라서, 초월함수를 대수 연산들로 분해할 수 있는 방법이 필요한데, 그 중 하나가 바로 테일러 급수(Taylor Series)이다.

위키피디아에 의하면 테일러 급수의 정의는 다음과 같다

무한히 미분 가능한 정칙 함수(Holomorphic function) $f:\mathbb{C} -> \mathbb{C}$ 및 복소수 $a \in \mathbb{C}$가 주어졌을 때,
$f$의 테일러 급수는 다음과 같은 멱급수이다.

\[\begin{align} f(x) &= f(a) + \frac{f'(a)}{1!}(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \cdots \\ &= \sum_{i=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n \end{align}\]

참고 : Taylor_series

이떄, $a=0$일 때의 급수를 특별히 매클로린 급수(Maclaurin Series)라 한다.
더욱 자세한 내용은 참고의 Taylor Series 부분을 보길 바란다.

테일러 급수를 통해서 다양한 초월함수들을 무한급수로 바꿀 수 있다.

유명한 몇개의 초월함수에 대한 매클로린 급수($a=0$인 테일러 급수)는 다음과 같다.

\[\begin{align} e^{x} &= 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots \label{e_ex} \\ \sin{x} &= \frac{x}{1!} - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \label{e_sin} \\ \cos{x} &= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots \label{e_cos} \\ \text{Converge at }\forall x \nonumber \end{align}\]

위의 급수 형태들을 눈에 익힌 뒤, 다음으로 넘어가자.

복소수의 Exponential Form

일단 냅다 e의 지수로 올려버리기

임의의 복소수 $z=a+bi, a,b \in \mathbb{R}$ 라 할때, 일단 냅다 $e^{a+bi}$를 생각해보자.
이는 다음과 같이 분해될 수 있다.

\[\begin{align} \large e^{a+bi} = e^a e^{bi} \nonumber \end{align}\]

우리는 이미 $e^a \in \mathbb{R}$임을 알고 있으므로, 별로 신기한 것은 아니다.
이제 우리의 관심은 대체 $e^{bi}$를 어떻게 해석할 것인지로 넘어간다.

테일러 급수와 오일러 등식

위에서 소개한 $e^{x}$의 매클로린 급수를 사용해 보자.

식 $\eqref{e_ex}$ ~ $\eqref{e_cos}$에 의하면, 다음과 같다.

\[\begin{align} e^{bi} &= 1 + \frac{bi}{1!} +\frac{(bi)^2}{2!} + \frac{(bi)^3}{3!} + \frac{(bi)^4}{4!} + \cdots \nonumber \\ &= 1 + \frac{bi}{1!} +\frac{-b^2}{2!} + \frac{-b^3i}{3!} + \frac{b^4}{4!} + \frac{b^5i}{5!} \cdots \nonumber \\ &= \left(1 -\frac{b^2}{2!}+ \frac{b^4}{4!} - \cdots \right) + i \left( \frac{b}{1!} - \frac{b^3}{3!} + \frac{b^5}{5!} - \cdots \right) \nonumber \\ &= \cos{b} + i\sin{b} \end{align}\]

이제 $\sin, \cos$에 걸맞게, $b$를 $\theta$로 바꿔보면 아주 유명한 등식이 등장한다.
바로 오일러 공식이다.

오일러 공식(Euler’s formula)

\[\begin{align} \large e^{\theta i} = \cos{\theta} + i \sin{\theta} \\ \text{if }\theta = \pi, e^{i \pi} + 1 = 0 \end{align}\]

오일러가 만든 공식들이 한두개도 아니고 엄청 많은데, 그 중에서도 ‘오일러 공식’ 이라는 이름을 차지할 정도로 유명하다.

Exponential Form과 극형식

오일러 항등식을 자세히 살펴보면, 재미있는 점이 보인다.
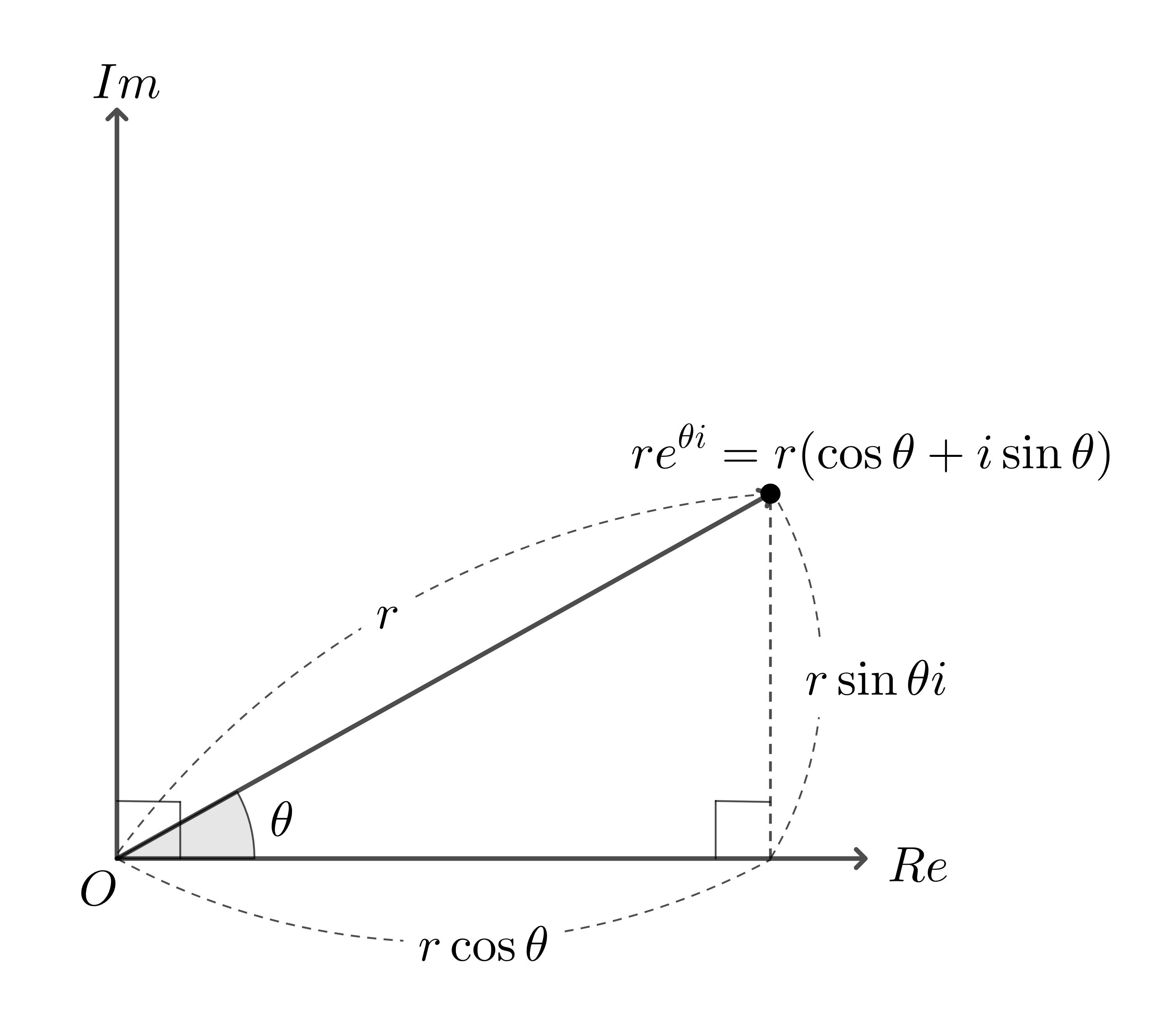
$e^{\theta i}$를 복소평면에 표시해보면 다음과 같다.

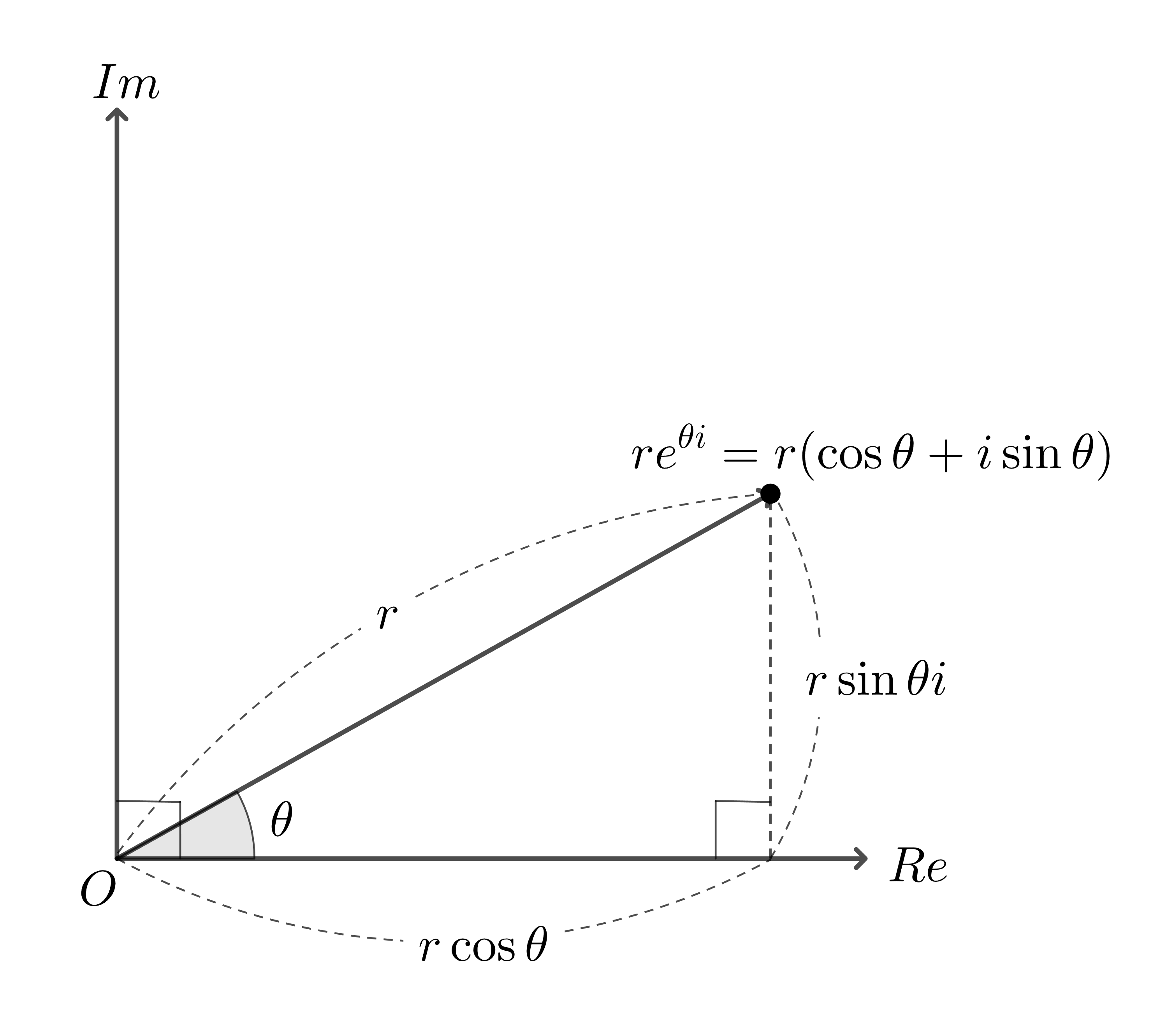그림 1 : 복소평면 상에서 복소수의 Exponential

이를 통해 다음의 성질을 확인할 수 있다.

복소수의 Exponential Form은 극형식과 다음의 관계가 있다.

\[\begin{align} \text{let } z = re^{\theta i}, \text{than} \nonumber\\ \left\vert z \right\vert = r \nonumber \\ arg(z) = \theta \end{align}\]

즉, 기존의 극형식이라고 부르던 것을 복소수의 지수 형태로 표현할 수 있음을 의미한다.
이를 통해 복소수 간의 곱셈이 의미하는 바를 더욱 명확하게 표현할 수 있다.

이제 길이가 $r_1, r_2$ 이고 편각이 $\alpha, \beta$인 복소수 $z_1, z_2$를 곱했을 때, 자연스러운 연산이 가능하다.

\[\begin{align} z_1 = r_1 e ^{\alpha}, z_2 = r_2 e^{\beta} \nonumber \\ z_1 \cdot z_2 = r_1 r_2 e^{(\alpha + \beta)} \end{align}\]

기존의 지수법칙이 동작하듯이, 마치 극형식으로 표현된 편각이 더해짐을 알 수 있다.

Exponential의 미분과 각속도

더욱 재밌는 점은 미분 역시 자유롭다는 점이다.

\[\begin{align} z = e^{\theta i} &= \cos{\theta} + i\sin{\theta} \nonumber \\ \frac{d}{dt}e^{\theta i} &= \frac{d}{dt}\left( \cos{\theta} + i\sin{\theta} \right) \nonumber \\ &= -\dot{\theta}\sin{\theta}+\dot{\theta} i \cos{\theta} \nonumber \\ &= \dot{\theta} i \left( \cos{\theta} + i \sin{\theta} \right) \nonumber\\ &= \dot{\theta} i \cdot e^{\theta i} \label{e1} \end{align}\]

기존에 $(e^x)’=x’ \cdot e^x$처럼 너무나 자연스럽게 일치한다.

조금만 더 나가면, 켤레복소수와의 관계도 생각해 볼 수 있다. \(\begin{align} \overline{e^{\theta i}} &= \overline{\cos{\theta} + i \sin{\theta}} \nonumber \\ &= \cos{\theta} - i \sin{\theta} \nonumber \\ &= \cos{(-\theta)} + \sin{(-\theta)} \nonumber \\ \therefore \overline{e^{\theta i}} &= e^{(-\theta i)} \end{align}\)

따라서 어떠한 복소수에 켤레복소수는 정확히 해당 복소수의 편각의 부호를 반전시킨 효과가 난다.

이제 기존의 $z \cdot \overline{z} = \left\vert z \right\vert^2$라는 결과도 Exponential로 해석하면 다음과 같다.

\[\begin{align} \text{let } z = r e^{\theta i}, \text{so } \left\vert z \right\vert = r \nonumber \\ z \cdot \overline{z} &= re^{\theta i} \cdot re^{-\theta i} \nonumber \\ &= r^2 \cdot e^{(\theta - \theta)i} \nonumber \\ &= r^2 \cdot e^{0i} = r^2 \nonumber \\ \therefore z \cdot \overline{z} &= \left\vert z \right\vert^2 \end{align}\]

서로 정 반대의 두 편각은 곱해지면서 사라지고, 실수부만 길이가 그대로 제곱되어 남는 것으로 해석할 수 있다.

이전에 $\left\vert z \right\vert = 1, arg(z) = \theta$인 자세 복소수 $z$에 대해서 각속도를 구했던 식은 다음과 같다.

\[\begin{align} \dot{z} \cdot \bar{z} &= \dot{\theta} i \end{align}\]

이제 각속도를 다시 Exponential Form을 통해 유도해 보면 다음과 같다.

\[\begin{align} \text {from }\eqref{e1}, \nonumber \\ \dot{z} &= \dot{\theta} i \cdot z \nonumber\\ \dot{z} \cdot \bar{z} &= \dot{\theta} i \cdot z \cdot \bar{z} \nonumber \\ &= \dot{\theta} i \end{align}\]

이제 평면의 회전과 자세를 수 하나로 표현할 수 있게 되었으며, 미분을 통해 각속도를 유도하는 것도 수학적으로 매끄러워졌다.

이 정도면 2차원의 자세에 대한 거의 모든것은 다 봤다고 봐도 무방하다.

다음 포스트부터는 3차원의 자세에 대해 시작할 예정이다.