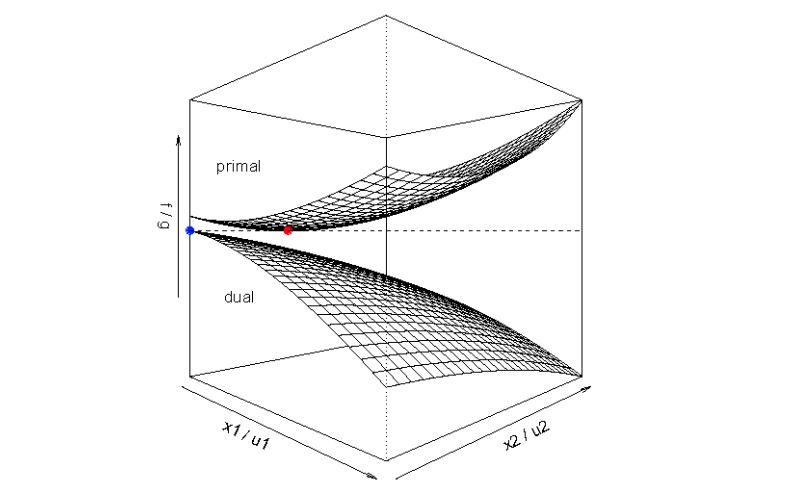
쌍대성(Duality)-Linear Programming

최적화 분야의 쌍대성(Duality)은 최적화 문제를 primal 문제와 dual 문제로 나누어서 생각하는 방법이다. 이번 포스트에서는 선형 프로그래밍(Linear Programming)에서의 duality에 대해 알아보도록 하자.

참고 1 : Duality (Optimization)
참고 2 : 모두를 위한 컨벡스 최적화, Duality in Linear Programs
참고 3 : CMU-convex optimiazation, Duality in Linear Programs

쌍대성(Duality)

최적화 이론에서 쌍대성(Duality)는 원래의 문제(Primal problem)과 관련된 형태의 다른 문제(Dual Problem)와의 성질이다. 문제에 따라 strong duality, weak duality를 가지며, strong duality의 경우 Primal과 dual 문제의 해가 같다.

이 성질은 여러가지 이유로 사용되는데,

• primal 문제를 직접 풀기 어렵거나 계산 비용이 높은 경우 dual 문제를 푸는 것이 더 쉬울 수 있다.
• strong duality라면 primal과 dual의 최적해의 값이 같다는게 보장 된다.
• 제약 조건 자체의 변화가 최적 해에 미치는 영향을 역으로 분석하는데에 dual problem이 사용될 수 있다.
• 일부 최적화 방법 (e.g. primal-dual interior-point method) 들은 primal 문제와 dual 문제를 동시에 사용하여 수렴 속도를 높인다.

$x \in \mathbb{R}^n, f : \mathbb{R}^n \rightarrow \mathbb{R}$과 등식 제약 조건 $g_i(x)=0, i=1 \cdots m$, 부등식 제약 조건 $h_j(x) \leq 0, j=1 \cdots p$를 가지는 최적화 문제를 생각해보자.

General Optimization Problem

\[\begin{align} \min_{x} & f(x) \\ \text{s.t. } & g_i(x) = 0, i=1 \cdots m \\ & h_j(x) \leq 0, j=1 \cdots p \end{align}\]

이제 이 문제를 쌍대성을 이용하여 다시 정의하면, 그때의 원래 문제(Primal Problem)와 쌍대 문제(Dual Problem)는 다음과 같이 정의된다 :

Primal Problem \(\begin{align} \min_{x} & \max_{u,v} \mathcal{L}(x,u,v) \\ \end{align}\) Dual Problem \(\begin{align} \max_{u,v} & \min_{x} \mathcal{L}(x,u,v) \\ \end{align}\)

$\mathcal{L}(x,u,v)$ : Lagrangian function \(\begin{align} \mathcal{L}(x,u,v) &= f(x) + \sum_{i=1}^{m} u_i g_i(x) + \sum_{j=1}^{p} v_j h_j(x), \\ &u \in \mathbb{R}^m, v \in \mathbb{R}^p, v_j \geq 0 \end{align}\)

이게 무슨 말인지 처음에는 도통 이해가 가지 않으니, 간단한 Linear Programming의 예시를 들며 천천히 알아보자.

Lower bound of simple LP

다음과 같은 간단한 예제를 생각해보자

함수 $f:\mathbb{R}^2 \rightarrow \mathbb{R}$와 $x,y \in \mathbb{R}$에 대해서 다음 최소화 문제가 있다 :

\[\begin{align} \min_{x,y} & f(x,y) = 2x + 3y \nonumber \\ \text{s.t.} & \text{ } x+y \geq 2 \nonumber \\ & x \geq 1, y \geq 0 \end{align}\]

이때, $\min_{x,y}f(x,y) \geq B$인 lower bound를 찾아보자.

\[\begin{align} &x + y \geq 2 \nonumber \\ + & x \geq 1 \nonumber \\ + & 2y \geq 0 \nonumber \\ \Rightarrow &2x + 3y \geq 3 = B \end{align}\]

각각의 부등식 제약(inequality constraint)에 상수배를 곱해서 더해서 원래 함수를 만들어 내면 동시에 lower bound도 찾을 수 있다.

이제 임의의 선형 결합으로 이뤄진 $f(x,y)$에 대해서도 lower bound를 찾을 수 있다.

\[\begin{align} \min_{x,y} & f(x,y) = px + qy, \quad p,q \in \mathbb{R} \nonumber \\ \text{s.t.} & \text{ } x+y \geq 2 \nonumber \\ & x \geq 1, y \geq 0 \end{align}\]

이때, $\min_{x,y}f(x,y) \geq B$인 lower bound를 찾아보자.
$a,b,c \in \mathbb{R}, \geq 0$에 대해서 :

\[\begin{align} &ax + ay \geq 2a \nonumber \\ + & bx \geq b \nonumber \\ + & cy \geq 0 \nonumber \\ \Rightarrow & (a+b)x + (a+c)y \geq 2a+b = B \end{align}\]

이를 lower bound $B$에 대한 문제로 바꾸면, 다음과 같다

\[\begin{align} \max_{a,b,c} & \text{ } B = 2a+b \nonumber \\ \text{s.t.} & \text{ } a+b = p \nonumber \\ & a+c = q \nonumber \\ & a,b,c \geq 0 \end{align}\]

위의 예제에서 눈여겨 볼 점은, 원래 문제를 최소화 시키는 것이, lower bound를 최대화 시키는 것과 같다는 점이다. 이때 원래 문제를 Primal Problem, lower bound에 대해 바뀐 문제를 Dual Problem이라고 부른다.

또한, 부등식 제약 조건의 경우, 부등식의 방향을 유지하기 위해 $a,b,c \geq 0$ 조건이 추가로 들어간다는 점도 기억하면 좋다.

Lower bound of General LP

이제 일반적인 Linear Programming 문제에 대해서 lower bound, $B$를 찾아보자.

$c \in \mathbb{R}^n, A \in \mathbb{R}^{m \times n}, b \in \mathbb{R}^m, G \in \mathbb{R}^{p \times n}, h \in \mathbb{R}^p$일 때,
다음과 같은 최소화 문제가 있다고 하자 :

\[\begin{align} \min_{x} & \text{ } c^Tx \nonumber \\ \text{s.t.} & \text{ } Ax = b \nonumber \\ & Gx \leq h \end{align}\]

이전과 동일하게 임의의 벡터 $u \in \mathbb{R}^m, v \in \mathbb{R}^p$를 사용해서 lower bound를 찾으면 다음과 같다 :

\[\begin{align} & u^T(Ax-b) = 0 \nonumber \\ + & v^T(Gx-h) \leq 0, \quad v \geq 0 \nonumber \\ = & u^TAx - u^Tb + v^TGx - v^Th \leq 0 \nonumber \\ \Rightarrow & \underbrace{-(u^TA + v^TG)}_{c^T}x \geq \underbrace{-u^Tb -v^Th}_B \end{align}\]

이를 Lower bound 에 대해 다시 정의하면 Dual Problem을 구할 수 있다 :

\[\begin{align} \max_{u,v} & \text{ } -u^Tb - v^Th \nonumber \\ \text{s.t.} & \text{ } -u^TA - v^TG = c^T \nonumber \\ & v \geq 0 \end{align}\]

Lagrangian Dual Problem

지금까지의 결과를 일반화한 Lagrangian Dual Problem을 유도해보자.

일단 위에서 General LP의 lower bound를 구하는 과정으로부터 다음 관계를 가진 lagrangian을 정의할 수 있다 :

Lagrangian Function of general LP

\[\begin{align} c^{T}x & \geq c^{T}x+\overbrace{u^{T} \underbrace{(Ax-b)} _ {=0}+\underbrace{v^{T}} _ {\geq 0} \underbrace{(Gx-h)} _ {\leq 0}} ^ {\leq 0} \nonumber \\ & := \mathcal{L}(x,u,v), \\ \nonumber \\ u &\in \mathbb{R}^m, \quad \text{lagrange mulpliers for eq constraints} \\ v &\geq 0, \in \mathbb{R}^p \quad \text{lagrange mulpliers for ineq constraints} \label{dual-lp-1} \end{align}\]

이 lagrangian은 $c^Tx \geq \mathcal{L}(x,u,v)$관계가 항상 성립한다. 이때, $v \geq 0$이어야만 함을 기억하자.

다음으로, 해가 존재하는 영역(feasible region) $D = {x: Ax=b, Gx \geq h}$과 primal 문제의 최적해, $x^*$ 에 대해서 원래 primal problem과 lagrangian은 다음의 관계를 가진다 :

\[\begin{align} f^* = f(x^* )=\min_{x\in D} f(x) \geq \min_{x\in D} \mathcal{L}(x,u,v) \geq \min_x \mathcal{L}(x,u,v):= \theta(u,v) \end{align}\]

$\ref{dual-lp-1}$에 의해서 첫번째 부등호가 성립하고, $x \in D$가 아니라면, 당연히 더 작은 값이 나올 수도 있으므로 두번째 부등호도 성립한다.

이때, $\theta(u,v)$를 dual function이라 하며, 원래 문제의 일종의 lower bound, $B$와 같은 역할을 한다.

이 값을 최대화 하도록 정의된 문제를 dual problem, 또는 lagrangian dual problem 이라 한다.

Lagrangian Dual Problem of general LP

\[\begin{align} \max_{u,v} & \text{ } \theta(u,v) = \max_{u,v} \min_{x} \mathcal{L}(x,u,v) \nonumber \\ \text{s.t.} & \text{ } v \geq 0 \nonumber \\ & -u^TA - v^TG = c^T \end{align}\]

이 방법은 LP 뿐만이 아니라, General Optimization Problem에 대해서도 적용 가능하다.