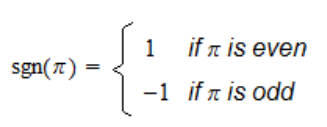순열의 부호
순열의 부호란 무엇이며, 어떤 성질이 있을까?
참고 1 : https://en.wikipedia.org/wiki/Parity_of_a_permutation
참고 2 : https://en.wikipedia.org/wiki/Alternating_group
참고 3 : https://dec41.user.srcf.net/notes/IA_M/groups.pdf
본 글은 $(\sigma \tau)(x) = \sigma(\tau(x))$ 표기를 사용합니다. 오른쪽이 먼저 작용합니다.
순열의 부호
순열의 부호(Parity of a permutation)는 하나의 순열이 가지는 고유한 특성 중 하나로, +1 또는 -1이다.
순열의 부호는 대칭군을 쪼개는 중요한 특성이며, 우리의 경우 슬라이딩 퍼즐의 해결 가능성과 큰 관련이 있다.
유한 대칭군 외에 일부 무한 대칭군도 순열의 부호를 정의할 순 있지만, 우린 거기까진 관심이 없으므로, 유한 대칭군에 대해서만 다루겠다.
일단 정의부터 먼저 보자 :
순열의 부호(Parity of a permutation)
$sgn(\sigma) = (-1)^{N(\sigma)}, \quad N(\sigma) \text{는 순열 }\sigma\text{의 반전의 수}$
여기서 반전(inversion)이란, 순열 $\sigma$에 대해 $i < j$ 이면서 $\sigma(i) > \sigma(j)$ 인 $(i, j)$ 쌍의 개수를 의미한다.또는, 다음과 같이 정의되기도 한다
$sgn(\sigma) = (-1)^m, \quad m$는 순열 $\sigma$을 두 원소의 교환(transposition)으로 나타낼 때 필요한 교환의 개수
즉, 순열의 부호는 그 순열이 짝수번의 반전을 가지는지 홀수번의 반전을 가지는지에 따라 결정되며, 동일하게 그 순열을 두 원소의 교환으로 나타낼 때 필요한 교환의 개수가 짝수인지 홀수인지에 따라서도 결정된다.
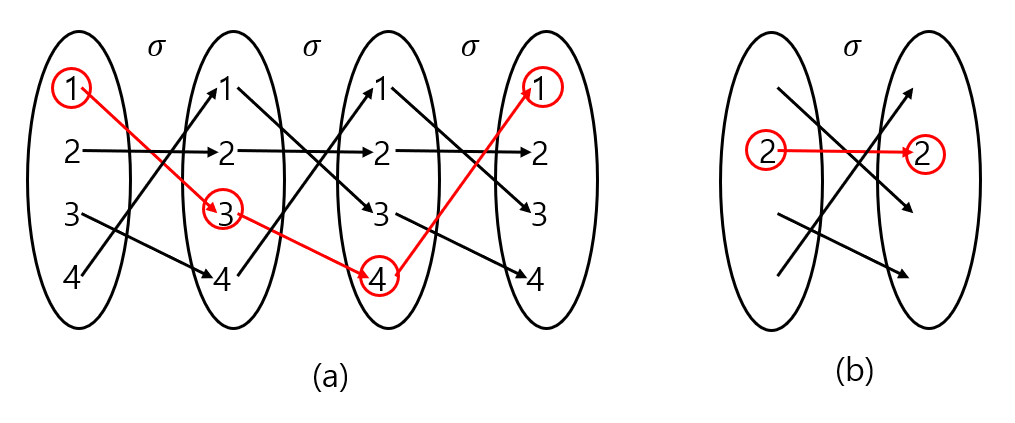
실제 순열, $ (2 \ 3 \ 4) \in S_4$를 예로 들어보자.
위 순열의 inversion의 수를 세 보면 다음과 같다 :
| i | j | $\sigma(i)$ | $\sigma(j)$ | $\sigma(i) > \sigma(j)$ ? | inversion? |
|---|---|---|---|---|---|
| 1 | 2 | 1 | 3 | X | X |
| 1 | 3 | 1 | 4 | X | X |
| 1 | 4 | 1 | 2 | X | X |
| 2 | 3 | 3 | 4 | X | X |
| 2 | 4 | 3 | 2 | O | O |
| 3 | 4 | 4 | 1 | O | O |
표 1 : 순열 (2 3 4) 의 inversion 개수 세기
따라서 \(N((2 \ 3 \ 4)) = 2\) 가 되므로, \(sgn((2 \ 3 \ 4)) = (-1)^2 = +1\) 이 되어 짝순열이 된다.
다음으로 두 원소의 교환(transposition)으로 나타낼 때 필요한 교환의 개수도 세어보자.
\[\begin{align} (2 \ 3 \ 4) &= (2 \ 3)(3 \ 4) \\ &= (3 \ 4)(2 \ 4) \\ &= (2 \ 4)(2 \ 3) \end{align}\]즉, 2번의 교환으로 가능하므로, \(sgn((2 \ 3 \ 4)) = (-1)^2 = +1\) 이 되어 짝순열이 됨을 알 수 있다.
그림으로 표현하면 다음과 같다.
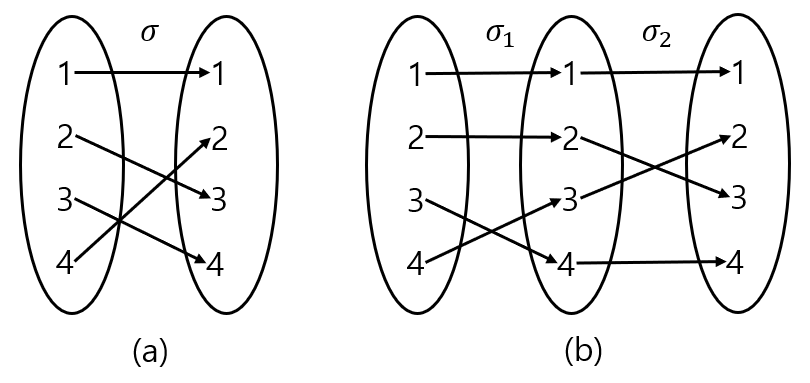그림 1 : (a) 순열 (2 3 4), (b) 두개의 transposition 으로의 분해 : (2 3)(3 4)
이제 이 사실이 과연 잘 성립하는지를 확인해보자
순열의 부호는 well-defined인가?
어떠한 정의가 잘 정의되었다(well-defined)는 것은, 그 정의가 모순 없이 일관되게 적용될 수 있음을 의미한다.
정의된 방식에 따라 결과가 항상 동일하게 나오는지를 확인하는 것이다.
즉, 순열의 정의에 따라, 모든 순열이 반드시 짝순열 또는 홀순열로 나뉠 수 있는지를 확인하는 것이다.
일단 inversion의 수에 따른 정의는 크게 의심할 여지가 없다.
- inversion의 수는 자연수이므로 반드시 짝수이거나 홀수 둘 중 하나임이 명확하다
- 어떤 순열이여도 inversion의 수는 반드시 존재한다. (최소 0개)
문제는 두 원소의 transposition으로 구성된 정의이다.
이거에 대해서는 inversion의 수에 따른 정의와, transposition에 따른 정의가 동일함을 보이는 것으로 충분하다.
inversion의 수와 transposition의 수
이제 inversion의 수와 transposition의 수가 동일함을 보이자.
즉, 어떤 순열 $\sigma$에 대해, $N(\sigma)$는 $\sigma$를 두 원소의 교환으로 나타낼 때 필요한 교환의 개수와 짝홀이 같다.
먼저, 어떤 순열 $\sigma$가 두 원소의 교환으로 나타낼 때 필요한 교환의 개수가 $m$,
$N(\sigma)$가 $\sigma$의 inversion의 수라고 하자.
[1] $\sigma$이 $m$개의 두 원소의 교환의 합성으로 나타낼 수 있다고 하자.
즉, \(\sigma = \tau_1 \tau_2 \cdots \tau_m\) 으로 분해하여 표현할 수 있다. 여기서 각 $\tau_i$는 어떤 두 원소의 교환이다.
[2] 인접한 두 원소의 교환은 inversion을 정확히 하나 변화시킴을 보이자.
먼저, 인접한 두 원소의 교환이란, \(\tau_i = (k \ k+1)\) 인 경우를 의미한다. 이때, $k$와 $k+1$에 대해 다음과 같은 두 가지 경우가 있다.
$\sigma(k) < \sigma(k+1)$ 인 경우
이 경우, $\sigma$에 대해 $(k, k+1)$ 쌍은 inversion이 아니다.
그러나, $\sigma \cdot \tau_i$에 대해, $(k, k+1)$ 쌍은 inversion이 된다.
즉, inversion의 수가 1 증가한다.$\sigma(k) > \sigma(k+1)$ 인 경우
이 경우, $\sigma$에 대해 $(k, k+1)$ 쌍은 inversion이다.
그러나, $\sigma \cdot \tau_i$에 대해, $(k, k+1)$ 쌍은 inversion이 아니다.
즉, inversion의 수가 1 감소한다.
[3] 인접하지 않는 두 원소의 교환은 inversion 수를 홀수개 변화시킴을 보이자.
이제, 인접하지 않는 두 원소의 교환, 즉 \(\tau_i = (a \ b), \quad a+1 < b\) 인 경우를 생각해보자. 이 경우, 다음과 같이 인접한 교환들의 곱으로 나타낼 수 있다 :
\[(a \ b) = (a \ a+1)(a+1 \ a+2) \cdots (b-2 \ b-1)(b-1 \ b)(b-2 \ b-1) \cdots (a+1 \ a+2)(a \ a+1)\]즉, 교환 $(a \ b)$는 $2(b-a)-1$개의 인접한 교환의 곱으로 나타낼 수 있다. 이는 홀수이므로, 교환 $(a \ b)$는 inversion의 수를 홀수개 변화시킨다.
[4] inversion의 수와 transposition의 수가 짝홀이 같다.
이제, $\sigma$가 $m$개의 두 원소의 교환의 곱으로 나타낼 수 있다고 하자.
각각의 두 원소의 교환은 inversion의 수를 홀수개 변화시키므로,
$m$개의 두 원소의 교환은 inversion의 수를 $m$번 홀수개 변화시킨다.
홀수를 짝수번 더하면 짝수, 홀수번 더하면 홀수가 되므로, $N(\sigma)$와 $m$은 짝홀이 같다.
disjoint cycle decomposition
사실 어물쩡 넘어갔지만, 우리가 짚지 않은 사실이 하나 있다. 정말 모든 순열은 두 원소의 교환들로 분해될 수 있냐는 게 그것이다.
물론, 반드시 분해할 수 있으며,
이를 증명하기 위해 순열의 disjoint cycle decomposition에 대해 알아보자.
disjoint는 ‘서로 겹치지 않는’ 이라는 뜻이다. 서로 겹치지 않는 순환표현들을 의미한다.
즉, 순열은 반드시 서로 겹치지 않는 순환표현(disjoint cycle representation)으로 분해될 수 있음을 의미한다.
이 분해의 정의는 다음과 같다 :
disjoint cycle representation
어떠한 순열 $\sigma$에 대해, $\sigma$를 다음과 같이 나타낼 수 있다. \(\sigma = (a_1 \ a_2 \ \cdots \ a_k)(b_1 \ b_2 \ \cdots \ b_m) \cdots (z_1 \ z_2 \ \cdots \ z_n)\) 여기서 각 싸이클이 서로 겹치지 않음을 의미한다. 즉, 각 싸이클의 원소 집합이 서로소이다.
즉, 어떠한 순열이여도 서로 겹치지 않는 순환표현들의 합성으로 나타낼 수 있음을 의미한다.
예를 들어, 다음과 같은 순열 $\sigma$가 있다고 하자.
\[\sigma = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 3 & 1 & 2 & 6 & 4 & 5 \end{pmatrix}\]이 순열을 disjoint cycle representation으로 나타내면 다음과 같다.
\[\sigma = (1 \ 3 \ 2)(4 \ 6 \ 5)\]각각의 싸이클이 서로 겹치지 않음을 알 수 있다.
증명
이러한 표현/분해가 항상 가능함을 증명하는 것은 비교적 간단한데,
마치 알고리즘처럼 순열의 원소들을 따라가며 싸이클을 형성하는 과정을 반복하면 된다.
먼저 어떤 유한집합 $X$를 섞는 순열 $\sigma$를 다음과 같이 정의한다 :
\[\sigma : X \rightarrow X, \sigma \text{ is bijective}\]이제 $X$의 원소 $x_1 \in X$를 하나 잡고, $\sigma$를 반복 적용하여 다음과 같은 집합을 정의한다 :
\[C_1 = \{ x_1, \sigma(x_1), \sigma^2(x_1), \ldots \}\]이 집합 $C_1$는 $x_1$을 시작으로 $\sigma$를 반복 적용하여 도달할 수 있는 모든 원소들의 집합이다.
$X$가 유한집합이므로, 언젠가는 $\sigma^k(x_1) = x_1$이 되는 $k$가 존재한다.
이제 $X^{(1)} = X \setminus C_1 \neq \emptyset$ 라면, $X^{(1)}$ 중에서 제일 작은 다음 원소, $x_2$를 잡고,
마찬가지로 다음과 같은 집합을 또 정의한다 :
이 집합 $C_2$는 $x_2$를 시작으로 $\sigma$를 반복 적용하여 도달할 수 있는 모든 원소들의 집합이다. 이 역시 유한 집합이다.
이렇게 구한 $C_2$를 또 $X^{(1)}$에서 빼고, 공집합이 아니라면 또 반복한다.
이 과정은 $X$가 유한집합이므로 언젠가 끝나게 된다.
그때의 $C = C_1 \cup C_2 \cup \cdots \cup C_n$ 각각이 서로 겹치지 않는 $n$개의 싸이클을 형성한다.
만약 항등 순열이었다면, 총 $n$개의 원소 각각이 자기 자신으로 가는 싸이클을 형성하는 식으로 끝난다.
결국, 이러한 과정을 통해 모든 순열은 disjoint cycle representation으로 나타낼 수 있음을 알 수 있다.
예시로, 어떤 순열 $\sigma$를 위 방법대로 분해하는 다음 그림을 보자 :
그림 2 : (a) 첫번째 싸이클 분해, (b) 두번째 싸이클 분해
transposition decomposition
거의 다 왔다.
이제 disjoint cycle representation을 통해 모든 순열은 transposition의 곱으로 나타낼 수 있음을 보이자.
여긴 엄청 간단한데, 임의의 n-cycle이 항상 n-1개의 transposition의 곱으로 나타낼 수 있기 때문이다 :
\[(a_1 \ a_2 \ \cdots \ a_n) = (a_1 \ a_2)(a_2 \ a_3) \cdots (a_{n-1} \ a_n)\]증명은 생략하겠다.
따라서, disjoint cycle representation으로 나타낸 순열 $\sigma$에 대해, 각각의 cycle을 transposition의 곱으로 또 나타낼 수 있으므로, 결국 모든 순열은 transposition의 곱으로 나타낼 수 있음을 알 수 있다.
transposition의 부호는 유일할까?
마지막 의심으로, transposition의 개수의 부호가 정말 유일한지 의심할 수 있다.
예를 들어, 어떤 순열을 분해했는데, 이리 저리 분해했더니 각각 짝수번과 홀수번의 transposition으로 나타낼 수 있다면 모순이 생긴다.
다행히도 그럴 수 없음을 이미 앞에서 보였다.
앞서 순열을 유한개의 transposition의 곱으로 나타낼 수 있다면, 그 개수의 짝홀이 반드시 inversion의 수의 짝홀과 같음을 보였다. 이제 inversion의 수는 순열의 고유한 특성이므로 , transposition의 개수의 짝홀 역시 순열의 고유한 특성이 된다.
직전에 순열을 유한개의 transposition의 곱으로 나타낼 수 있음까지 보였으므로,
모든 순열은 반드시 짝수 transposition 또는 홀수 transposition으로 나뉠 수 있으며, 그 부호는 유일하다 는 것을 알 수 있다.
교대군과 순열의 부호
재미있는 사실은, 짝순열들로만 이루어진 부분집합이 부분군을 이룬다는 것이다.
교대군(Alternating group)
$A_n = \{ \sigma \in S_n \mid sgn(\sigma) = +1 \}$
즉, 짝순열들로만 이루어진 $S_n$ 부분군
먼저 순열의 부호가 갖는 성질 하나를 알아보자 :
$sgn(\sigma \tau) = sgn(\sigma) \cdot sgn(\tau)$ for all $\sigma, \tau \in S_n$
이건 앞에서 해 놓은 게 많아서 아주 쉽다.
순열의 부호가 transpositon의 개수에 따라 결정되므로, \(sgn(\sigma) = (-1)^{m}, \quad sgn(\tau) = (-1)^{n}\) 이고, \(\sigma \tau\) 는 $m+n$개의 transposition의 곱으로 나타낼 수 있으므로, \(sgn(\sigma \tau) = (-1)^{m+n} = (-1)^m \cdot (-1)^n = sgn(\sigma) \cdot sgn(\tau)\) 이다.
이제 집합 $A_n = \{ \sigma \in S_n \mid sgn(\sigma) = +1 \}$ 가 부분군임을 보이자.
항등원
항등원 $e$에 대해, $sgn(e) = +1$ 이므로, $e \in A_n$ 이다.닫힘성
임의의 $\sigma, \tau \in A_n$ 에 대해, $sgn(\sigma \tau) = sgn(\sigma) \cdot sgn(\tau) = +1 \cdot +1 = +1$ 이므로, $\sigma \tau \in A_n$ 이다.역원
임의의 $\sigma \in A_n$ 에 대해, $sgn(\sigma^{-1}) = sgn(\sigma)^{-1} = +1^{-1} = +1$ 이므로, $\sigma^{-1} \in A_n$ 이다.
따라서, $A_n$은 $S_n$의 부분군임을 알 수 있다.
이 사실을 꼭 기억해 주자.
마치며
이번 포스팅은 순열의 부호가 무엇인지, 그리고 그것이 어떻게 잘 정의되는지를 살펴보았다.
왜 굳이 순열의 부호의 정의가 두 가지 버전이 있느냐 하면, 각각의 정의가 가지는 장단점이 있기 때문이다.
예를 들어 transposition의 개수로 된 정의는, 순열의 부호가 unique한지는 증명하기 힘들다.
반대로 inversion으로 된 정의는 순열의 부호가 갖는 성질을 증명하기 힘들다.
필요할 때마다 적절한 정의를 골라 쓰면 증명이 훨씬 쉽다. 두 정의가 동일함을 보였으니, 걱정 없이 필요할 때마다 골라 쓸 수 있다.
이제 필요한 모든 준비가 끝났다.
다음 포스팅부터 드디어 슬라이딩 퍼즐의 해결 가능성에 대해서 알아보겠다.