경사 하강법(Gradient descent)
최적화 기법 중에 제일 기본적이고 중요한 경사 하강법에 대해 소개한다.
참고 1 : Gradient Descent
참고 2 : 모두를 위한 컨벡스 최적화, Gradient Descent
참고 3 : CMU-convex optimiazation, gradient descent
경사 하강법(Gradient descent)
기본 개념
경사 하강법은 제약없는 1차 반복 알고리즘이며, 미분이 가능한 다변수 함수의 local minimum을 찾는 방법이다.
기본 수식은 다음과 같다 :
벡터 $x \in \mathbb{R}^n$과 다변수 함수 $f: \mathbb{R}^n \rightarrow \mathbb{R}$가 주어졌을 때, 초기점 $x_0$으로 부터 다음과 같이 반복한다
\[\begin{align} x_{i+1} = x_i - t \nabla f(x_i) \\ t \text{: step size} \end{align}\]
경사 하강법의 기본 아이디어는, 현재 위치에서의 그라디언트 벡터를 이용해 다음 위치를 찾아가는 것이다. 한 지점에서의 그라디언트 벡터는 해당 지점에서 함수값이 제일 가파르게 증가하는 방향을 나타낸다. 따라서 그 반대 방향으로 움직이면 함수값을 제일 빠르게 줄일 수 있다.
이 과정을 반복하면 근처에서 함수값이 제일 작은 구덩이로 수렴하게 되는데, 그곳이 시작점 근처의 local minimum이다.
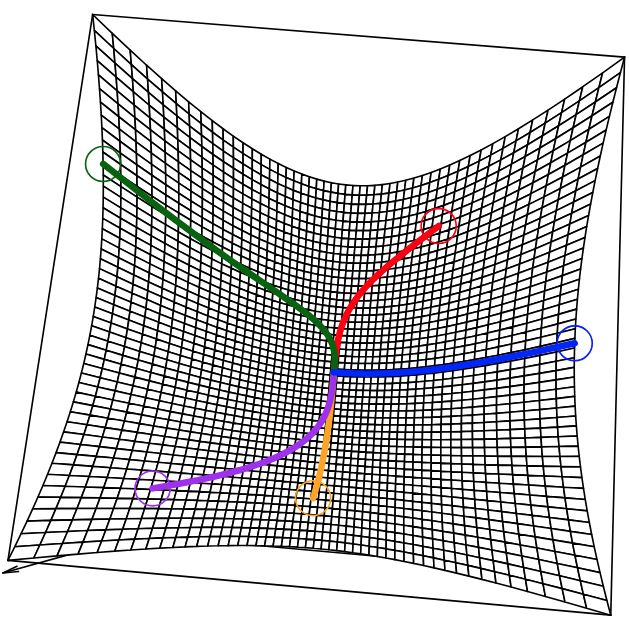
일반적인 비선형 최적화의 경우 다음처럼 근처의 local minimum으로 수렴한다.
nonlinear 목적함수의 경사 하강법. local minimum으로 수렴한다.출처
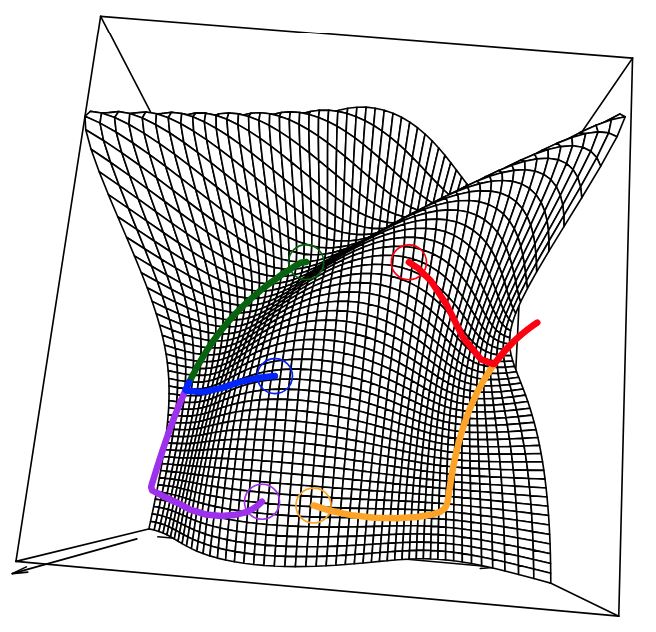
하지만 convex function의 경우, 단 하나의 local minimum이자 global minimum 밖에 없기 때문에 반드시 global minimum으로 수렴한다.
convex 목적함수의 경사 하강법. global minimum으로 수렴한다.출처
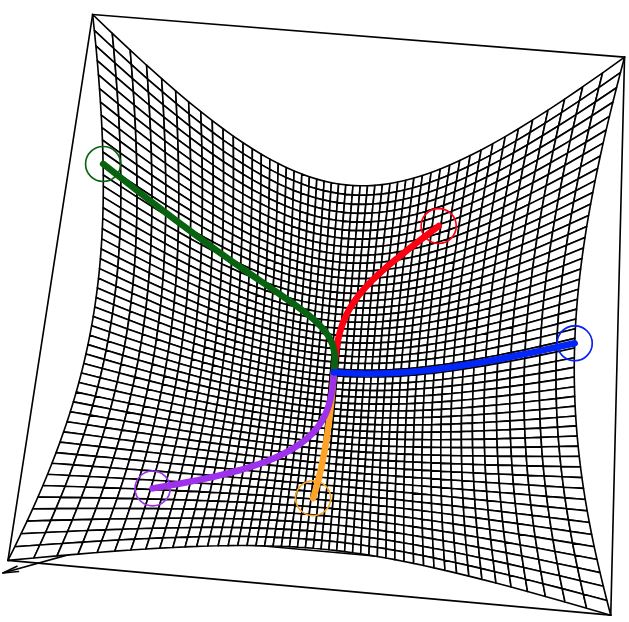
경사하강법은 특히 머신러닝 분야에서 많이 사용된다. 이때는 함수 $f$가 손실함수(loss function)이 되고, $x$는 모델의 파라미터가 된다.
경사하강법의 확장으로는 확률적 경사하강법(SGD, Stochastic Gradient Descent)이 있다. 이는 전체 데이터를 사용하는 것이 아니라, 랜덤하게 추출한 일부 데이터를 사용하여 그라디언트를 계산하는 방법이다. 이는 대용량 데이터를 다룰 때 효율적이며, 머신 러닝을 공부하면 바로 마주치게 되는 방법이다.
역사
경사 하강법은 수학자 코시(Augustin-Louis Cauchy)가 1847년 최초로 제안했다. 프랑스의 수학자 Jacques Hadamard도 비슷한 방법을 독립적으로 1907년에 제안했다.
1944년에 미국의 수학자 Haskell Curry가 비선형 최적화 문제를 해결하는 방법으로 처음 경사 하강법의 수렴 특성을 사용했고, 이후 10년 동안 많은 발전을 이뤘다.
경사 하강법의 해석
참고1 : 모두를 위한 컨벡스 최적화, Gradient Descent
참고2 : CMU-convex optimiazation, gradient descent
경사하강법은 다변수 함수의 2차 테일러 근사에서 유도할 수 있다.
다변수 함수의 테일러 전개 포스트에서, 다변수 함수의 2차 테일러 근사에 대해 다루었다.
다변수 함수 $f:\mathbb{R}^n \rightarrow \mathbb{R}$, 벡터 $x \in \mathbb{R}^n$에 대해서, 임의의 한 점 $x_0$ 근처에서 2차 테일러 근사는 다음과 같다 :
\[\begin{align} f(x) \approx f(x_0) + \nabla f(x_0)^T(x-x_0) + \frac{1}{2}(x-x_0)^T \nabla^2 f(x_0)(x-x_0) \end{align}\]이때, 헤시안 행렬 $\Delta^2 f$를 step size, $t$를 넣어서 $\frac{1}{t}I$로 바꾸면 다음과 같이 바뀐다.
\[\begin{align} f(x) \approx f(x_0) + \nabla f(x_0)^T(x-x_0) + \frac{1}{2t}||x-x_0||^2 \end{align}\]위 식에서 $f(x_0) + \nabla f(x_0)^T(x-x_0)$ $x_0$에서의 1차 테일러 근사항이며, $f(x)$에 접한 초평면(tangent hyperplane)이 된다. 뒤의 2차항, $\frac{1}{2t}\lVert x-x_0 \rVert$은 현재 지점과 $x$ 지점을 얼마나 근접시킬지에 대한 일종의 proximity term이 된다.
수정된 2차 테일러 근사식에서, $f(x)$를 최소화하는 지점 $x^+$를 찾으면 다음과 같다 :
\[\begin{align} \frac{\partial f}{\partial x} &\approx \nabla f(x_0) + \frac{1}{t}(x^+-x_0) = 0 \\[1em] \therefore x^+ &= x_0 - t \nabla f(x_0) \end{align}\]이는 경사하강법의 기본 형태와 동일하다.
Step size 선택 전략
step size는 경사하강법에서 정말 중요한 요소이다. 너무 작은 step size는 수렴 속도를 늦추고, 너무 큰 step size는 발산을 유발할 수 있다.
이에 다양한 방법이 개발되었는데, 크게는 fixed step size와 adaptive step size로 나눌 수 있다.
Fixed step size
스텝 사이즈를 정하는 제일 단순한 방법은 그냥 적당한 상수를 넣는 것이다. 단순하지만 계산이 빠르고 상황에 따라 잘 작동할 수 있다.
하지만 스텝 사이즈를 사전에 잘 정하지 않으면 수렴 속도가 저하되거나, 심지어 발산할 수도 있다.
다음은 함수 $f(x) = (10x_1^2 + x^2_2)/2$에 대해 fixed step size를 적용한 예시이다.
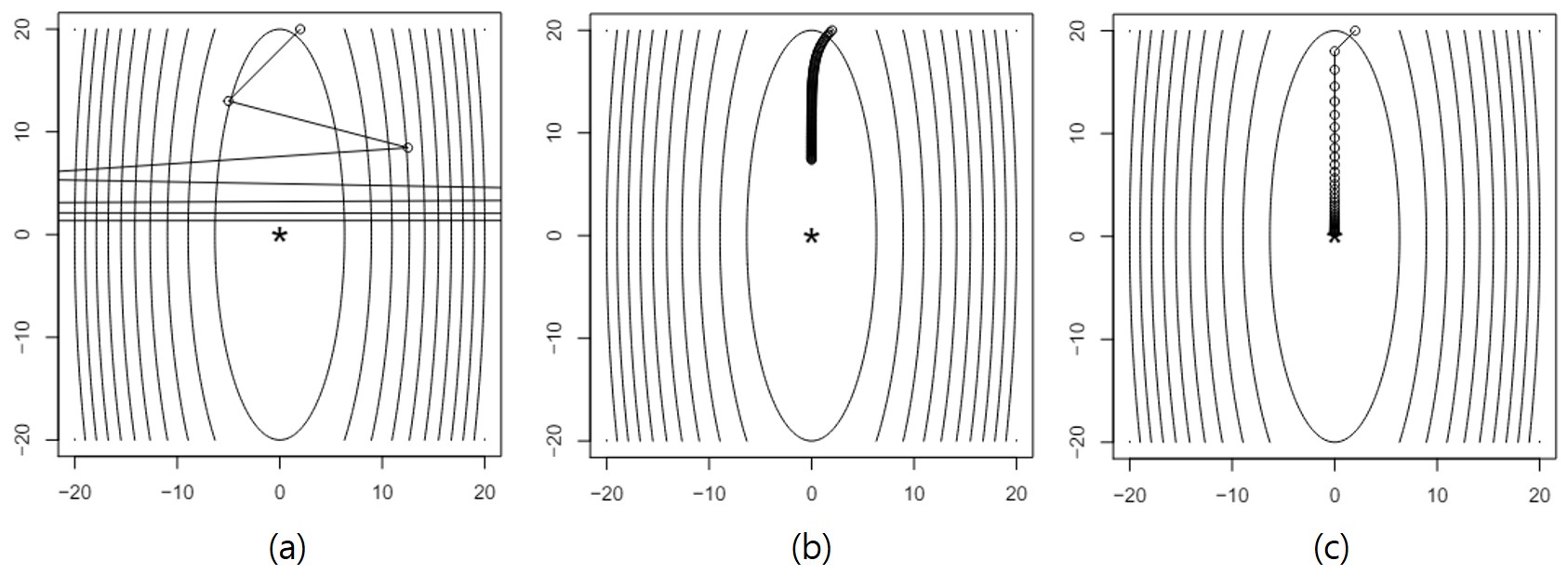step size에 따른 수렴 경로 차이. 출처
- (a)는 step size가 너무 커서, 지나치게 큰 이동 거리를 만들어 내며 아예 발산해 버린다.
- (b)는 step size가 너무 작아서, 100번의 반복을 해도 수렴하지 못했다.
- (c)는 step size가 딱 맞아서, 40번의 반복 후 수렴했다.
이때 딱 맞는 step size에 대한 내용은 수렴 분석(Convergence analysis)에서 다룬다. 이 포스트의 마지막에서 증명의 내용만 말하고, 자세한 증명 과정은 해당 페이지를 참고하자.
Exact line search
adaptive step size의 한 방법이며, 한 지점에서 그라디언트 방향으로의 step size를 밟았을 때, 목적함수의 값을 최소화 시키는 step size를 매번 계산하고 움직이는 방식이다.
step size를 정하는 방식은 다음과 같다 :
Exact line search
- 현재 위치 $x_i$에서 그라디언트 방향으로의 step size를 찾는다.
- $t = \arg \min_{t \geq 0} f(x_i-t\nabla f(x_i))$를 찾는다.
- $x_{i+1} = x_i - t\nabla f(x_i)$로 업데이트한다.
이 방법은 매우 정확하게 최적의 step size를 찾을 수 있지만, 2번 단계의 계산량이 너무 많아서 실제로는 잘 사용되지 않는다.
하지만 이 방법은 다른 방법들의 기반으로 사용되기 때문에 수식을 이해하는 것은 중요하다.
여기에서 $f(x_i-t\nabla f(x_i))$는 $t$에 대한 함수이며, $x_i$ 로부터 $-\nabla f(x_i)$방향으로 $t$만큼 움직였을 때의 함수값을 나타낸다. 이 함수를 최소화하는 최적의 $t$값, $ t^* $ 를 찾는 것이다.
예시로, 목적함수가 $x^2$인 경우에 대해서 살펴보자.
\[\begin{align} f(x-t\nabla f(x)) &= f(x-t(2x)) = f(x-2tx) = (x-2tx)^2 = x^2 - 4tx^2 + 4t^2x^2 \nonumber\\ \frac{d}{dt}f(x-t\nabla f(x)) &= -4x^2 + 8tx^2 = 0 \nonumber\\ \therefore t &= \frac{1}{2} \end{align}\]이제 아무 점 $(a,a^2)$으로부터 exact line search를 통해 최적의 step size 대로 움직여보면 다음과 같다 :
\[\begin{align} f(a - 0.5 (2a)) = f(0) \end{align}\]1변수 함수에다가 단순한 2차 함수를 적용했기 때문에, 한번에 정확한 스텝 사이즈로 수렴이 끝나는 모습이다.
Backtracking line search
Backtracking line search는 adaptive step size의 한 방법이다. 매 iteration 마다 step size를 동적으로 변화시키며 수렴을 더 빠르게 하도록 만든다.
기본적인 아이디어는 일단 적당히 큰 step size로 가본 다음, 괜찮다 싶을 때 까지 스텝 사이즈를 차근차근 줄여나가는 것이다.
이때, step size를 정하는 방법은 다음과 같다 :
Backtracking line search
- 초기 step size $t=t_0$, $\alpha \in (0,1)$, $\beta \in (0,1)$ 을 정한다.
보통 $\alpha = 0.5, \beta = 0.9$를 많이 사용한다.- 다음 식을 만족할 때까지 $t$를 줄인다.
- $f(x-t\nabla f(x)) \leq f(x) - \alpha t \lVert \nabla f(x) \rVert^2$를 만족할 때까지 $t$를 줄인다.
- $t$가 충분히 작아지면, $t$를 반환한다.
- 충분히 작아지지 않으면, $t$를 줄이고($t=\beta t$) 3번으로 돌아간다.
여기서 3번 절차의 부등식 형태를 유도해 보자.
앞서 exact line search에서 사용했던, $f(x_i + t\nabla f (x_i))$는 $t$에 대한 일변수 함수이다. $f$가 convex function 이라면, $t$에 따른 목적 함수의 함수값의 그래프는 다음과 같다 :
step size 에 따른 목적함수의 값 그래프. 출처
우리의 경우, $\Delta x = -\nabla f$이다.
step에 따른 진행 방향이 $-\nabla f(x_i)$이므로, 반드시 아래로 오목한 그래프를 그리게 된다.
임의의 step size $t$를 잡았을 때, 최적의 step size $ t^* $ 는 $f(x_i - t^* \nabla f(x_i))$가 최소가 되는 지점이다. 하지만 $ t^* $ 를 계산하는 것이 지나치게 복잡하므로, $t$를 일단 크게 잡고, $f(x_i - t \nabla f(x_i))$가 충분히 작아질 때까지 $t$를 줄여나가는 방식을 사용한다.
이때 $t$가 충분히 작아졌는지 어떻게 결정할 것인지가 핵심이다.
최적의 step size $ t^* $ 를 가진 지점을 $( t^* , f(x_i - t^* \nabla f(x_i))) = P$라고 하자.
$f(x+t\Delta x)$는 convex function 이므로, 나머지 모든 부분이 $(0,f(x_i))$의 접선보다 위에 있다. 이는 점 $P$ 역시 접선보다 위에 위치한다는 뜻이다. 해당 접선을 직접 구해보면 다음과 같다 :
그림에서 아래쪽 점선에 해당한다.
반대로 $(0, f(x_i))$를 지나면서 기울기가 0인 수평선을 그리면, 최적점 $P$는 반드시 그 아래에 있다. 해당 선의 방정식은 다음과 같다 :
\[\begin{align} y &= f(x_i) + 0 \cdot t = f(x_i) \end{align}\]그림에서 위쪽 점선에 해당한다.
이를 통해 알 수 있는 것은, (0 ~ 접선의 기울기) 사이인 직선과의 교점이 최적점 $P$와 좀 더 근접하다는 것이다. 그 사이의 기울기를 가진 선이 그림에서 가운데 점선에 해당하며, $\alpha\nabla f^T \Delta x$ $(\alpha \in (0,1))$의 기울기를 가진 선이 된다.
이제 Gradient descent 방법에서는 $\Delta x = - \nabla f(x)$임을 이용해서 그 선을 직접 구해보면 다음과 같다 :
\[\begin{align} y &= f(x_i) + \alpha \nabla f(x_i)^T \Delta x t \nonumber \\ &= f(x_i) - \alpha t \nabla f(x_i)^T \nabla f(x_i) \nonumber \\ &= f(x_i) - \alpha t \lVert \nabla f(x_i) \rVert^2 \end{align}\]3번 절차의 부등식의 우변에 등장하는 수식이 된다.
그림에서 보듯이 $\alpha$배의 기울기를 가진 직선과의 교점에서의 step size가 $t_{\alpha}$이다. 이제 backtracking line search를 다르게 설명해보면,
Backtracking line search
- 초기 step size $t$를 정한다, $\alpha \in (0,1)$, $\beta \in (0,1)$ 을 정한다.
보통 $\alpha = 0.5, \beta = 0.9$를 많이 사용한다.- $t \leq t_{\alpha}$이면 그대로 종료한다.
- $t > t_{\alpha}$이면, $t=\beta t$로 줄이고 다시 2번으로 돌아간다.
를 하는 것임을 이해할 수 있다.
Convergence Analysis
수렴 분석은 경사하강법의 수렴 속도를 분석하는 것이다.
이때 함수 $f$가 convex 하고, differentiable 하고, $\nabla f$가 Lipschitz continuous 하며, 그때의 Lipshitz constant 가 $L$ 임을 가정한다.
Lipshitz continuous는 어떤 함수 $g(x)$가 다음과 같은 조건을 만족할 때를 말한다.
Lipschitz continuous
\[\begin{align} \lVert g(x) - g(y) \rVert_2 \leq L \lVert x - y \rVert_2, L \geq 0 \end{align}\]$L$ : Lipschitz constant
쉽게 말하면, 두 점 사이의 기울기를 일정 크기 이상으로 증가시키지 않는 함수이다. 기울기의 크기에 상한이 있다고 생각하면 된다.
참고 : Lipschitz continuity
이때 경사하강법은 fixed step size $t \leq 1/L$ 에서 다음과 같은 속도로 수렴한다.
\[\begin{align} f(x_k) - f(x^*) \leq \frac{\lVert x_0 - x^* \rVert^2_2}{2tk} \end{align}\]
backtracking line searching를 했을 땐 다음과 같은 속도로 수렴한다
\[\begin{align} t_{min} &= \min{(1, \beta / L)} \nonumber \\ f(x_k) - f(x^*) &\leq \frac{\lVert x_0 - x^* \rVert^2_2}{2 t_{min} k}, t_{min} = \min{(1, \beta / L)} \end{align}\]
위 두 정리에 대한 자세한 유도 과정은 다음을 참고하자