군의 정의와 기본 성질들

군이란 무엇이고 어떤 기본 성질이 있을까?

참고 1 : https://en.wikipedia.org/wiki/Group_(mathematics)#
참고 2 : https://dec41.user.srcf.net/notes/IA_M/groups.pdf

서론

슬라이딩 퍼즐의 해결 가능성 문제를 군론을 통해 접근하려면, 군론의 기초 개념들과 문제 해결에 필요한 최소한의 성질들을 알아야 한다. 군론은 대수학의 한 분야, 그 중에서도 추상 대수학의 한 분야이다. ‘추상’ 이라는 단어가 붙은 만큼 그림이 아예 필요 없는 건 아니지만, 그림보다는 수식과 논리적인 설명이 훨씬 더 많이 등장할 것이다.

군이란 무엇인가

군론의 가장 기본적인 개념은 바로 군(group)이다.

이하 군의 정의는 다음과 같다.

다음 성질들을 만족하는 집합 $G$와 이항 연산 $\cdot$의 쌍,

1. 폐쇄성(Closure) : 임의의 $a, b \in G$에 대해, $a \cdot b \in G$이다.
2. 결합법칙(Associativity) : 임의의 $a, b, c \in G$에 대해, $(a \cdot b) \cdot c = a \cdot (b \cdot c)$이다.
3. 항등원(Identity element) : $e \in G$가 존재하여, 임의의 $a \in G$에 대해, $e \cdot a = a \cdot e = a$이다.
4. 역원(Inverse element) : 임의의 $a \in G$에 대해, $b \in G$가 존재하여, $a \cdot b = b \cdot a = e$이다.

을 만족할 때, $(G, \cdot)$를 군이라고 한다.

여기서 이항 연산이란 두 원소를 하나의 원소로 대응시키는 연산을 의미한다.
예를 들어, 덧셈, 곱셈 등이 있지만, 어떤 연산이든 두 원소를 하나의 원소에 대응시키기만 하면 전부 이항 연산이 된다.

군의 예시, 그리고 직관

갑자기 정의를 다다닥 나열하니 잘 와닿지 않을 수 있으므로, 간단한 예시를 통해 살펴보자.
군의 제일 단순한 예로는, 회전에 대한 대칭이 있을 것이다.

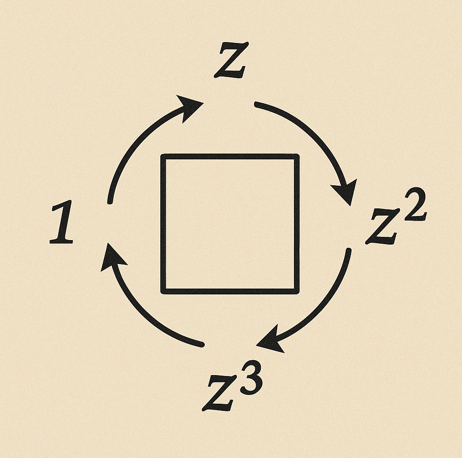
그림과 같은 4개의 꼭짓점을 가진 정사각형의 형태를 보존하면서 꼭지점의 위치를 바꾸는 회전이다. 각각 0도, 90도, 180도, 270도 회전이 가능하다.

물론 360도 회전이나 -90도 회전도 가능하나, 이는 각각 0도 회전과 270도 회전으로 대체할 수 있으므로 굳이 따로 고려하지 않는다.

그림 1 : 정사각형의 회전 군

회전을 표현하는 제일 단순한 방법은 복소수를 사용하는 것이다. 복소수의 곱셈 연산을 사용해서 $z=i$일 때, 각각의 회전을 이렇게 표현해 보자 :

• $z^0 = 1$ : 0도 회전
• $z^1 = i$ : 90도 회전
• $z^2 = -1$ : 180도 회전
• $z^3 = -i$ : 270도 회전

$\therefore G = \{ 1, z^1, z^2, z^3 \}$

이제 이 회전들의 집합이 군의 정의를 만족하는지 살펴보자.

1. 폐쇄성(Closure)
   군의 모든 원소 $a, b \in G$에 대해, $a \cdot b \in G$이어야 한다. 우리가 정의한 집합에서, $z^4 = z^0 = 1$ 이며. $z^5 = z^4 \times z^1 = 1 \times i = z^1$이 된다.
   즉, $z^n, z^m \in G, n,m \in \mathbb{Z}$에 대해, $z^{n+m} \in G$이 되므로 폐쇄성을 만족한다.

2. 결합법칙(Associativity)
   군의 모든 원소 $a, b, c \in G$에 대해, $(a \cdot b) \cdot c = a \cdot (b \cdot c)$이어야 한다. 복소수의 곱셈은 결합법칙을 만족하므로, 이 조건도 만족한다.

3. 항등원(Identity element)
   군의 원소 $e \in G$가 존재하여, 임의의 $a \in G$에 대해, $e \cdot a = a \cdot e = a$이어야 한다. 우리가 정의한 집합에서, $z^0 = 1$이 항등원 역할을 하므로 이 조건도 만족한다.

4. 역원(Inverse element)
   군의 모든 원소 $a \in G$에 대해, $b \in G$가 존재하여, $a \cdot b = b \cdot a = e$이어야 한다. 우리가 정의한 집합에서, 각 원소의 역원은 다음과 같다 :

   • $1$의 역원은 $1$
   • $z^1$의 역원은 $z^3$
   • $z^2$의 역원은 $z^2$
   • $z^3$의 역원은 $z^1$

즉 저 회전들의 집합은 군의 정의를 만족하므로, 비로소 군이 된다.

군의 핵심은 원소 간의 관계

재미있는 사실은, 굳이 저런 표기를 사용할 필요가 없다는 것이다.
원소도, 연산도 아무렇게나 표기해도 상관 없다.

저 정사각형의 회전에 대한 집합을 $G$ 라고 하고, 각각의 회전을 다음과 같이 표기해 보자 :

• $a$ : 0도 회전
• $b$ : 90도 회전
• $c$ : 180도 회전
• $d$ : 270도 회전

그리고 회전들을 합성하는 연산을 $\cdot$ 라고 하면, $(G, \cdot) = (\{ a, b, c, d \}, \cdot )$는 군이 된다.
이게 위의 복소수 표기로 이루어진 군과 완벽하게 동일해지려면, 한가지만 더 만족하면 된다.

바로 연산 구조가 같아야 한다는 것이다.

어떤 이항 연산의 모든 연산 결과를 표로 정리한 것을 연산표라 하며,
그게 다음과 같아야 위의 복소수 표기로 이루어진 군과 동일한 군이 된다 :

$\cdot$	$a$	$b$	$c$	$d$
a	a	b	c	d
b	b	c	d	a
c	c	d	a	b
d	d	a	b	c

표 1 : 군 $G$의 연산표

이렇게 정의해도 위의 복소수 표기로 이루어진 군과 완벽하게 동일한 결과가 나온다.
핵심은, 원소를 어떻게 표기하느냐가 아니라 그 원소들이 연산에 대해 어떤 관계를 가지느냐이다.

즉 군이 진짜 관심 있는 것은 원소들 간의 관계이다.

표현법에 대해서는 군의 표현론(Representation Theory)이라는 분야가 따로 있다고 하나, 거기까진 필자가 잘 모르니 넘어가도록 하자.

여담으로, 이 군은 순환군(Cyclic Group)이라고 불리며, 원소 n개짜리 순환군은 보통 $C_n$으로 표기한다. 이 경우에는 원소가 4개이므로 $C_4$라고 부른다.

순환군의 재미있는 특징으로, 무려 교환법칙(Commutativity)을 만족한다는 점이 있다. 즉, 임의의 $a, b \in G$에 대해, $a \cdot b = b \cdot a$가 성립한다.

결합법칙은 군의 정의에 의해 보장되지만, 교환법칙까지 보장하진 못한다.
그래서 교환법칙이 성립하는 군을 특별히 가환군, 또는 아벨군(Abelian Group)이라고 부른다.

항등원은 유일한가?

항등원이라는 말을 들어본 세대도 있고, 들어보지 못한 세대도 있을 것이다.

만약 항등원을 중학교 때 배웠던 세대라면, 항등원의 정의에 대해 다음과 같이 기억할 것이다 :

임의의 $a$에 대해, $e \cdot a = a \cdot e = a$인 원소 $e$를 항등원이라고 한다.

즉 항등원은 어떤 원소와 연산을 해도 그 원소가 그대로 나오는 원소이다.

만약 항등원을 중학교 때 배우지 않은 젊은 세대여도, 행렬의 항등 행렬(Identity Matrix)를 통해 항등원의 개념을 이해할 수 있을 것이다.

왜냐하면 $n$차원 정사각행렬의 집합이 곱셈에 대해 군을 이룬다는걸 쉽게 떠올릴 수 있고,
그 때 항등원이 바로 $I$, 항등행렬이기 때문이다 :

\[\begin{align} \forall A \in \mathbb{R}^{n \times n}, \\ I \cdot A = A \cdot I = A \end{align}\]

그런데, 항등원은 정말 유일할까?

되게 어이없는 의문처럼 들릴 수도 있다.
왜냐하면 $\mathbb{R}^{n \times n}$의 모든 원소에 대해 항등원은 얼핏 생각해봐도 $I$ 하나뿐이기 때문이다.

하지만 군의 정의 그 어디에도 항등원이 유일하다는 말은 없다. 정말 항등원은 그 군에 단 하나만 존재할까?

항등원 유일성의 증명

그 어떠한 군이여도 항등원은 유일하다. 증명해 보자.

임의의 군 $(G, \cdot)$에서, $e_1, e_2 \in G$가 각각 항등원이라고 하자.
그러면 임의의 $a \in G$에 대해, \(\begin{align} e_1 \cdot a &= a \cdot e_1 = a \label{eq:identity1}\\ e_2 \cdot a &= a \cdot e_2 = a \label{eq:identity2} \end{align}\) 가 성립한다.
이제 \eqref{eq:identity1}과 \eqref{eq:identity2}의 $a$에 각각 $e_2$와 $e_1$을 대입하면, \(\begin{align} e_1 \cdot e_2 &= e_2 \label{eq:identity3}\\ e_2 \cdot e_1 &= e_1 \label{eq:identity4} \end{align}\) 가 성립한다.

따라서 $e_1 = e_2$이므로, 항등원은 $e$로 유일하다.

즉 어떠한 군이여도 항등원은 유일하다.
안심하고 항등원을 $e$라는 원소로 표기하자.

역원은 유일한가?

역원이라는 말 역시 들어본 세대도 있고, 들어보지 못한 세대도 있을 것이다.

역원 역시 중학교 때 배웠던 세대라면, 역원의 정의에 대해 다음과 같이 기억할 것이다 :

임의의 $a$에 대해, $a \cdot b = b \cdot a = e$인 원소 $b$를 $a$의 역원이라고 한다.

또는 아까와 같이 정방행렬의 역행렬(Inverse Matrix)을 통해 역원의 개념을 이해할 수 있을 것이다.

\[\begin{align} \forall A \in \mathbb{R}^{n \times n}, A \cdot A^{-1} = A^{-1} \cdot A = I \end{align}\]

이제 역원도 유일한지 궁금해진다. 일단 행렬로 생각해 보면, $A$의 역행렬은 $A^{-1}$로 유일하다.
그렇다면 더 확장해서 어떠한 군이여도 역원은 유일할까?

역원 유일성의 증명

역원 역시 어떠한 군이여도 유일하다. 증명해 보자.

임의의 군 $(G, \cdot)$에서, $a \in G$에 대해 $b_1, b_2 \in G$가 각각 $a$의 역원이라고 하자. 그러면, \(\begin{align} a \cdot b_1 &= b_1 \cdot a = e \label{eq:inverse1}\\ a \cdot b_2 &= b_2 \cdot a = e \label{eq:inverse2} \end{align}\) 가 성립한다.

이제 다음 등식을 살펴보자.

\[\begin{align} b_2 \cdot (a \cdot b_1) &= (b_2 \cdot a) \cdot b_1 \nonumber \\ \therefore b_2 \cdot e &= e \cdot b_1 \nonumber \\ \therefore b_2 &= b_1 \label{eq:inverse3} \end{align}\]

따라서 $b_1 = b_2$이므로, 역원은 $b$로 유일하다.

우리는 군의 정의에 명시된 결합법칙과 항등원의 정의만을 사용했다.
즉, 어떠한 군이여도 역원은 유일하다.

통상 역원을 $a^{-1}$로 표기한다.

Cancellation Property

앞에서 항등원과 역원이 유일함을 군의 정의로부터 증명했다.
즉, 군이기만 하면 자동으로 항등원과 역원이 유일하다는 뜻이다.

그 덕분에 군이 가지는 또 하나의 중요한 성질을 증명할 수 있는데, 바로 Cancellation Property이다.

Cancelltation Property

군 $(G, \cdot)$에서, 임의의 $a, b, c \in G$에 대해,

• $a \cdot b = a \cdot c \Rightarrow b = c$
• $b \cdot a = c \cdot a \Rightarrow b = c$ 가 성립한다.

증명은 앞의 두 성질을 사용하면 아주 간단하다.

\[\begin{align} a \cdot b &= a \cdot c \nonumber \\ \therefore a^{-1} \cdot (a \cdot b) &= a^{-1} \cdot (a \cdot c) \nonumber \\ \therefore (a^{-1} \cdot a) \cdot b &= (a^{-1} \cdot a) \cdot c \nonumber \\ \therefore e \cdot b &= e \cdot c \nonumber \\ \therefore b &= c \end{align}\]

즉, 어떠한 군이여도 Cancellation Property를 만족한다.

이는 $a$에 대한 $a^{-1}$이 유일하므로, 양 변에 항상 같은 원소를 곱해줄 수 있기 때문이다. 이후 그렇게 등장하는 항등원의 정의에 의해 양 변이 같아지므로, 결국 $b=c$가 된다.

이 성질은 당연한 것 같아도, 절대 당연하지 않다.
역원이 존재하지 않거나, 유일하지 않은 경우에는 성립하지 않기 때문이다.

예를 들어, $n$차 정방행렬의 집합 $\mathbb{R}^{n \times n}$에는 역행렬이 존재하지 않는 행렬들이 존재한다. 따라서 행렬의 곱셈에 대해 군이 되지 않으며, 결과적으로 Cancellation Property도 성립하지 않는다.

예시로 다음과 같은 행렬들을 생각해 보자.

\[\begin{align} A = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}, \quad B = \begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix}, \quad C = \begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix} \end{align}\]

그러면 $A \cdot B = A \cdot C = 0$이지만, $B \neq C$이다.

물론 역행렬이 존재하는 $n$차 정방행렬의 집합 $GL(n)$에 대해서는 Cancellation Property가 성립한다.

\[\begin{align} \forall A, B, C \in GL(n), \nonumber \\ A \cdot B &= A \cdot C \nonumber \\ A^{-1} \cdot (A \cdot B) &= A^{-1} \cdot (A \cdot C) \nonumber \\ (A^{-1} \cdot A) \cdot B &= (A^{-1} \cdot A) \cdot C \nonumber \\ I \cdot B &= I \cdot C \nonumber \\ B &= C \end{align}\]

당연하게도 $GL(n)$ 자체가 군이기 때문이다.

반대로 어떤 집합과 연산에 대해서 Cancellation Property가 성립하지 않는다면, 그게 군을 이루지 않는다는 사실도 눈치챌 수 있다.

군의 크기

군의 크기, 즉 원소의 개수를 군의 차수/위수(Order)라고 한다.

물론 군의 차수가 유한할 수도 있고, 무한할 수도 있다. 방금 살펴본 $C_4$는 원소가 4개이므로 유한군이며, $GL(n)$은 원소가 무한히 많으므로 무한군이다.

다행히 우리는 슬라이딩 퍼즐의 해결 가능성 문제를 다루기 위해 유한군만 알면 된다.

통상 군의 차수는 다음과 같이 표기한다 :

\[|G| := \text{군 } G \text{의 차수} := \text{집합 } G \text{의 원소 개수}\]

마무리

군의 정의와 항등원, 역원의 유일성에 대해 알아보았다.

다음 포스트에서는 군의 부분집합이 또 군이 되는, 부분군(Subgroup)에 대해 포스팅하겠다.