2차원 회전 변환의 단순한 유도

간단하게 고등 교과 과정의 삼각함수 합 공식을 사용하여 2차원 회전 변환을 유도해본다.

삼각함수를 사용하여 유도

그림1

그림2

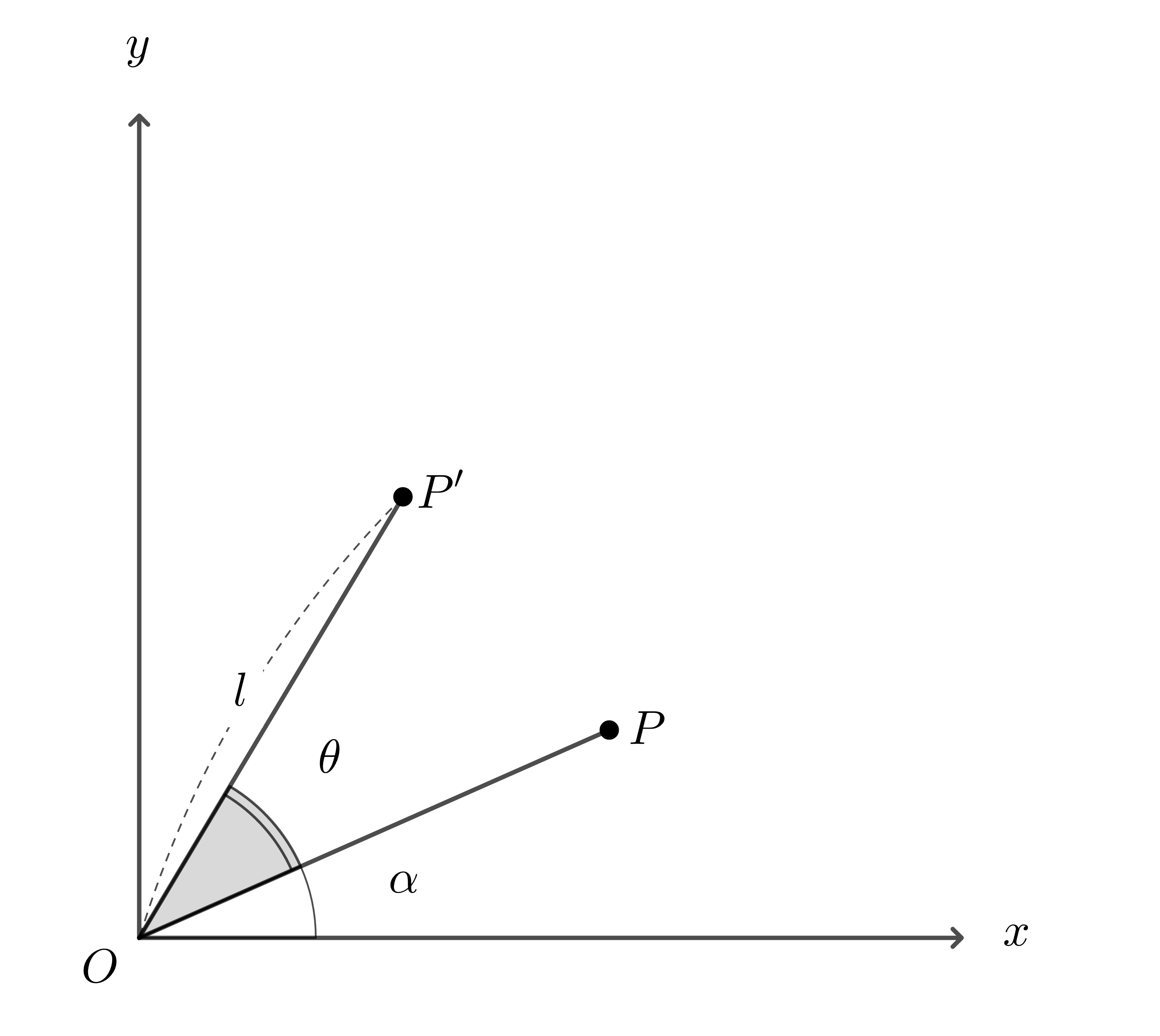
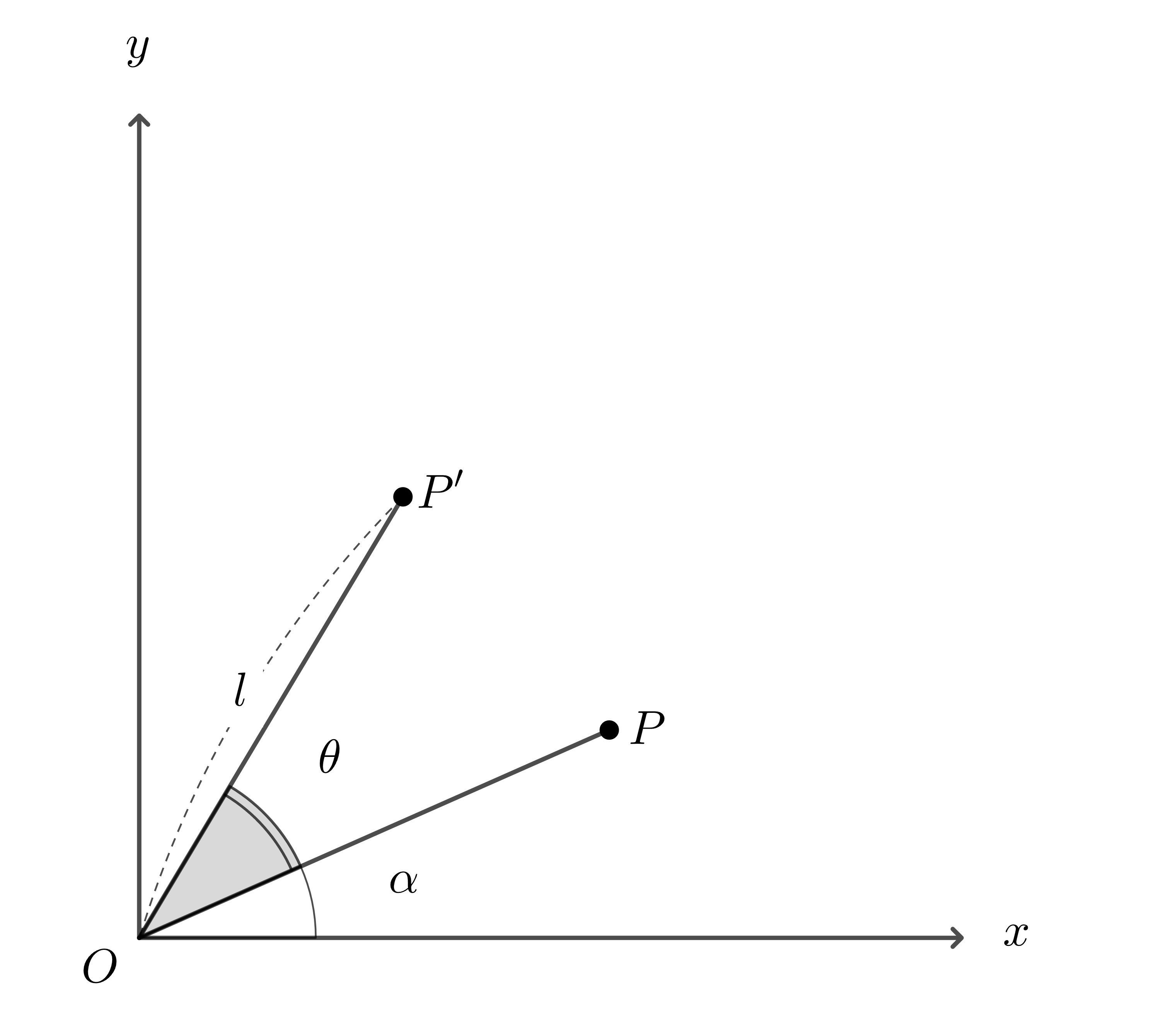
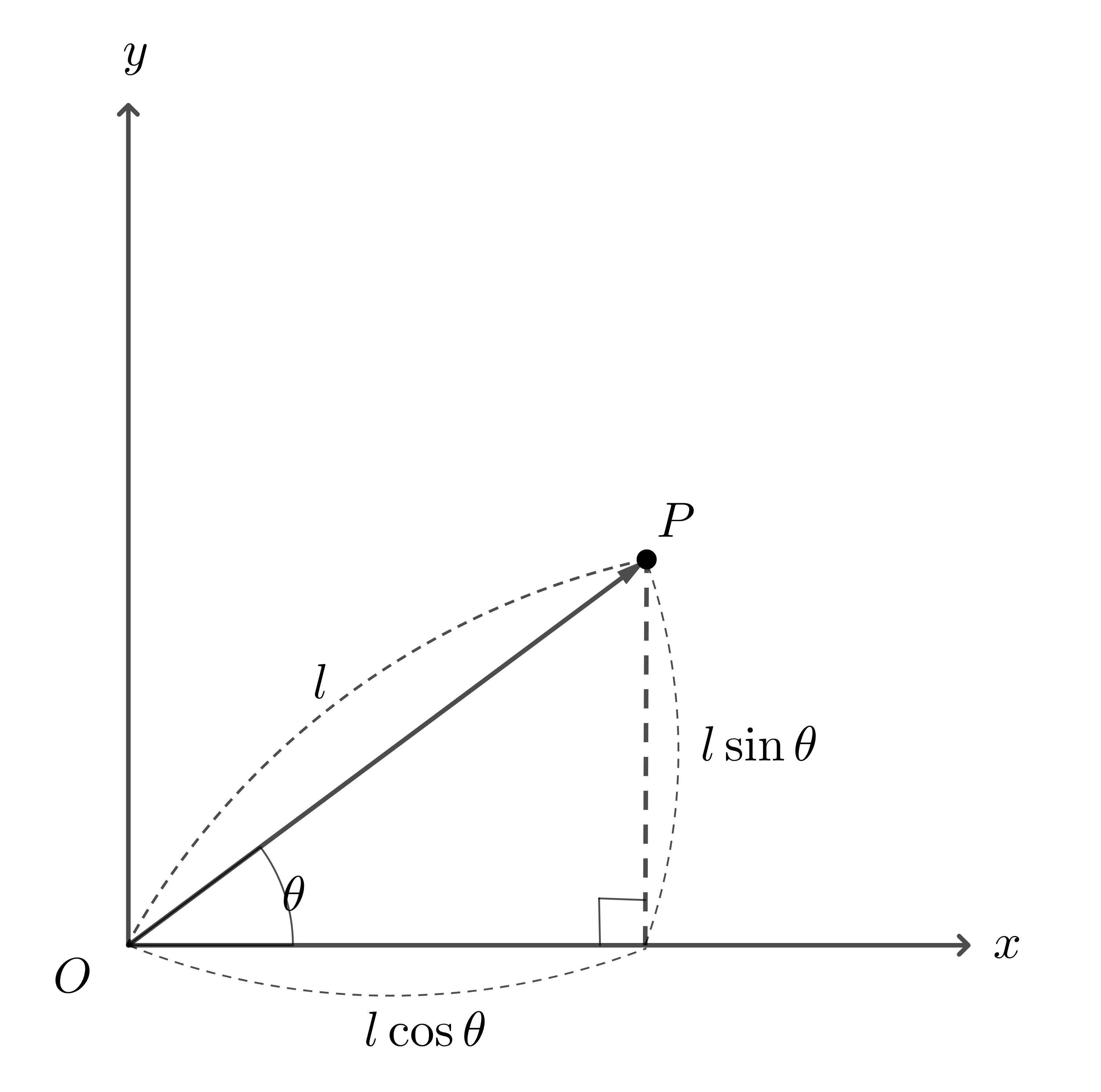
위의 그림1에서 회전되지 않은 벡터 $P$와 각도 $\theta$만큼 회전된 벡터 $P’$이 있을 때, 각각의 좌표는 다음과 같다 (그림2)

\[\begin{equation} P = \begin{bmatrix} l\cos{\alpha} \\ l\sin{\alpha} \end{bmatrix} \end{equation}\] \[\begin{equation} P' = \begin{bmatrix} l\cos{\left(\alpha + \theta\right)} \\ l\sin{\left(\alpha + \theta\right)} \end{bmatrix} \end{equation}\]

이때 삼각함수의 합 공식을 사용하여 $P’$을 분해하면 다음과 같다.

\[\begin{equation} P' = \begin{bmatrix} l\cos{\alpha}\cos{\theta} - l\sin{\alpha}\cos{\theta} \\ l\sin{\alpha}\cos{\theta} + l\cos{\alpha}\sin{\theta} \end{bmatrix} \end{equation}\]

이를 행렬로 나타내면 다음과 같다.

\[\begin{align} \begin{bmatrix}\cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta}\end{bmatrix} \begin{bmatrix} l\cos{\alpha} \\ l\sin{\alpha} \end{bmatrix} &= \begin{bmatrix}l\cos{\alpha}\cos{\theta} - l\sin{\alpha}\cos{\theta} \\ l\sin{\alpha}\cos{\theta} + l\cos{\alpha}\sin{\theta}\end{bmatrix} \\ \begin{bmatrix}\cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta}\end{bmatrix} P &= P' \end{align}\]

이를 정리하면, 길이가 $l$ 이고 각도가 $\theta$ 인 점 $P$를 $P(l, \theta)$로 표기했을 때, 다음과 같다. \(\begin{equation} \begin{bmatrix}\cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta}\end{bmatrix} P(l, \alpha) = P(l,\alpha + \theta) \\ \end{equation}\)

그리고 이때의 행렬 R을 회전 행렬(Rotation Matrix)라 한다. \(\begin{equation} \begin{bmatrix}\cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta}\end{bmatrix} = R(\theta) = R \end{equation}\)

회전 행렬의 재미있는 몇가지 성질들

우리는 2차원 평면 위의 점에 대한 회전 변환 행렬을 구했다. 고등학교 수준의 삼각함수 합성에 대해서만 알면 어렵지 않게 유도할 수 있다. 하지만 유도 과정보다 더 주목할 만한 점은, 회전 행렬의 특이한 형태이다.

일단 $\theta$에 의해서 회전 행렬 $R$의 4개 성분이 전부 정해진다는 것을 볼 수 있다. 이는 즉, 2차원 평면 위의 회전을 표현하는데 필요한 최소한의 scalar 값의 개수가 1개라는 것을 의미한다. 이론상으로 1개의 스칼라값 만으로 자세를 결정짓는 것이 가능하다는 것이다.

물론 미분이나 적분이 가능한지 매끄러운지는 모르겠지만(이는 자세의 표현 방법에 따라 다르다), 2차원 평면의 모든 자세는 1개의 스칼라 값에 의해 표현될 수 있다는 뜻이다.

또한, 2x2의 정방행렬(Square Matrix)이므로 모든 행 또는 열벡터가 서로 선형 독립이라면 이 회전 행렬 $R(\theta)$의 역행렬 $R(\theta)^{-1}$ 역시 존재할 수 있다. 그리고 이 경우, 계산해보면 회전 행렬의 역행렬은 반드시 존재함을 알 수 있다.

역행렬의 형태도 재미있는데, 직접 계산해서 형태를 확인해 보면 다음 성질을 확인할 수 있다.

\[\begin{equation} R(\theta)^{-1} = R(\theta)^T = R(-\theta) \end{equation}\]

당연히 이는 우연이 아니며, 회전 변환 행렬의 각 열벡터와 행벡터의 의미를 알게 된다면 정말 자연스러운 특성이라는 것을 알 수 있다.
이를 유도하고 증명해보는 과정도 꽤 재밌는데, 나중에 따로 포스트 하도록 하겠다.