내부점 방법(Interior Point Method)

장벽을 높여가며 부등식 제약 조건 내부에서 최적해를 찾는 Interior Point Method에 대해 알아보자

참고 1 : Interior point method
참고 2 : 모두를 위한 컨벡스 최적화, barrior methods
참고 3 : CMU-convex optimiazation, barrior methods
참고 4 : Barrier Function

Interior Point Method

내부점 방법(Interior point method)은 barrier method 또는 IPM 이라고도 불린다.
convex optimization 문제에 대해서 linear와 non-linear 모두에 적용 가능하며. 특히 부등식 제약 조건이 있는 최적화 문제를 해결할 수 있다.

등식 제약 조건은 Newton’s method 과 라그랑주 승수법(Lagrange multiplier method)을 사용하여 iterative하게 계산할 수 있었다.

하지만, 부등식 제약 조건은 이보다 더 까다로운 문제이다. KKT Condition 에서 부등식에 관련된 조건을 살펴보면, 부등식의 경계에선은 제약 조건처럼 행동하지만, 내부에서는 제약 조건이 없는 것처럼 행동한다.

이러한 부등식 제약 조건을 해결하기 위해, Interior Point Method는 부등식 제약 조건을 부드럽게 만들어주는 장벽 함수(Barrier Function)을 도입한다. 이 장벽 함수는 부등식 제약 조건을 만족하는 영역으로 제한하며 파라미터에 따라 더 날카롭게 만들 수도 있다.

자세한 내용은 다음과 같다.

내부점 방법(Interior point method)

기존의 최적화 문제가 다음과 같을 때 \(\begin{align} \min_x & \quad f(x) \nonumber \\ \text{s.t. } & \quad h_i(x) \leq 0, i = 1 ... m \nonumber \\ & \quad l_j(x) = 0, j = 1 ... r \end{align}\)

부등식 제약을 log barrier function 으로 대체한다. \(\begin{align} \min_x & \quad f(x) - \frac{1}{t} \sum_{i=1}^{m} \log(-h_i(x)) \nonumber \\ \text{s.t. } & \quad l_j(x) = 0, j = 1 ... r \end{align}\)

feasible set $D$에 대해 초기값 $x_0 \in D$,$t_0$, 상수 배율 $\mu > 1$을 정하고 다음 절차를 따른다

1. $t = t_0$으로 초기화하고, $x = x_0$으로 초기화한다.
2. $x$가 optimal point에 수렴할 때까지 다음을 반복한다.
   2-1. $x$에 대한 KKT condition을 만족하는 $s$를 찾는다.
   2-2. $x$를 $x + \alpha s$로 업데이트한다. 여기서 $\alpha$는 backtracking line search를 사용하여 찾는다.
   2-3. $x$가 feasible set $D$에 가까워질 때까지 $t$를 $\mu t$로 업데이트한다.

여기서 절차 2번의 내용은 newton method를 주로 사용한다. 또한 세부적인 내용은 전략에 따라 조금씩 다른데, 포스트의 마지막에서 소개하겠다.

$t$값이 커질 수록, log barrier function은 경계에서 점점 더 날카로워진다. 처음에는 barrier를 완만하게 세워놓고, newton’s method 등의 방법으로 새로운 내부점으로 step을 밟는다.
다음 step에서는 $t$ 값을 약간 더 키워서 log barrier function을 더 높고 날카롭게 만들어 부등식 제약을 점점 강하게 적용한다. 이러한 과정을 반복하면서 최적해를 찾아가는 것이다.

이제 내부점 방법(Interior point method)에 대해 자세히 알아보자

Barrier Function

등장 배경

다음과 같은 부등식 제약 조건이 있는 컨벡스 최적화 문제가 있다고 하자.

\[\begin{align} \min_x & \quad f(x) \nonumber \\ \text{s.t. } & \quad h_i(x) \leq 0, i = 1 ... m \nonumber \\ & \quad l_j(x) = 0, j = 1 ... r \end{align}\]

부등식 제약이 포함된 문제에서는 현재 어떤 제약 조건이 해를 찾는 데에 제약을 주는지 파악하기 힘들다. 특히, feasible set의 경계(부등식 제약 조건이 0인 지점)에서는 등식 제약 조건 외에, 부등식 제약 조건의 일부도 등식 제약 조건처럼 행동해야 한다.

위 문제의 라그랑지안은 다음과 같이 표현할 수 있다.

\[\begin{align} \mathcal{L}(x, \lambda, \nu) = f(x) + \sum_{i=1}^{m} \lambda_i h_i(x) + \sum_{j=1}^{r} \nu_j l_j(x) \nonumber \\ (\lambda_i > 0) \end{align}\]

KKT 조건의 complementary slackness 조건은 다음과 같았는데 :

\[\begin{align} \lambda_i h_i(x) = 0, i = 1 ... m \end{align}\]

이는 부등식 제약 조건의 내부점에서는 $\lambda_i = 0$이 되어서 아무런 제약을 주지 않고, 경계에서는 $h_i(x) = 0$이 되어서 등식 제약 조건처럼 행동하게 한다.

부등식의 경계 바깥에서는 KKT 조건이 먹히지 않는다. 이때 특정 부등식 제약 조건, $g_i(x) > 0, \lambda_i > 0$이 되므로 라그랑지안 함수 중 $\lambda_i h_i(x)$부분에 의해 $\max_{\lambda, \nu} \mathcal{L} = \infty$로 발산하게 된다.

위와 같은 특성을 최대한 유지하면서 목적함수에 합칠 수 있는 방법이 있는데, 바로 지시함수(Indicator function)를 사용하는 것이다.

Indicator function

지시함수의 정의는 다음과 같다 :

\[\begin{align} I(x) = \begin{cases} 0 & \text{if } x \leq 0 \\ \infty & \text{if } x > 0 \end{cases} \end{align}\]

이를 사용해서 부등식 제약 조건을 다음과 같이 목적 함수에 합치면 다시 제약 조건 최적화 문제로 변환할 수 있다.

\[\begin{align} \min_x & \quad f(x) + \sum_{i=1}^{m} I(h_i(x)) \nonumber \\ \text{s.t. } & \quad l_j(x) = 0, j = 1 ... r \end{align}\]

이는 $h_i(x)$들 중 단 하나라도 0보다 커지면, 즉시 목적함수가 $\infty$으로 발산하므로, 부등식 제약 조건을 만족하는 영역으로 solution을 제한하는 효과가 있다.

하지만 여전히 boundary 관련해서 문제가 많은데, 특히 지시함수의 미분이 불가능 하다는 점이 큰 문제다. differentiable 하지 않기 때문에 gradient descent, newton method 등의 방법을 적용할 수 없다.

이 문제를 해결하고자 고안된 방법이 barrier function과 barrier method 이다.

Logarithmic Barrier Function

Barrier function은 기존의 Indicator function을 부드럽게 만들어 boundary 근처에서도 미분이 가능하도록 만든 함수이다. 여기에 한술 더 떠서 어떤 파라미터 $t$ 값을 조정함으로써 장벽의 기울기와 날카로운 정도도 조절할 수 있으면 더욱 좋다.

위 조건에 전부 부합하면서 미분도 쉬운 함수 중 하나가 바로 log barrier function이며, 다음과 같다 :

\[\begin{align} B(x) = - \log(-h_i(x)) \end{align}\]

이 함수는 $h_i(x) \leq 0$인 영역에서는 0에 가까운 값을 가지고, $h_i(x) = 0$인 영역에서는 $\infty$으로 발산한다. $h_i(x) > 0$은 아예 정의역이 아니여서 불가능하다. 이는 마치 장벽(Barrier)와 같지만 미분이 가능하다.

거기다가 앞에 계수를 곱하면, 장벽의 기울기도 조절할 수 있다.
$-(1/t)\log(-h(x))$에서 $t=0.5, 1, 2$일 때를 각각 그리면 다음과 같다 :

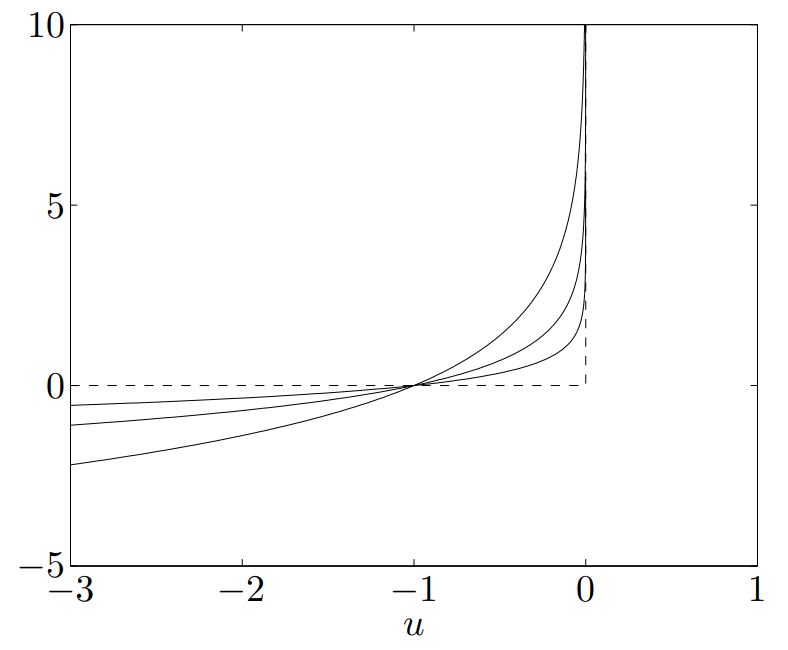log barrier function의 그래프와 Indicator Function

$t$가 커질수록 장벽이 날카로워짐을 볼 수 있다.

이를 기존의 목적함수에 합치면, 다음과 같은 목적함수를 얻을 수 있다.

\[\begin{align} \phi(x) &= -\sum_{i=1}^m \log(-h_i(x)), \text{barrier term} \\ \min_x & \quad f(x) +\frac{1}{t} \phi(x)\nonumber \\ & \Rightarrow tf(x) + \phi(x) \nonumber \\ \text{s.t. } & \quad l_j(x) = 0, j = 1 ... r \end{align}\]

이렇게 기존의 부등식 제약 조건 최적화 문제를, barrier function을 사용해서 변환한 것을 barrier problem 이라 한다. barrier problem을 newton method를 사용해서 풀어나가는 방법을 barrier method라 하며, 이를 이용한 최적화 방법을 Interior Point Method라고 한다.

$t$가 작을 땐, feasible set 안에서도 본래의 목적함수 $f(x)$보다, barrier term의 영향력이 더 크다. 하지만 점차 $t$가 커져감에 따라 본래의 목적함수 $f(x)$의 영향력이 커지며 동시에 barrier term의 영향력은 줄어든다.

따라서 처음에는 $t$를 작게 잡아서 Newton method를 사용해 feasible set 안에서도 최적해를 찾아가다가, 점차 $t$를 키워가며 feasible set의 경계에서 최적해를 찾아가는 것이다.

그 모습이 마치 내부의 점(Interior point)를 잡아서 움직이는 것과 같기 때문에 Interior Point Method라고 불린다.

Calculus of barrier function

logarithmic barrier function의 그라디언트와 헤시안은 다음과 같다 :

\[\begin{align} \nabla \phi(x) &= - \sum_{i=1}^m \frac{\nabla h_i(x)}{h_i(x)} \nonumber \\ H_\phi(x) &= \sum_{i=1}^m \frac{1}{h_i(x)^2} \nabla h_i(x) \nabla h_i(x)^T - \frac{1}{h_i(x)} H_{h_i}(x) \end{align}\]

Central Path

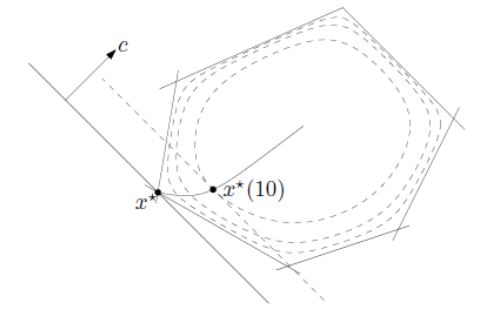
Interior point method가 시작부터 수렴까지 거치는 경로를 Central path라고 한다.

Centerion step $x^* (t)$ f를 수식으로 표현하면 다음과 같다 :

\[\begin{align} \min_x & \quad tf(x) + \phi(x) \nonumber \\ \text{s.t. } & \quad l_j(x) = 0, j = 1 ... r \\ \\ x^* (t) & \text{: solution of problem at } t, t >0 \\ \end{align}\]

이때 적절한 조건이 주어지면 centering step은 $\mathbb{R}^n$ 에서 smooth path가 되며, $t \rightarrow \infty$ 일 때 $x^* (t) \rightarrow x^*$ 로 수렴한다.

Interion point method가 각각의 $t$에 대해 centering step을 수행하면서 feasible set의 경계를 따라 이동하며 최적해를 찾아가는 것이다.

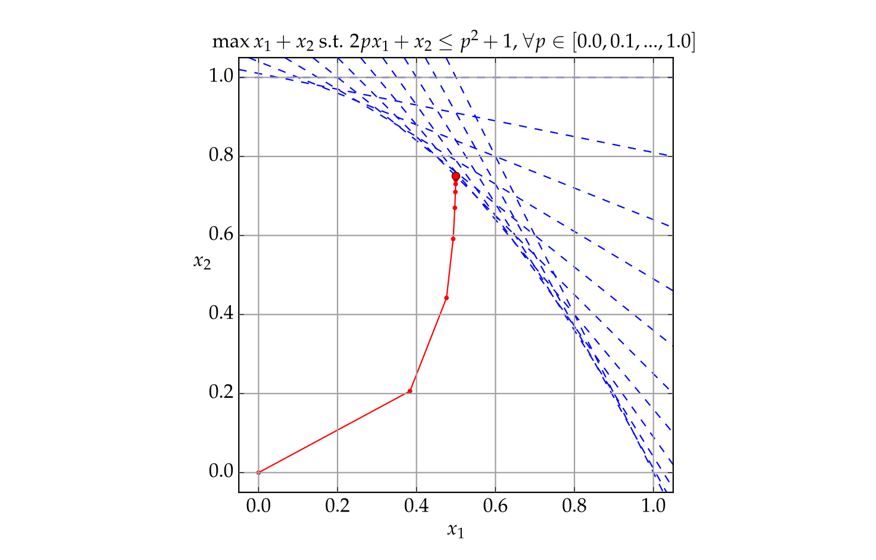
예시로 LP 문제에 대한 centering step을 그려보면 다음과 같다

선형 문제의 Central Path의 모습

Interpretation & Properties

Perturbed KKT Condition

barrier problem 사이의 KKT 조건을 따져보고, 무엇이 바뀌었는지 비교해보자.

log barrier function은 KKT 조건식 중, complementary slackness 조건을 다음과 같이 바꾼다.

\[\begin{align} \lambda_i h_i(x) = - \frac{1}{t}, i = 1 ... m \end{align}\]

이 식을 살펴보면, $t$가 커질수록 0에 가까워져서 원래의 complementary slackness 조건에 가까워진다.

이제 바뀐 조건으로 KKT 조건 중, stationary condition을 살펴보자.

\[\begin{align} \nabla f(x) + \sum_{i=1}^m \lambda_i \nabla h_i(x) = 0 \nonumber \\ \Rightarrow \nabla f(x) - \sum_{i=1}^m \frac{1}{t} \frac{\nabla h_i(x)}{h_i(x)} = 0 \nonumber \\ \Rightarrow \nabla \left( f(x) - \frac{1}{t} \sum_{i=1}^m \log{(-h_i(x))} \right)=0 \nonumber \\ \Rightarrow \nabla \left( tf(x) + \phi(x) \right) = 0 \end{align}\]

이렇게 바뀐 KKT 조건을 perturbed KKT condition이라고 하며, log barrier function의 형태가 나타남을 확인할 수 있다.

Suboptimality Gap

여기서, $x^* $가 최적해라고 할 때, centering step $x^* (t)$를 생각해 보자.

라그랑지안 $\mathcal{L}(x, \lambda, \nu)$에 대해서, $t$에서의 각각의 $\lambda, \nu$를 $\lambda^* (t), \nu^* (t)$라 하면. 다음이 성립한다 :

\[\begin{align} x^* (t) &= \min_x \mathcal{L} (x, \lambda^* (t), \nu^* (t)) \nonumber \\ &:= g(\lambda^* (t), \nu^* (t)) \\ \nonumber \\ g(\lambda^* (t), \nu^* (t)) &=f(x^* (t)) + \sum_{i=1}^m \lambda_i^* (t) h_i(x^* (t)) + \sum_{j=1}^r \nu_j^* l_j(x^* (t)) \\ &= f(x^* (t)) - \frac{m}{t}, \quad \text{As }\lambda_i g_i(x) = -\frac{1}{t}, l_j(x^* (t))=0 \nonumber \\ &\leq f(x^* ) \end{align}\]

따라서 둘 사이의 gap에 대한 부등식은 다음과 같다.

\[\begin{align} & f(x^* (t)) - f(x^*) \leq \frac{m}{t} \\ m &\text{ : number of inequality constraints} \nonumber \end{align}\]

이 식은 convergence analysis에 사용되며, 추후에 primal-dual method 에서도 사용된다.

Interior Point Method의 종류

다음 부등식 제약 컨벡스 최적화 문제가 주어졌다고 하자 :

\[\begin{align} \min_x & \quad f(x) \nonumber \\ \text{s.t. } & \quad h_i(x) = 0, i = 1 ... m \nonumber \\ & \quad l_j(x) \leq 0, j = 1 ... r \end{align}\]

Barrier function을 사용하여 barrier problem으로 문제를 변환한다

\[\begin{align} \min_x & \quad tf(x) + \phi(x) \nonumber \\ \text{s.t. } & \quad l_j(x) = 0, j = 1 ... r \end{align}\]

여기까진 같지만, 이후 세부적인 내용은 약간씩 다르다

Path-Following Method

이때 특정 duality gap을 만족하기 위해서, 임의의 작은 양수 $\epsilon >0$을 잡는다. 그리고 $m/t \leq \epsilon$이 되게 하는 $t>0$값 까지 $t$를 점차 증가시키면서 centering step을 수행한다.

알고리즘을 설명하면 다음과 같다 :

1. 원하는 duality gap을 정한다. $m/t \leq \epsilon$, $\epsilon >0$인 작은 양수를 정한다.
2. $t=t_0$으로 초기화한다.
3. $t_0$에서의 barrier problem을 한번 풀어서 $x_0 = x^* (t_0)$를 구한다.
4. $m/t < \epsilon$ 인지 확인한다. 만족하면 그때의 $x$를 최적해로 반환한다.
   4-1. $t_{k+1} = \mu t_k$로 업데이트 한다. $\mu > 1$인 상수로 설정한다.
   4-2. $t_{k+1}$ 에서의 barrier problem을 Newton method로 푼다. 이때 초기 위치를 $x_k$를 사용한다. (warm start)
   4-3. barrier problem을 푼 해를 $x_{k+1} = x^* (t_{k+1})$ 로 놓고 4번으로 돌아간다.

• 일반적인 $t$의 업데이트 방법은 $t_{k+1} = \mu t_k$, $\mu > 1$로 상수곱을 통해 업데이트 하는 것이다.

• warm start는 이전 newton step의 결과물을 다음 newton step의 시작점으로 잡는다. 이 시작점들은 newton method가 대부분 바로 quadratic convergence를 하게 만듦으로써 전체적인 수렴속도를 높인다.

• Centering step은 3,4 단계에서 barrier problem을 푼 결과값들을 말한다. outer iteration 이라고도 한다. inner iteration은 각 barrier problem을 풀 때의 newton method에서 발생한 iteration이다.

고려할 점은 다음과 같다

1. $\mu$ 의 선택
   너무 작다면 outer iteration이 많아지고, 너무 크다면 inner iteration이 많아진다. 적절한 값을 찾아야 한다.

2. 초기 $t_0$의 선택
   너무 작으면 outer iteration이 많아지고, 너무 크면 처음부터 원래 문제에 지나치게 가까워 barrier problem을 푸는데 어려움을 겪는다. 따라서 첫번째 centering step에서 $x_0$을 찾는데 시간이 오래 걸린다.

Potential Reduction Method

위의 path-following method에서는 $t$를 점차 증가시키면서 centering step을 밟았지만, Potential Reduction method는 $t$가 변화하지 않는다.

대신 $m/t \leq \epsilon$을 통해 얻은 $t$값을 집어넣은 barrier problem을 단 한번만 품으로써 최적해를 찾는 방식이다.

path centering step을 아예 하지 않으니, path-following 방식보다 좋을 것 같지만, 현실은 오히려 path-following 방식이 많이 사용된다.

왜냐하면 Potential Reduction method는 초기 $t$값을 잘 선택해야 하며, 이는 문제에 따라 다르기 때문이다. 부적절한 $t$값을 고르면 수렴이 매우 오래걸리거나 안 되는 경우가 생긴다.

하지만 path-following 방식은 $\mu$값을 잘 선택하면 대부분 잘 수렴하고 안정적인 내부 영역에서 centering step을 밟으며 $t$값을 점진적으로 줄여나가기 때문에 안정적이라는 장점이 있다.

Primal-Dual Method

Primal-Dual method는 barrier problem을 푸는 대신, primal-dual problem을 푼다.

primal과 dual 양쪽을 동시에 고려함으로써 반드시 $x^* (t) \in D$일 필요가 없으며, 기존 방법에 비해 수렴 속도도 빠르다. 특히 비선형성이 강하고, 제약 조건이 복잡한 문제에서 path-following method보다 더 좋은 성능을 보인다.

다만 구현 난이도가 높은 편이며, primal-dual problem을 푸는 것이니 만큼, 변수가 더 늘어난다.

다음 포스트에서 구체적으로 알아보자.