슬라이딩 퍼즐의 불변량
슬라이딩 퍼즐이 항상 유지하는 어떠한 성질은 무엇인가
참고 1 : https://en.wikipedia.org/wiki/Parity_of_a_permutation
참고 2 : https://dec41.user.srcf.net/notes/IA_M/groups.pdf
참고 3 : https://en.wikipedia.org/wiki/15_puzzle#Solvability
참고 4 : https://jweilhammer.github.io/sliding-puzzle-solver/
슬라이딩 퍼즐과 순열의 부호
지금까지 군의 정의부터 시작해서 부분군, 대칭군, 순열의 부호까지 쌓은 빌드업을 활용할 시점이 왔다.
먼저 우리가 상대할 슬라이딩 퍼즐을 임의의 크기가 아니라, 4x4 크기의 퍼즐로 한정짓자. (15 퍼즐) 이는 4x4 퍼즐이 가장 유명하고, 딱 직관과 추상 수학의 경계에 걸쳐있는 복잡도를 가지고 있다고 생각하기 때문이다.
조각을 순열로 보기
먼저 슬라이딩 퍼즐의 조각을 순열로 보는 방법을 다시 상기하자.
슬라이딩 퍼즐의 조각은 1~15까지의 숫자와 하나의 빈칸으로 이루어져 있다.
빈칸도 하나의 조각으로 생각한다면, 이는 총 16개의 조각을 뒤섞는 문제로 볼 수 있다. 즉, 이는 16개의 원소를 가지는 집합 {1, 2, .. , 15, 16(빈칸)}을 뒤섞는 문제로 볼 수 있다.
직전의 포스팅에서 다룬 바와 같이, 16개의 원소를 뒤섞는 모든 방법을 모은 집합이 바로 대칭군, $S_{16}$이다.
하지만 슬라이딩 퍼즐이 할 수 있는 조각의 이동은 조건이 있다.
인접한 조각과의 1대1 교환(transposition)만 가능하다는 것이며, 그 마저도 양 옆 외에 슬라이딩 격자의 모양에 따라 위아래로도 교환이 가능하다.
혹시 이러한 제약 자체가 어떠한 성질을 유지하게 만들지는 않을까?
빈칸을 움직일 때 벌어지는 일
슬라이딩 퍼즐을 움직이면서 현재 조각의 순열이 어떻게 변하는 지를 보자.
빈칸을 $i$번 째 움직여서 나타내는 순열을 $\sigma_i, \quad i$ = 0, 1, 2, … 로 정의하며 추적한다.
모든 조각이 제자리에 있는 상태부터 시작하자.
현재 $\sigma_0 = e$이 된다. (항등원)
이 상태에서 빈칸을 옆으로 움직여 보면,
이는 $e$에 (16 15)라는 transposition을 수행한 것과 같다.
즉, $(16\ 15) \cdot \sigma_0 = (16\ 15) = \sigma_1$이다.
이제 여기서 위로도 움직여 보자
이는 (15 11)라는 transposition을 수행한 것과 같다.
즉, $(15\ 11) \cdot \sigma_1 = (11 \ 15 \ 16) = \sigma_2$이다.
규칙이 보이는가?
빈칸을 움직일 때마다, 현재 순열에 어떤 transposition을 왼쪽에 곱하는 것과 같다.
이전 포스팅에서 순열의 부호 함수에 대해서, 다음 성질이 있음을 보였다.
현재 상태의 순열이 $\sigma_i$이고, 빈칸을 움직여서 $\sigma_{i+1}$이 되었다고 한다면, 빈칸과 다른 인접조각과의 교환을 transposition, $\tau_i$라고 하자.
이때 transposition의 부호이므로 $\text{sgn}(\tau_i) = -1$이다.
그러면 다음과 같은 식이 성립한다 \(\begin{align} \sigma_{i+1} &= \tau_i \cdot \sigma_i \\ \text{sgn}(\sigma_{i+1}) &= \text{sgn}(\tau_i) \cdot \text{sgn}(\sigma_i) \\ \therefore \text{sgn}(\sigma_{i+1}) &= - \text{sgn}(\sigma_i) \end{align}\)
즉, 빈칸을 움직일 때마다 현재 순열의 부호가 바뀌게 된다. 더욱이 초기 상태에서 $\sigma_0 = e$이므로, $\text{sgn}(\sigma_0) = 1$로 시작한다는 것도 알 수 있으므로 다음이 성립한다 :
\[\text{sgn}(\sigma_i) = (-1)^i\]하지만 이건 아직 슬라이딩 퍼즐이 ‘유지’하는 성질은 아니다.
어쨌든 빈칸을 움직일 때마다 부호가 바뀌기 때문이다.
이걸 변하지 않는 성질로 만들려면, 빈칸이 움직인 횟수가 짝수인지, 홀수인지도 같이 고려해야 한다.
현재 슬라이딩 퍼즐의 상태만 보고 이 퍼즐이 빈칸을 짝수번 움직였는지, 홀수번 움직였는지를 알 수 있을까?
빈칸이 움직인 횟수를 고려하기
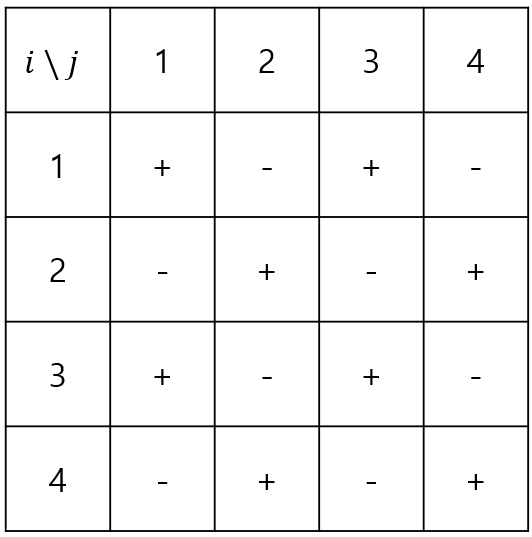
임의로 빈칸이 (1,1)부터 시작한다고 가정하고, 초기 빈칸의 상태를 +로 표시하고, 빈칸을 움직일 때 마다 +, -를 번갈아 붙여보자.
직감적으로 다음과 같이 그려질 거라는 걸 쉽게 예상할 수 있다.
이는 마치 체스판의 흑백 패턴과 비슷하다.
좀 더 수식화 하면, 각 칸의 좌표 $(a, b)$에서, $a + b$가 짝수이면 +, 홀수이면 -가 붙으므로, 다음과 같이 표현할 수 있다 :
\[(-1)^{a+b}\]여기까진 굳이 증명하지 않아도 직관적으로 느껴지지만, 이게 정말로 슬라이딩 퍼즐에서 빈칸이 (1,1)로부터 움직인 횟수의 홀짝성과 일치하는지 훨씬 멋있게 증명해보자.
증명
먼저 홀짝성/패리티(parity)를 정의하겠다 :
홀짝성/패리티 함수
\[\pi(n) = n \mod 2\]
즉 $n$이 짝수이면 $\pi(n) = 0$, 홀수이면 $\pi(n) = 1$이다.
어떤 두 정수 $n, m$에 대해서,
만약 둘 다 짝수이거나 둘 다 홀수라면, 그 합이 짝수가 된다.
만약 둘 중 하나가 홀수, 다른 하나가 짝수라면, 그 합은 홀수가 된다.
즉, 다음이 성립한다 :
\[\pi(n + m) \equiv \pi(n) + \pi(m) \mod 2\]맨 처음 빈칸의 위치를 (1,1)라고 했을 때, 슬라이딩 퍼즐이 가능한 모든 움직임은, 상하좌우의 4가지 움직임 뿐이다.
만약 초기 위치 (1,1)에서 상하좌우의 움직임을 각각 $m_0, m_1, m_2, m_3$번 했다고 하면, 최종 위치 (a,b)는 다음과 같이 표현할 수 있다 :
이제 첫번째 식의 양변에 parity를 취하면 다음을 얻는다 :
\[\begin{align} \pi(a) &\equiv \pi(1 + m_1 - m_0) \\ &\equiv \pi(1) + \pi(m_1 - m_0) \\ &\equiv 1 + \pi(m_1 - m_0) \end{align}\]다음으로 $m_0 + m_1$과의 홀짝성을 비교해보자 :
\[\begin{align} \pi(m_1 - m_0) &\equiv \pi((m_0 + m_1) - 2m_0) \\ &\equiv \pi(m_0 + m_1) + \pi(-2m_0) \\ &\equiv \pi(m_0 + m_1) + 0 \\ \\ \therefore \pi(a) &\equiv \pi(m_0 + m_1) + 1 \mod 2 \\ \end{align}\]즉, $a$의 홀짝성은 $m_0 + m_1$의 홀짝성과 반대임을 알 수 있다.
똑같은 논리를 두번째 식에도 마저 적용해서 :
\[\begin{align} \pi(b) &\equiv \pi(1 + m_3 - m_2) \\ &\equiv 1 + \pi(m_3 - m_2) \\ &\equiv 1 + \pi(m_2 + m_3) \end{align}\]을 얻을 수 있다.
이제 우리가 관심있는 $\pi(m_0 + m_1 + m_2 + m_3)$를 구해보자 :
\[\begin{align} \pi(m_0 + m_1 + m_2 + m_3) &\equiv \pi(m_0 + m_1) + \pi(m_2 + m_3) \\ &\equiv \pi(a) + 1 + \pi(b) + 1 \\ &\equiv \pi(a) + \pi(b) \mod 2 \\ \end{align}\]즉, 빈칸이 움직인 횟수의 홀짝성은, 최종 위치 $(a,b)$의 좌표 합의 홀짝성과 일치함을 훨씬 더 형식적으로 증명했다.
물론, 두 수를 더해서 짝/홀이 될 경우의 수를 쫙 펼쳐서 일일이 대조해도 되지만,
패리티 함수 \(\pi(n) = n \mod 2\)를 정의하고 그 성질을 이용해서 증명하는 게 더 깔끔하고 멋있다.
준비는 끝났다. 슬라이딩 퍼즐의 불변량(invariant)을 정의하고 증명해보자.
슬라이딩 퍼즐의 불변량(invariant)
이제 슬라이딩 퍼즐이 유지하는 성질을 정의할 수 있다.
\[I(\sigma) = \text{sgn}(\sigma) \cdot (-1)^{a+b}\]슬라이딩 퍼즐의 불변량
\[I(\sigma, a, b) = \text{sgn}(\sigma) \cdot (-1)^{a+b}\]$\sigma$는 세로가 $n$칸, 가로가 $m$칸인 슬라이딩 퍼즐에서, 슬라이딩 퍼즐을 현재 상태로 섞는 순열 $\sigma \in S_{nm}$로 정의된다.
현재 빈칸의 좌표 $(a, b)$는 슬라이딩 퍼즐의 좌측 상단을 (1,1)로 하고, 우측 하단을 (n,m)으로 하는 2D 좌표계에서 나타낸다.
여기서 $(a,b)$는 그림 4에서 보여준 식으로 빈칸의 좌표를 나타낸 것이다.
이제 이 $I(\sigma)$가 슬라이딩 퍼즐이 유지하는 성질, 즉 불변량(invariant)임을 보이자.
불변량 증명
슬라이딩 퍼즐의 상태를 나타내는 순열이 $\sigma_i$에서 $\sigma_{i+1}$로 바뀌었다고 하자.
즉, 빈칸이 움직여서 상태가 바뀌었고, 그 때 빈칸의 좌표가 $(a,b)$에서 $(a’, b’)$로 바뀌었다고 하자.
이 때 빈칸을 움직이는 움직임은 transposition 임을 앞에서 보였고, 그걸 $\tau_i$라고 하자.
이제 다음이 성립한다 :
\[\begin{align} \sigma_{i+1} &= \tau_i \cdot \sigma_i \\ \text{sgn}(\sigma_{i+1}) &= \text{sgn}(\tau_i) \cdot \text{sgn}(\sigma_i) \\ \therefore \text{sgn}(\sigma_{i+1}) &= - \text{sgn}(\sigma_i) \end{align}\]다음으로, 빈칸의 좌표를 움직일 수 있는 4가지 방향에 대해서, $(a,b)$에서 $(a’, b’)$로 바뀌는 경우를 모두 고려해보자.
각각 위아래 방향으로 +1, -1, 좌우 방향으로 +1, -1 움직이는 경우이다.
이 때 빈칸의 좌표의 합은, $a+b \rightarrow a+b \pm 1$ 로만 변할 수 있다.
앞서 패리티에 대해 증명한 성질을 사용하면 :
\[\begin{align} \pi(a' + b') &\equiv \pi(a + b) \pm 1 \mod 2 \\ &\equiv \pi(a+b) + 1 \mod 2 \end{align}\]즉, $(-1)^{a’ + b’} = - (-1)^{a + b}$이다.
이제 위의 두 결과를 종합하여 다음을 얻는다 :
\[\begin{align} I(\sigma_{i+1}, a', b') &= \text{sgn}(\sigma_{i+1}) \cdot (-1)^{a' + b'} \\ &= - \text{sgn}(\sigma_i) \cdot - (-1)^{a + b} \cdot \\ &= \text{sgn}(\sigma_i) \cdot (-1)^{a + b} \\ &= I(\sigma_i, a, b) \end{align}\]이렇게 $I(\sigma)$는 슬라이딩 퍼즐을 아무리 움직여도 변하지 않는 성질, 즉 불변량(invariant)임을 보였다.
즉, 다음이 보장된다 :
$I_0 := I(e, a_0, b_0), \quad (a_0, b_0) \text{는 초기 빈칸의 좌표} $ $I_i := I(\sigma_i, a_i, b_i), \quad (a_i, b_i) \text{는 i번째 움직임 후의 빈칸의 좌표} $
$I_0 \neq I_i \text{ for any } i \geq 1 \implies ( \sigma, a_i, b_i ) \text{ is not solvable by sliding puzzle}$
이제 이 불변량을 가지고 슬라이딩 퍼즐이 해결 가능한 상태인지 아닌지를 보이면 된다.
슬라이딩 퍼즐의 정답 상태는 모든 조각이 제자리에 있으므로, 초기 불변량, $I_0$를 구한 다음, 현재 상태의 불변량 $I_i$와 비교하면 된다.
두 불변량이 같으면 슬라이딩 퍼즐이 해결 가능한 상태이고, 다르면 불가능한 상태이다.
근데 과연 그럴까? 우린 뭔가 놓치고 있는 게 있다
반쪽짜리 결론으로 마치며
$I_0 \neq I_i$ (단, $i \geq 1$)이면, 슬라이딩 퍼즐이 해결 불가능한 상태라는 건 보장된다.
아무리 조각을 움직여도 불변량이 바뀌는 일은 없으니까.
하지만 $I_0 = I_i$이면 항상 풀 수 있는지(충분조건)은 아직 증명하지 않았다.
즉, 아래 명제에 대한 증명이 아직 남아 있다 :
\[I_0 = I_i, \quad i \geq 1 \implies ( \sigma_i, a_i, b_i ) \text{ is solvable by sliding puzzle ?}\]
한 방향 $p \implies q$가 참이라고 해서, $q \implies p$도 성립하는 건 아니니까.
결국 초기 불변량과 같은 불변량을 가진 상태가 항상 ‘도달 가능한지’ 에 대한 문제가 남아있다.
거기까지 증명해야, 불변량 보존과 해결 가능 여부(solvability)가 완전한 동치관계임을 보일 수 있다.
도달 가능성(reachability)을 보이기 위해서는, 허용된 빈칸 움직임 만으로 같은 불변량을 가지는 모든 상태를 생성할 수 있음을 보여야 한다.
이를 위해서는 conjugation, 대칭군의 conjugacy class, 3-cycle 분해 등 몇 가지 도구가 더 필요하다. 즉, 아직 대칭군에서 볼 것이 남아 있다.
다음 포스트에서 이 개념들을 소개한 뒤, 결국 슬라이딩 퍼즐의 불변량이 해결 가능 여부를 완전히 결정한다는 사실을 증명하겠다.