라그랑주 승수법(Lagrange multiplier method)과 극값 판정

제약이 있는 최적화 문제를 제약이 없는 최적화 문제로 바꾸는 라그랑주 승수(Lagrange multiplier)와 라그랑지안(Lagrangian)에 대해 알아보자

참고 1 : Lagrange multiplier
참고 2 : Bordered Hessian Matrix
참고 3 : 모두를 위한 컨벡스 최적화 - Convex Sets
참고 4 : 모두를 위한 컨벡스 최적화 - Convex Functions
참고 5 : Analytic proof of lagrange, MIT

라그랑주 승수법

정의

라그랑주 승수법은 제약이 있는 최소 & 최대 최적화 문제를 제약이 없는 최적화 문제로 바꾸는 방법이다.

최적화 문제의 제약(constraint)는 여러가지 분류가 있지만, 그 중 하나는 등식 제약(Equality Constraint)과 부등식 제약(Inequality Constraint)이 있다.

부등식 제약 문제도 라그랑주 승수법을 사용해서 바꿀 수 있지만, KKT Condition(카루시-쿤-타커(Karush-Kuhn-Tucker) 조건)에 대해 알아야 이해할 수 있기 때문에, 지금은 다루지 않겠다.

등식 제약이 있는 최소화 문제는 다음과 같이 정의된다 :

Equality constrained optimization problem \(\begin{align} \text{minimize} \quad & f(x) \\ \text{subject to} \quad & g(x)_i = 0, \quad i = 1, 2, \cdots, m \end{align}\)

제약이 없는 상태에서의 최소화 문제는 $f(x)$의 극소값을 찾는 문제였다. 하지만 제약이 있는 최소화 문제는 $f(x)$의 극소값을 찾으면서, $g(x)_i = 0$을 만족하는 $x$를 찾아야 하기에 기존의 방법을 사용할 수 없다.

하지만 라그랑주 승수법을 사용하면, 제약이 있는 최소화 문제를 제약이 없는 최소화 문제로 바꿀 수 있다.

라그랑주 승수법은 제약이 있는 최소화 문제의 최적해(optimal solution) $x^*$가 feasible region의 경계선상에 존재하는게 아니라면, 각각의 그라디언트 벡터들이 다음의 관계를 만족해야 함을 이용한 것이다 :

라그랑주 승수법(Lagrange multiplier method)
\(\begin{align}\nabla f(x^*) &+ \sum_{i=1}^{m} \lambda_i \nabla g_i(x^*)=0, \quad \lambda_i \in \mathbb{R}\\ x^* & \text{: optimal solution inside feasible region} \nonumber\end{align}\)

위의 식에서 $\lambda_i$는 라그랑주 승수(Lagrange multiplier)라고 불리며, 각 제약 조건에 대한 라그랑주 승수를 의미한다.

이 관계를 사용해서 원래의 목적 함수의 형태를 변형해서 제약이 없는 최적화 문제로 만들 수 있으며, 새롭게 만들어지는 이때의 목적 함수를 라그랑지안(Lagrangian) 이라 한다 :

라그랑지안(Lagrangian, $\mathcal{L}$) \(\begin{align} \mathcal{L}(x, \lambda) &= f(x) + \sum_{i=1}^{m} \lambda_i g_i(x) \\ \nonumber \\ \frac{\partial \mathcal{L}}{\partial x} &= \frac{\partial f}{\partial x} + \sum_{i=1}^{m} \lambda_i \frac{\partial g_i}{\partial x} = 0 \nonumber \\ &\Rightarrow \nabla f(x^*) + \sum_{i=1}^{m} \lambda_i \nabla g_i(x^*)=0 \\ \frac{\partial \mathcal{L}}{\partial \lambda_i} &= g_i(x) = 0 \nonumber \\ &\Rightarrow g_i(x^*) = 0 \end{align}\)

라그랑지안의 그라디언트를 0으로 놓고 풀면 위의 라그랑주 승수법과 같은 결과를 얻을 수 있다. 거기에 제약 조건 등식도 자동으로 만족하게 된다. 대신 기존의 변수가 $n$개 였다면, 라그랑주 승수법을 사용한 후에는 변수가 $n+m$개가 된다.

주의할 점은, 라그랑주 승수법으로 구해진 해는 어디까지나 최적해의 후보일 뿐이다. 어디까지나 극점(stationary point)만을 찾아주기 때문에 이게 최소값인지 최대값인지 확인하기 위해서는 추가적인 절차가 필요하다.

크게 두가지의 방법이 있는데, 다음과 같다.

1. Bordered Hessian Matrix를 사용한 극점 판별법
2. 문제 자체가 Convex Problem인지 판별하는 방법

Bordered Hessian Matrix를 사용하여 판별

참고 2 : Bordered Hessian

Bordered Hessian matrix는 라그랑지안의 헤시안 행렬로써, 목적 함수와 제약 조건을 합친 것이다. 이때, 위에서 찾은 optimal solution의 후보, $x^*$를 집어넣어서 Bordered Hessian 행렬의 행렬식을 구하면, 최소값인지 최대값인지 확인할 수 있다.
이때 해당 행렬식의 값이 음수면 minimum, 양수면 maximum이 된다.

bordered hessian 행렬 자체가 positive semidefinite인지 아닌지를 판별하는 것은 의미가 없다. 라그랑지안의 stationary point는 언제나 라그랑지안 함수의 말안장점(saddle point)에 위치하기 때문에, indefinite한 행렬이 나올 수 밖에 없다.

Bordered Hessian의 정의는 다음과 같다 :

Bordered Hessian Matrix
\(\begin{align} \mathcal{H}(\mathcal{L}) &= \begin{bmatrix} \dfrac{\partial^2 \mathcal{L}}{\partial \lambda^2} & \dfrac{\partial^2 \mathcal{L}}{\partial x \partial \lambda} \\[1em] \dfrac{\partial^2 \mathcal{L}}{\partial \lambda \partial x} & \dfrac{\partial^2 \mathcal{L}}{\partial x^2} \end{bmatrix} \\ &= \begin{bmatrix} \dfrac{\partial^2 \mathcal{L}}{\partial \lambda_1^2} & \cdots & \dfrac{\partial^2 \mathcal{L}}{\partial \lambda_1 \partial \lambda_m} & \dfrac{\partial^2 \mathcal{L}}{\partial \lambda_1 \partial x_1} & \cdots & \dfrac{\partial^2 \mathcal{L}}{\partial \lambda_1 \partial x_n} \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ \dfrac{\partial^2 \mathcal{L}}{\partial \lambda_m \partial \lambda_1} & \cdots & \dfrac{\partial^2 \mathcal{L}}{\partial \lambda_m^2} & \dfrac{\partial^2 \mathcal{L}}{\partial \lambda_m \partial x_1} & \cdots & \dfrac{\partial^2 \mathcal{L}}{\partial \lambda_m \partial x_n} \\ \dfrac{\partial^2 \mathcal{L}}{\partial x_1 \partial \lambda_1} & \cdots & \dfrac{\partial^2 \mathcal{L}}{\partial x_1 \partial \lambda_m} & \dfrac{\partial^2 \mathcal{L}}{\partial x_1^2} & \cdots & \dfrac{\partial^2 \mathcal{L}}{\partial x_1 \partial x_n} \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ \dfrac{\partial^2 \mathcal{L}}{\partial x_n \partial \lambda_1} & \cdots & \dfrac{\partial^2 \mathcal{L}}{\partial x_n \partial \lambda_m} & \dfrac{\partial^2 \mathcal{L}}{\partial x_n \partial x_1} & \cdots & \dfrac{\partial^2 \mathcal{L}}{\partial x_n^2} \\ \end{bmatrix} \\ &= \begin{bmatrix} 0_{m \times m} & \dfrac{\partial g}{\partial x} \\[1em] \left(\dfrac{\partial g}{\partial x} \right)^T & \dfrac{\partial^2 \mathcal{L}}{\partial x^2} \end{bmatrix} \end{align}\)

$0_{m \times m}$은 $m \times m$의 영행렬이며, $\dfrac{\partial g}{\partial x}$는 $m \times n$의 행렬이다. 이때, $\dfrac{\partial^2 \mathcal{L}}{\partial x^2}$는 $n \times n$의 헤시안 행렬이다.

따라서 Bordered Hessian 행렬은 $m+n$의 크기를 가진다.

기존의 Hessian 행렬의 definite을 사용해서 극대 극소를 판정했던 것 처럼, Bordered Hessian 행렬도 비슷하게 사용해서 원래 문제의 극대 극소를 판정할 수 있다. Bordered Hessian 행렬 자체는 언제나 indefinite 일 수 밖에 없는데, 이는 라그랑지안의 극점이 말안장점(saddle point)에 위치하기 때문이다. 그래서 조금 다른 방식으로 구해야 한다.

이전의 포스트에서 선행 주 소행렬식을 사용해서 definite을 정하는 방법을 약간 변형한다. $n$개의 변수와 $m$개의 제약조건이 있는 Bordered Hessian Matrix에 대해서 마지막으로부터 $n-m$개의 소행렬의 행렬식의 값을 조사하면 된다.

• local maximum이려면, 마지막 $n-m$개의 주 소행렬식의 부호가 제일 작은 소행렬식이 $(-1)^{m+1}$로 시작해서 교대로 나와야 한다.
• local minimum이려면, 마지막 $n-m$개의 주 소행렬식의 부호들이 전부 $(-1)^{m}$여야 한다.
• 둘 다 아니라면 indefinite로 말안장점이다.
• $m=0$인 경우는 제약없는 최적화 문제가 된다. Bordered Hessian 행렬은 Hessian 행렬이 되며, 이때는 Hessian 행렬의 definite를 사용하면 된다.

문제 자체가 Convex Problem인지 판별

목적함수와 제약 조건들의 교집합을 constrained surface 라 하기도 하는데, 이 constrained surface 자체가 convex면 그때의 극점은 반드시 극소점임이 보장된다.
즉, 이 문제 자체가 convex optimization 문제에 속한다면 극값이 곧 극소점이므로, 극값만 구해도 된다.

equality constrained minimizing 문제가 convex optimization 문제인지 판별하는 방법은 다음과 같다 :

1. 목적함수와 제약 조건들이 모두 convex function이어야 한다.
2. 제약 조건들이 affine function이어야 한다.
3. 제약 조건들이 linearly independent 해야 한다.
4. 제약 조건들이 convex set을 이루어야 한다.
5. 목적함수와 제약 조건들이 모두 differentiable 해야 한다.
6. Slater’s condition을 만족해야 한다. (이건 나중에 다루겠다)

이 조건들을 만족하면, 이 문제는 convex optimization 문제이며, 라그랑주 승수법을 사용한 후에 극점 판별을 생략할 수 있다. 위 조건들에 대한 자세한 내용은 다음을 참고하자

참고 3 : 모두를 위한 컨벡스 최적화 - Convex Sets
참고 4 : 모두를 위한 컨벡스 최적화 - Convex Functions

예시 1, 단순한 예시

일전의 최적화 소개 포스트에서 다뤘던 등식 제약을 가진 컨벡스 최적화 문제를 다시 보자

\[\begin{align} \text{minimize} \quad & f(x) = x_1^2 + x_2^2 \\ \text{subject to} \quad & g(x) = x_1 + x_2 - 1 = 0 \end{align}\]

위의 문제를 라그랑주 승수법을 사용해서 풀어보자.

라그랑주 승수법 사용

일단, 라그랑지안을 먼저 구성한다 :

\[\begin{align} \mathcal{L}(x, \lambda) &= f(x) + \lambda g(x) \\ &= x_1^2 + x_2^2 + \lambda(x_1 + x_2 - 1) \end{align}\]

다음으로, 라그랑지안의 그라디언트가 0인 지점들을 찾는다

\[\begin{align} \frac{\partial \mathcal{L}}{\partial x_1} &= 2x_1 + \lambda = 0 \label{eq1}\\ \frac{\partial \mathcal{L}}{\partial x_2} &= 2x_2 + \lambda = 0 \label{eq2}\\ \frac{\partial \mathcal{L}}{\partial \lambda} &= x_1 + x_2 - 1 = 0 \\ \nonumber \\ x_1 &= x_2, (\ref{eq1}) - (\ref{eq2}) \\ \therefore 2x_1 - 1 &= 0, x_1 = x_2 = \frac{1}{2} \end{align}\]

라그랑지안으로 찾아진 해는 극점인 것만 보장하므로, 이게 최소값인지 최대값인지 확인해야 한다. 이때, 제약 조건이 있는 최적화 문제에서는, 목적 함수의 헤시안 행렬이 positive definite이 아니더라도 제약 조건의 형태에 따라 최소값이 생길 수 있다.

따라서 이 해가 극소값인지 확인하기 위한 추가적인 절차가 필요하다.

극점 판별 1, Bordered Hessian Matrix

위 예시에서의 Bordered Hessian 행렬은 다음과 같다 :

\[\begin{align} \mathcal{H} &= \begin{bmatrix} \dfrac{\partial^2 \mathcal{L}}{\partial x_1^2} & \dfrac{\partial^2 \mathcal{L}}{\partial x_1 \partial x_2} & \dfrac{\partial^2 \mathcal{L}}{\partial x_1 \partial \lambda} \\ \dfrac{\partial^2 \mathcal{L}}{\partial x_2 \partial x_1} & \dfrac{\partial^2 \mathcal{L}}{\partial x_2^2} & \dfrac{\partial^2 \mathcal{L}}{\partial x_2 \partial \lambda} \\ \dfrac{\partial^2 \mathcal{L}}{\partial \lambda \partial x_1} & \dfrac{\partial^2 \mathcal{L}}{\partial \lambda \partial x_2} & \dfrac{\partial^2 \mathcal{L}}{\partial \lambda^2} \end{bmatrix} \\ &= \begin{bmatrix} 2 & 0 & 1 \\ 0 & 2 & 1 \\ 1 & 1 & 0 \end{bmatrix} \end{align}\]

이때 $\lvert \mathcal{H} \rvert = -4 < 0$ 이므로, $x^* = \left(\frac{1}{2}, \frac{1}{2}\right)$는 우리가 찾던 최소값, optimal solution이 맞다.

극점 판별 2, Convex Problem 판정

위의 예시는 모두 위의 조건을 만족하므로, 이 문제는 convex optimization 문제이다. 따라서, 위에서 찾은 해가 극소점임을 확인할 필요가 없다.

• 목적 함수의 헤시안 행렬은 언제나 positive definite이므로, convex function이다.
• 제약 조건 함수가 affine function 이며, 미분 가능하다.

라그랑주 승수법의 기하학적 의미

위의 예시 문제에서 라그랑주 승수법을 그림으로 표현해보자 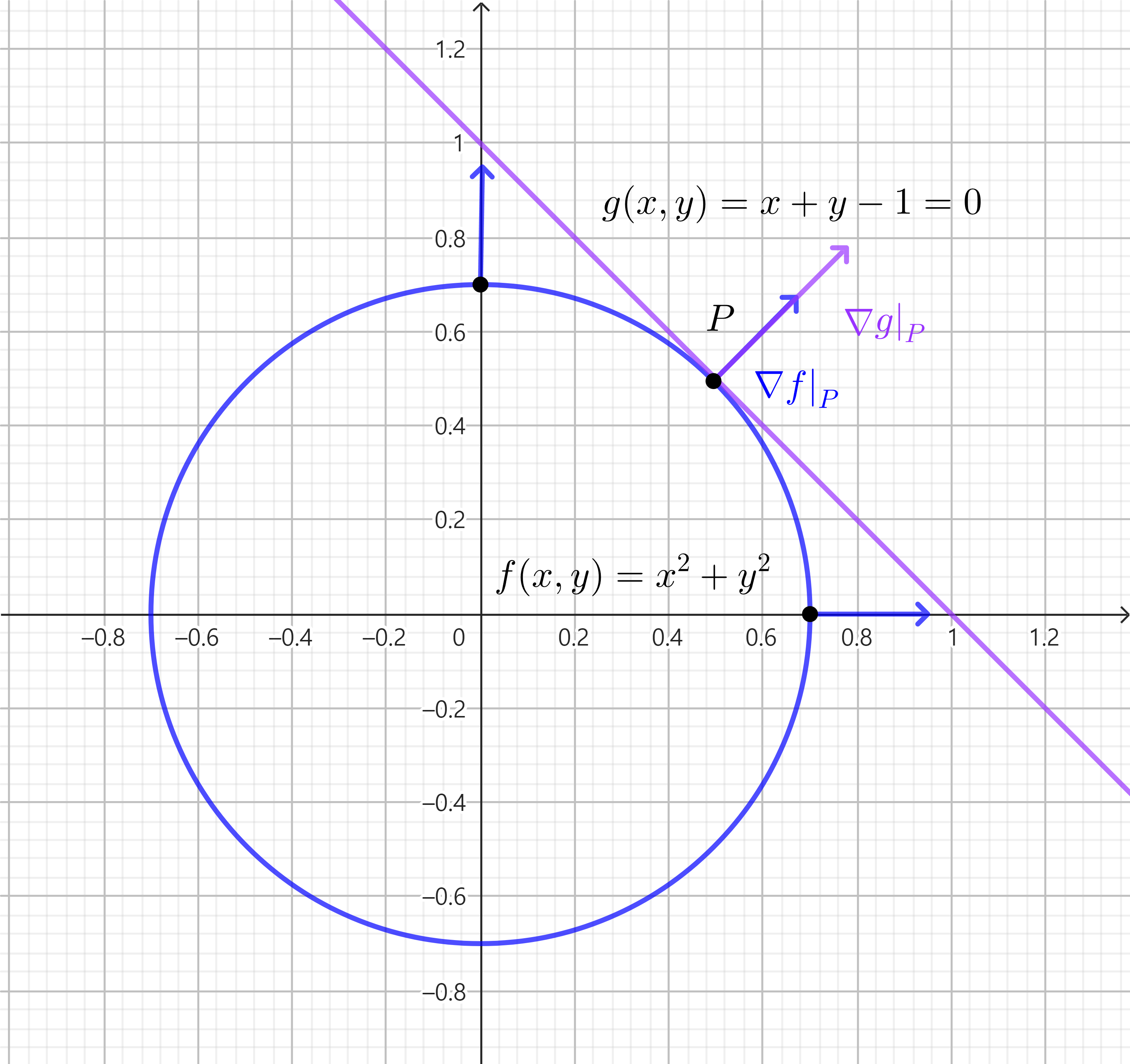목적함수와 제약조건과의 접점 & 그라디언트 벡터

목적 함수의 값을 $r^2$이라 하면, $f(x,y) = x^2 + y^2 = r^2$이 되어, 원점을 중심으로 반지름 $r$을 가진 원이 된다.

이때, 제일 작은 $r$을 가지면서, 제약조건 직선 $x + y = 1$과 만나는 점 $P$에서 최소값이 된다.
이 점은 목적함수의 등고선과 제약조건의 접점이 되며, 이 접점에서의 그라디언트 벡터는 서로 평행하게 된다.

이를 수식으로 나타내면, $\nabla f = \lambda \nabla g, \lambda \in \mathbb{R}$로 표현할 수 있으며, 이때의 $\lambda$가 라그랑주 승수(Lagrange multiplier)이다.

전미분을 사용한 라그랑주 승수법의 증명

참고 5 : Analytic proof of lagrange, MIT

라그랑주 승수법의 형태를 전미분을 사용해서 증명해보자.

어떤 실수 벡터 $x \in \mathbb{R}^n$, 함수 $f(x) : \mathbb{R}^n \rightarrow \mathbb{R}$, $m$개의 제약 조건들 $g_i(x) : \mathbb{R}^n \rightarrow \mathbb{R}, i = 1, 2, \cdots, m$이 주어졌다고 하자. 이 제약 최적화 문제의 최적해가 $x^* $ 로 존재한다 가정한다.

이때, $r(t) = \begin{bmatrix} x_1(t) & \cdots & x_n(t) \end{bmatrix}^T$를 constrained surface 상의 곡선이고, 변수 $t$로 파라미터화 되어있으며, $t=0$일때 optimal solution $x^* $인 곡선으로 정의하자.
즉, $r(0) = x^*$이며, constrained surface 상에 있으므로 $g_i(r(t)) = 0$도 만족한다.

이제 새로운 함수 $\hat{f}(t) = f(r(t))$를 정의하자. 이 함수는 $t=0$에서 최소값을 가지므로 미분하면 해당 지점에서 0이 되어야 한다.

$\hat{f}(t)$를 미분하면 다음과 같다 :

\[\begin{align} \frac{d \hat{f}(t)}{dt} &= \frac{\partial f}{\partial x_1} \frac{dx_1}{dt} + \cdots + \frac{\partial f}{\partial x_n} \frac{dx_n}{dt} \nonumber \\ &= \nabla f \cdot \begin{bmatrix} \dfrac{dx_1}{dt} \\ \vdots \\ \dfrac{dx_n}{dt} \end{bmatrix} = \nabla f \cdot r'(t) \nonumber \\ \nonumber \\ \text{As }& \left. \frac{d \hat{f}(t)}{dt} \right|_{t=0} =0, \quad \left. \nabla f \right|_{x^*} \cdot r'(0) = 0 \label{totaldiff_1}\\ \end{align}\]

따라서 $\nabla f(x^* )$는 $r’(0)$에 언제나 수직이므로 $x^*$에서 모든 곡선에 대해 수직이 된다.

다음으로 제약 조건들도 미분해보자. 새로운 함수 $\hat{g}_i(t) = g_i(r(t))$를 정의한다. 이 함수는 처음부터 constrained surface 상의 곡선 $r(t)$가 입력으로 들어가므로, 언제나 $\hat{g}_i(t)=0$이 된다. 양변을 $t$에 대해 미분해도 여전히 우변은 0이 된다.

이에 제약 조건 함수들을 한번에 합쳐서 표현하면 다음과 같다 :

\[\begin{align} \forall \hat{g}_i(t) &= 0 \Rightarrow \sum_{i=1}^{m} \lambda_i \hat{g}_i(t) = 0, \lambda_i \in \mathbb{R} \\ \frac{d}{dt}\left( \sum_{i=1}^{m} \lambda_i \hat{g}_i(t) \right) &= \sum_{i=1}^{m} \lambda_i \frac{d \hat{g}_i(t)}{dt} \nonumber \\ &= \left( \sum_{i=1}^{m} \lambda_i \nabla g_i \right) \cdot r'(t) \label{totaldiff_2}\\ \end{align}\]

따라서 $\sum \lambda_i \nabla g_i$은 언제나 $r’(t)$에 수직이며, $t=0$ 일 때도 여전히 수직이므로 $x^*$에서 모든 곡선에 대해 수직이다.

이제 $\ref{totaldiff_1}, \ref{totaldiff_2}$ 에 의해 $\nabla f(x^* )$와 $\sum \lambda_i \nabla g_i$는 서로 평행하므로 다음 관계가 성립하게 된다.

\[\nabla f(x^* ) + \sum \lambda_i \nabla g_i = 0, \lambda_i \in \mathbb{R}\]

이는 처음에 소개한 라그랑주 승수법의 형태와 동일하다.

예시 2, 무어-펜로즈 유사 역행렬 유도

라그랑주 승수법을 사용해서 무어-펜로즈 유사 역행렬의 성질들 중 하나를 유도해보자.

참고 : Penrose_inverse - Minimum norm solution to a linear system
참고 : Penrose_inverse - Linear least-squares

행보다 열이 큰 경우

행렬 $A \in \mathbb{R}^{m \times n}$, $m < n$, 벡터 $x \in \mathbb{R}^n$, $b \in \mathbb{R}^m$가 주어졌다고 하자. 이때, $Ax = b$를 만족하는 $x$를 찾는 문제를 풀어보자.

$A$가 정방행렬이 아니므로 $A^{-1}$는 정의되지 않는다. 그리고 위 등식을 만족하는 $x$는 무한히 많기 까지 하다.

이때, 무어-펜로즈 유사 역행렬을 사용하면, 위 등식을 만족하는 $x$ 중에서 가장 작은 $\lVert x \rVert^2_2$를 가지는 $x$로 결정지을 수 있는데, 다음과 같다 :

\[\begin{align} x = A^+b = A^T(A A^T)^{-1} b \end{align}\]

이제 라그랑주 승수법을 사용해서 위 형태를 유도해보자.

위 문제를 등식 제약을 가진 최적화 문제로 표현하면 다음과 같다 :

\[\begin{align} \text{minimize} \quad & ||x||^2_2=x^Tx \\ \text{subject to} \quad & Ax = b \end{align}\]

목적 함수가 convex function이고, 제약 조건이 affine function에 differentiable하므로, 위 문제는 convex optimization 문제가 된다. 별도의 극값 판정 없이 최소화 문제의 optimal solution 임을 알 수 있다.

라그랑지안으로 변환해서 편미분하면 다음과 같다 :

\[\begin{align} \mathcal{L}(x, \lambda) &= x^T x + \lambda^T(Ax - b) \\ \frac{\partial \mathcal{L}}{\partial x} &= 2x + A^T \lambda = 0 \\ \frac{\partial \mathcal{L}}{\partial \lambda} &= Ax - b = 0 \\ \nonumber \\ \Rightarrow & 2Ax + A A^T \lambda = 0, \\ & 2Ax-2b = 0 \\ \Rightarrow & \lambda = -2(A A^T)^{-1} b \\ \nonumber \\ \therefore x &= A^T(A A^T)^{-1}b \end{align}\]

이는 무어-펜로즈 유사 역행렬의 결과와 동일하다.

행보다 열이 작은 경우

이번에는 행렬 $A \in \mathbb{R}^{m \times n}$, $m > n$, 벡터 $x \in \mathbb{R}^n$, $b \in \mathbb{R}^m$가 주어졌다고 하자. 이때, $Ax = b$를 최대한 만족하는 $x$를 찾는 문제를 풀어보자.

이때, 무어-펜로즈 유사 역행렬을 사용하면, $Ax$와 $b$의 오차제곱합이 제일 작은 $x$를 찾을 수 있으며 다음과 같다 :

\[\begin{align} x = A^+b = (A^TA)^{-1}A^Tb \end{align}\]

이 내용을 최적화 문제로 옮기면 다음과 같다 :

\[\begin{align} \text{minimize} \quad f(x)=\lVert Ax-b \rVert^2_2=(Ax-b)^T(Ax-b) \\ \end{align}\]

문제의 목적함수의 Hessian matrix는 다음과 같다 :

\[\begin{align} \left( \frac{\partial f}{\partial x} \right)^T &= 2A^T(Ax-b) \\ \frac{\partial^2 f}{\partial x^2} &= \frac{\partial}{\partial x} \left( 2A^T(Ax-b) \right) \nonumber \\ &= 2A^TA = \mathcal{H}\\ \nonumber \\ x^T \mathcal{H} x &= x^T 2A^TA x \nonumber \\ &= 2(Ax)^T(Ax) \nonumber \\ &= 2\lVert Ax \rVert^2_2 >= 0 \end{align}\]

$\mathcal{H}$가 positive semidefinite 이므로 목적함수는 convex function이다. 따라서 이 문제는 convex optimization 문제이며 편미분 해서 찾아낸 극점이 바로 global minimum이 된다.

이제 목적함수를 편미분하여 극점을 찾으면 다음과 같다 :

\[\begin{align} \frac{\partial f}{\partial x} &= 2A^T(Ax-b) = 0 \\ \Rightarrow & A^TAx = A^Tb \\ \Rightarrow & x = (A^TA)^{-1}A^Tb \end{align}\]

이는 무어-펜로즈 유사 역행렬의 결과와 동일하다.