회전 행렬의 수학적 특성
이번 포스트는 왜 회전 행렬이 다음의 성질을 가지는지에 대한 내용이다.
\[\begin{equation} R^{-1} = R^T \end{equation}\]단순 계산으로 증명
기존의 $R(\theta) = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix}$ 를 가지고 단순 계산하여 저 특성을 증명해 보자
\[\begin{split} R^{-1} &= \frac{1}{\cos^2{\theta}+\sin^2{\theta}} \begin{bmatrix} \cos(\theta) & \sin(\theta) \\\ -\sin(\theta) & \cos(\theta) \end{bmatrix} \\[10pt] &= \begin{bmatrix} \cos(\theta) & \sin(\theta) \\\ -\sin(\theta) & \cos(\theta) \end{bmatrix} \\[10pt] &= R^T \end{split}\]따라서 $R^{-1} = R^T$ 가 된다.
좌표계 축 벡터의 변환으로 증명
그림1 : 회전된 좌표축의 벡터값
회전된 좌표의 축 벡터와 회전 행렬의 관계
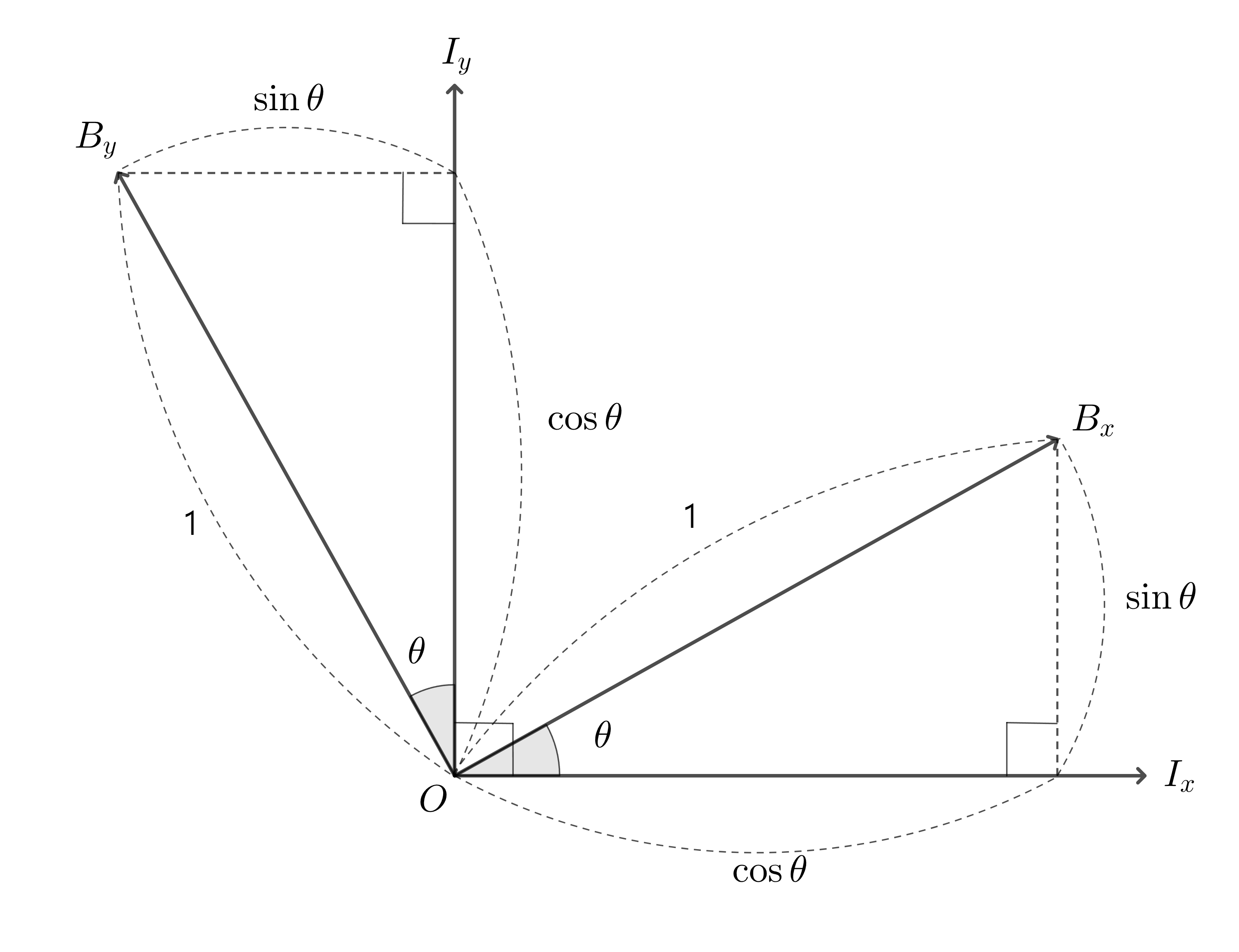
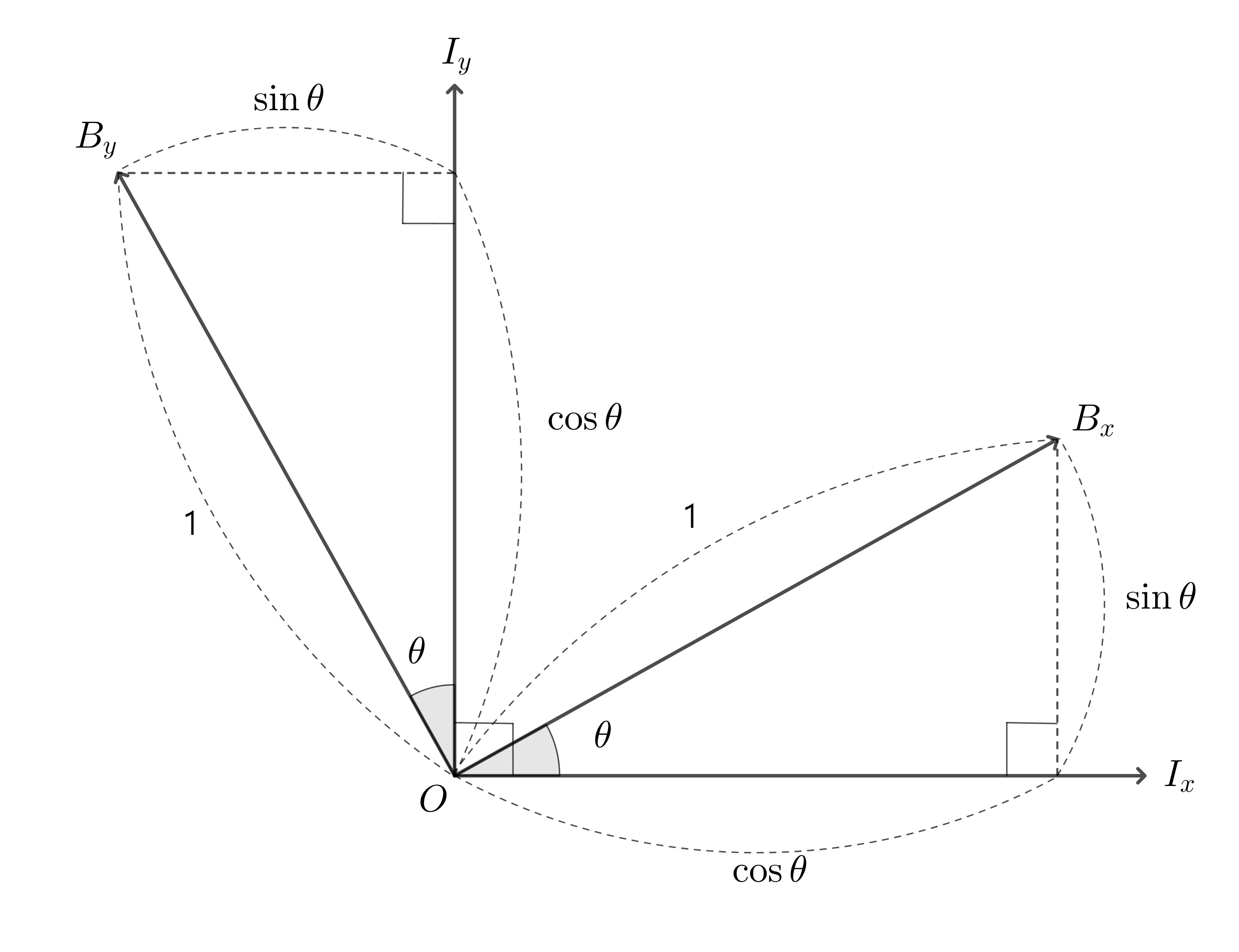
위 그림1 에서 $Ri_x = b_x, Ri_y = b_y$가 된다. 이때 $I$ 프레임의 실제 축 벡터들의 값은 $i_x = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, i_y = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$ 이 된다.
그러므로, $Ri_x = b_x$라는 것은 실제로는 $R\begin{bmatrix} 1 \\ 0 \end{bmatrix} = b_x$임을 의미한다. 이는 회전행렬 $R$의 왼쪽 행 벡터가 바로 $b_x$ 임을 보여준다.
비슷하게, $Ri_y = b_y$라는 것은 실제로는 $R\begin{bmatrix} 0 \\ 1 \end{bmatrix} = b_y$임을 의미한다. 이는 회전행렬 $R$의 오른 행 벡터가 바로 $b_y$ 임을 보여준다.
정리하면 다음과 같다.
\[\begin{align} R &= \left[\begin{array}{c|c} b_x & \begin{array}{c} ? \\ ? \end{array} \end{array} \right] \\[10pt] R &= \left[\begin{array}{c|c} \begin{array}{c} ? \\ ? \end{array} & b_y \end{array} \right] \end{align}\]기준 좌표계 $I$ 에서 $\theta$ 만큼 회전된 좌표계의 $x,y$ 축벡터를 $b_x, b_y$라 할 때,
\[\begin{equation} \therefore R = \left[\begin{array}{c|c} b_x & b_y \end{array}\right] \label{e1} \end{equation}\]
벡터를 $\theta$ 만큼 회전시키는 회전 행렬 $R(\theta)$는 다음과 같다.
이 사실을 회전 행렬의 유도에 그대로 적용해 보자.
그림 1을 보자. I 좌표계에서 B 좌표계의 각각의 축 벡터의 값은 다음과 같다
\[\begin{align} b_x &= \begin{bmatrix} \cos{\theta} \\ \sin{\theta} \end{bmatrix} \\[10pt] b_y &= \begin{bmatrix} -\sin{\theta} \\ \cos{\theta} \end{bmatrix} \end{align}\]따라서 이를 다시 식 $\eqref{e1}$에 넣으면 다음과 같다
\[\begin{equation} R(\theta) = \left[ \begin{array}{c|c} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{array} \right] \end{equation}\]임의의 벡터와 축의 회전 변환
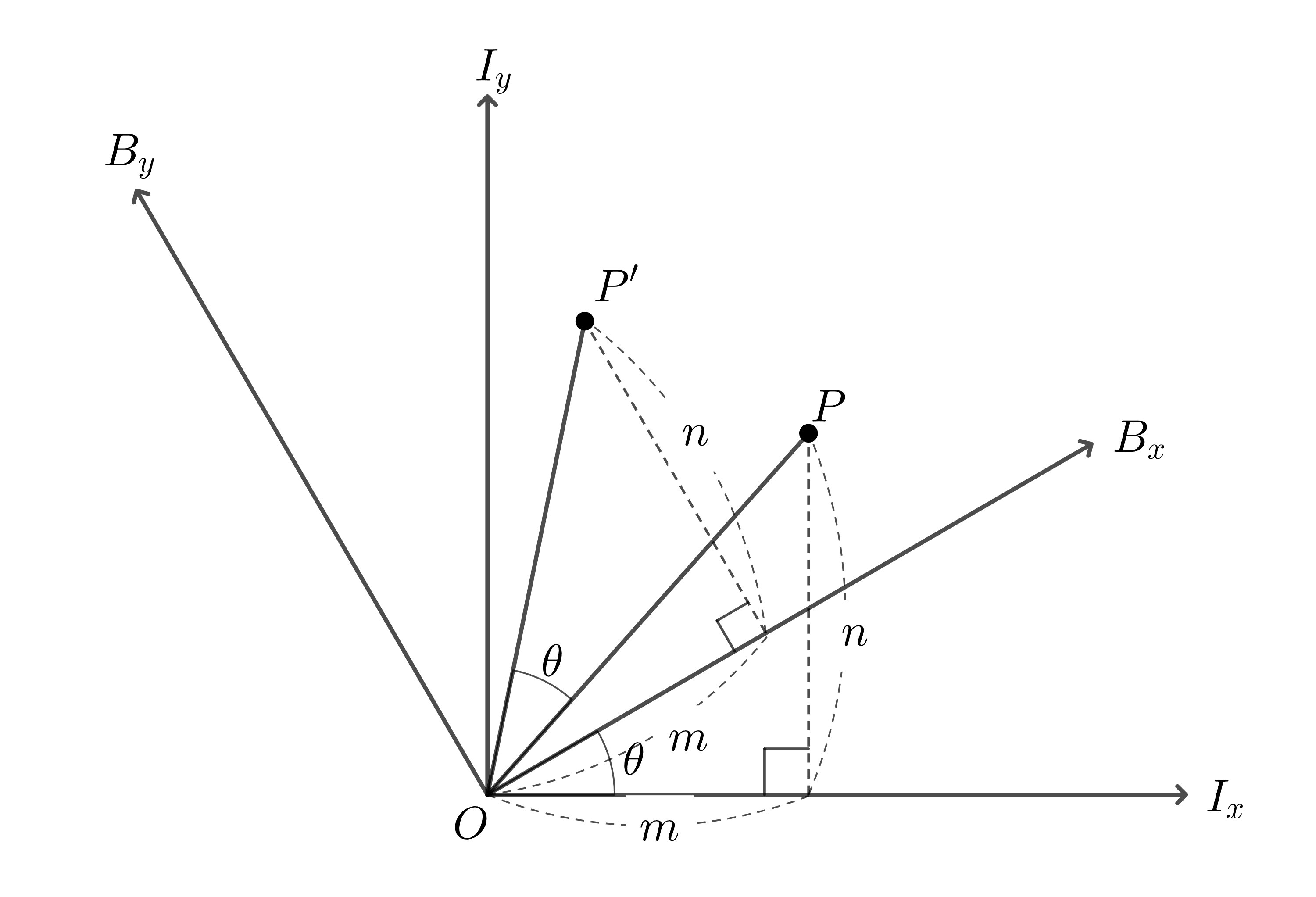그림2 : 선형 결합의 배수는 유지하면서 기저 벡터만 변환된다
이를 이해하고 다시 $R(\theta)P = P’$ 식을 보자. 그림2의 점 P는 다음과 같이 2개의 축 벡터의 선형 결합으로 표현될 수 있다.
수식으로 표현하면 다음과 같다.
이제 점 $P$에 회전 변환 $R(\theta)$를 곱하면 어떻게 될까.
\[\begin{align} R(\theta)P &= R(\theta)\left( m i_x + n i_y \right) \nonumber \\[5pt] &= m R(\theta) i_x + n R(\theta) i_y \nonumber \\[5pt] &= m \left[ \begin{array}{c|c} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{array} \right] \begin{bmatrix} 1 \\ 0 \end{bmatrix} + n \left[ \begin{array}{c|c} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{array} \right] \begin{bmatrix} 0 \\ 1 \end{bmatrix} \nonumber \\[10pt] &= m \begin{bmatrix} \cos{\theta} \\ \sin{\theta} \end{bmatrix} + n \begin{bmatrix} -\sin{\theta} \\ \cos{\theta} \end{bmatrix} \nonumber \\[10pt] &= m b_x + n b_y \label{e2} \end{align}\]결과 식 \eqref{e2} 를 통해 회전 변환의 의미를 다시 생각해 볼 수 있다.
임의의 점 $P$를 해당 좌표계의 축 벡터들의 선형 결합으로 분해한 다음, 회전 행렬 $R(\theta)$를 곱하여 축 벡터만 정확하게 회전된 좌표계의 축 벡터로 바꾸는 변환이었던 것이다.
여기까지 오고 나면, 굳이 회전 뿐만 아니라 온갖 종류의 다양한 변환에 대한 행렬 역시 어떤 모양이 될 지 예상해 볼 수 있다. 예를 들면 y=0 축에 대한 대칭 변환 등이 있다.
$R^{-1}=R^T$ 의 증명
앞서 $\eqref{e1}$에서 $R = \left[\begin{array}{c|c} b_x & b_y \end{array}\right]$ 임을 보였다.
이때, $b_x$와 $b_y$ 역시 직교좌표계의 좌표축이므로 다음 성질을 만족한다.
따라서 다음과 같다.
\[\begin{align} R^T R &= \left[\begin{array}{cc} b_x^T \\[5pt] \hline b_y^T \end{array} \right] \left[\begin{array}{c|c} b_x & b_y \end{array}\right] \nonumber \\[15pt] &= \begin{bmatrix} b_x^T b_x & b_x^T b_y \\[5pt] b_y^T b_x & b_y^T b_y \end{bmatrix} \nonumber \\[15pt] & = \begin{bmatrix} \vec{b_x}\cdot\vec{b_x} & \vec{b_x}\cdot\vec{b_y} \\ \vec{b_y}\cdot\vec{b_x} & \vec{b_y}\cdot\vec{b_y} \end{bmatrix} \nonumber \\[15pt] &= \begin{bmatrix} \left\Vert\vec{b_x}\right\Vert^2 & 0 \\ 0 & \left\Vert \vec{b_y} \right\Vert^2\end{bmatrix} \nonumber \\[20pt] \therefore R^T R &= \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix} = I \end{align}\] \[\begin{align} R^TR &= I \nonumber \\ (R^T)^{-1} \left( R^T R \right) R^T &= (R^T)^{-1} I R^T, \text{if } (R^T)^{-1} \text{ exists} \nonumber \\ \left( (R^T)^{-1} R^T\right) (R R^T) &= I \nonumber \\ \therefore R R^T &= I \label{e3} \end{align}\]따라서 $RR^T = R^TR = I$ 이므로, 이는 역행렬의 정의에 해당된다. \(\begin{align} \therefore R^T &= R^{-1} \end{align}\)
선형 변환의 특성으로 증명
앞서 회전 변환은 선형 변환의 한 부분이라 했다. 또한 모든 선형 변환들을 행렬로 나타낼 수 있다 하였다.
공학도의 입장에서 좌표계=벡터공간, 축벡터=단위 기저벡터 정도로 생각해도 된다(물론 완전히 동일한 것은 아니다)
$2\times2$ 행렬 $R$은 임의의 2개의 기저 벡터 $\vec{a}, \vec{b}$를 각각 새로운 2개의 기저 벡터 $\vec{a’}, \vec{b’}$로 변환한다.
이는 자연스럽게 확장이 가능하며, 만약 $3\times3$ 행렬 $R_3$ 였다면, 임의의 3개의 기저 벡터 $\vec{a}, \vec{b}, \vec{c} -> \vec{a’}, \vec{b’}, \vec{c’}$로 변환 된다.
이렇게 $n\times n$ 행렬 까지 확장이 가능하다.
그래서 회전 행렬 $R$로 $i_x, i_y -> b_x, b_y$ 변환이 가능 했던 것이다.
재미있는 점은, 결과물인 $b_x, b_y$ 벡터가 꼭 식 $\eqref{e0}$ 회전 변환의 특성을 만족할 필요는 없다는 것이다.
$b_x, b_y$를 어떻게 정하느냐에 따라, 좌표계를 뒤집고, 기울이고, 늘리고, 회전시킬 수 있다.
회전 변환 행렬의 조건
그렇다면 $2\times 2$, 또는 $3\times3$행렬 R에 대해서 수많은 좌표계 선형 변환이 가능한데, 그 중에서 회전 변환만이 가지는 특성은 무엇일까?
크게 다음 2가지가 있다.
- 변환 전과 변환 후의 벡터의 길이가 변하지 않음
- 변환 전과 변환 후의 두 벡터의 각도가 보존됨
임의의 벡터 $x \in \mathbb{R}^n$에 대해 1번 조건을 수식으로 표현하여 조건을 찾아내면 다음과 같다.
\[\begin{align} \left\Vert x \right\Vert^2 &= \left\Vert Rx \right\Vert^2 \\ x^T x &= \left(Rx\right)^T Rx \nonumber \\ x^T x & = x^T R^T R x \nonumber \\ \therefore R^T R &= I \end{align}\]임의의 벡터 $a,b \in \mathbb{R}^n$ 에 대해 2번 조건 역시 수식으로 표현하여 조건을 찾아내면 다음과 같다.
\[\begin{align} \vec{a} \cdot \vec{b} &= \vec{Ra} \cdot \vec{Rb} \\ a^T b &= \left(Ra \right)^T Rb \nonumber \\ a^T b &= a^T R^T R B \nonumber \\ \therefore R^T R &= I \end{align}\]따라서 위의 식 $\eqref{e3}$ 에 의해서 $R^{-1} = R^T$ 이다.
하지만 아직 부족하다
회전 행렬과 거울 대칭 행렬의 구분
가만히 생각해보면, 회전 행렬 이외에도 위의 2가지 성질을 전부 만족하는 행렬이 하나 더 있는데, 바로 거울 대칭 행렬이다.
그림3 : 대칭 변환과 각도의 보존
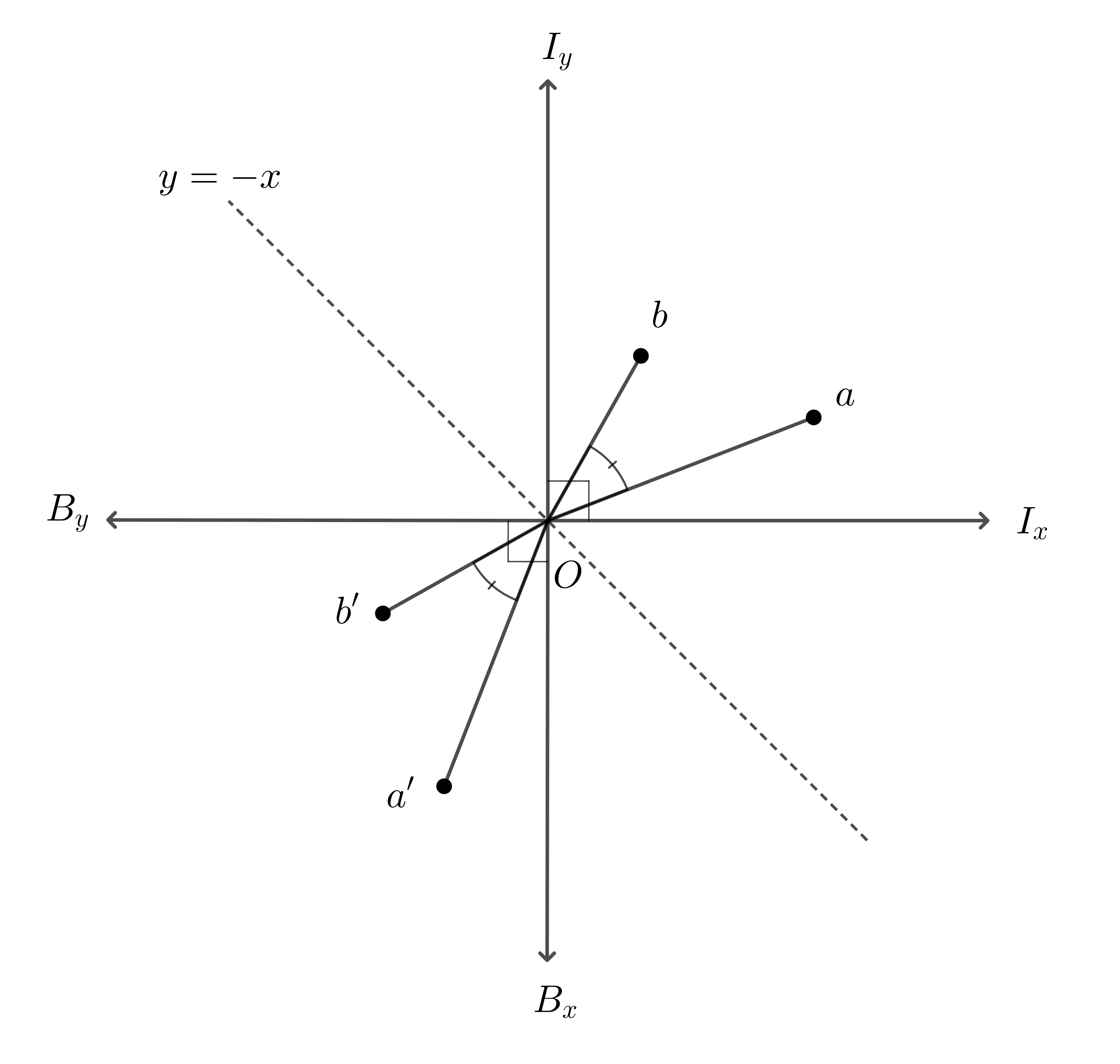
그림3 에서 보면, 임의의 축에 대해 거울 대칭된 벡터 $a’, b’$ 역시 조건1과 조건2를 전부 만족한다.
따라서, $R^{-1} = R^T$ 라는 조건에는 거울 대칭 행렬 역시 해당되는 샘이다.
예시로, 그림3은 $y=-x$ 축에 대칭 변환이며, 이때의 대칭 변환 행렬 $S$는 다음과 같다.
식 $\eqref{e1}$을 통해 유도할 수 있으며, 계산은 생략한다.
그리고 $S^{-1} = S^T$ 조건도 만족한다. 하지만 회전 행렬은 아니다. 이 둘을 구분하기 위해 또다른 조건이 필요한데, 다음과 같다
- 회전 행렬 R의 행렬식 값이 1이다, $det(R) = 1$
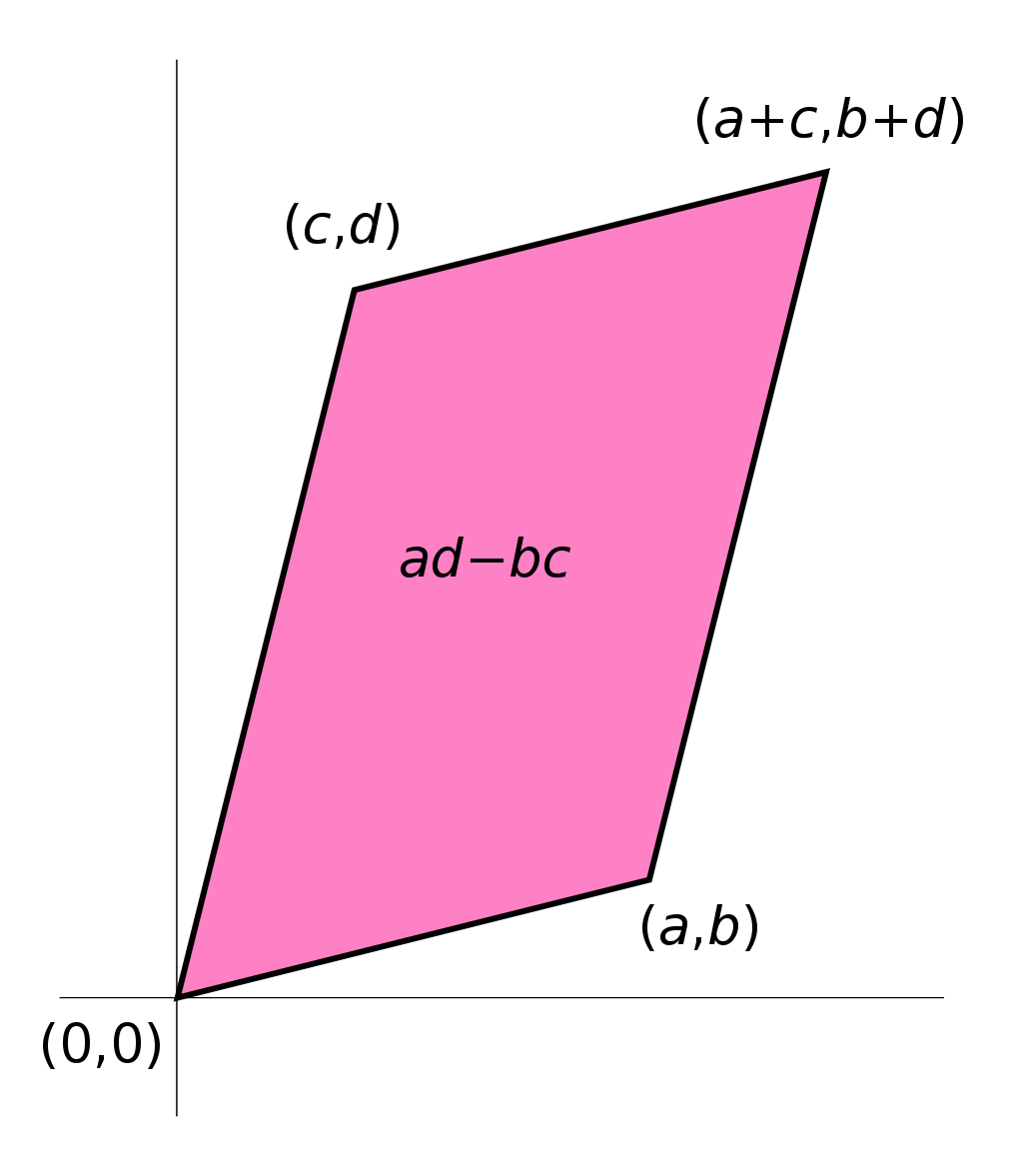
행렬식의 기하학적 의미는, 변환 전의 벡터쌍으로 이루어진 면적, 또는 부피가 변환 후에 어떻게 변하는지에 대한 비율이다. 2차원 행렬에서는 두개의 벡터로 표현된 평행사변형의 넓이. 3차원 행렬에서는 3개의 벡터로 표현된 평행육면체의 부피가 변하는 것의 비율이다.
이때 행렬식의 결과가 양수면 방향이 뒤집히지 않으며, 음수면 방향이 뒤집힘을 의미한다.
따라서 $det(R)$ 이 1 또는 -1 이라는 것은 변환 전과 후의 길이가 동일함을 의미하며 그 중에서도 $det(R) = 1$ 이라는 것은 방향이 뒤집히지 않음을 의미하므로 이는 회전 행렬의 조건이 된다.
참고1 : Determinant#Geometric meaning
참고2 : 3Blue1Brown - The determinant | Chapter 6, Essence of linear algebra
$R^{-1} = R^T$ 로부터 $det(R) = \pm 1$ 임을 유도할 수 있다.
행렬식 (det)연산은 다음의 성질을 만족한다.
- $det(A) = det(A^T)$
- $det(AB) = det(A) det(B)$
이를 이용하여 다음과 같이 유도된다.
\[\begin{align} R^{-1}R&=I \nonumber \\ det(R^{-1} R) &= det(I) \nonumber \\ det(R^T R) &= 1 \nonumber \\ det(R^T) det(R) &= 1 \nonumber \\ det(R)^2 &= 1 \nonumber \\ \therefore det(R) &= \pm 1 \end{align}\]이떄, $det(R) = -1$인 것은 변환 후의 면적(또는 부피)가 뒤집힘을 의미하므로, 거울 대칭이다.
따라서, 일반적인 회전 행렬(2,3차원)의 최종적인 정의는 다음과 같다.
\[\begin{align} \text{where }R \in \mathbb{R}^{2\times2} \text{ or } R \in \mathbb{R}^{3\times3} \nonumber \\ \text{if }R^{-1} = R^T \text{ & } det(R) = 1, \nonumber \\ \text{than, }R \in SO(2) \text{ } or \text{ } R \in SO(3) \end{align}\]
참고3 : $v \in \mathbb{R}^n$은 모든 $n$차원 실수 벡터 $v$를 의미한다.
참고4 : $A \in \mathbb{R}^{n \times m}$은 모든 $n \times m$ 실수 행렬 $A$를 의미한다.
$SO(2)$와 $SO(3)$는 Special Orthogonal Group으로써, Lie Group에서 다루는 군으로, 보통 회전 행렬에 대한 군으로 잘 알려져 있다.
$SO(2)$는 2차원 회전 행렬이며, $SO(3)$는 3차원 회전 행렬에 집합 내지 군으로 볼 수 있다.