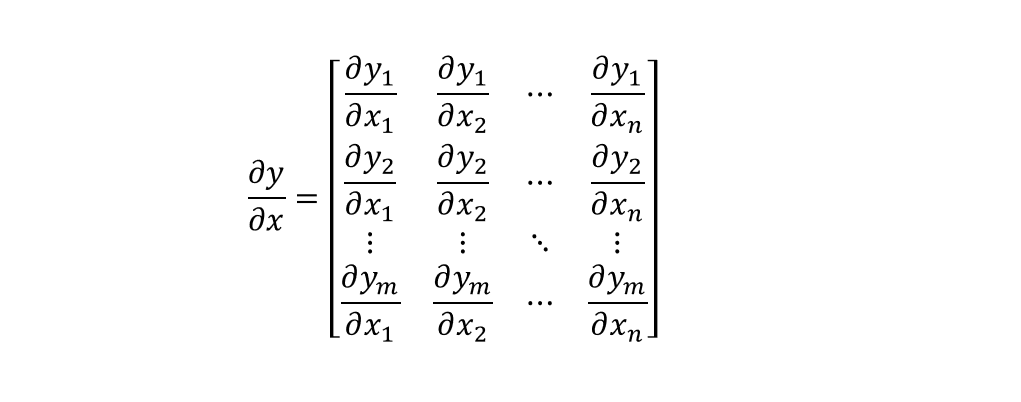행렬 미분

스칼라-벡터, 스칼라-행렬, 벡터-벡터 끼리의 편미분에 대하여.

참고 : Matrix calculus

행렬 미분이란

수학에서 행렬 미분이란 다변수 미적분학에서 사용하는 표기법이며, 특히 다변수의 편미분에 대한 표기를 다룬다. 기존의 변수가 하나 뿐이던 함수의 미분과 나름 유사한 편미분 법칙을 가지고 있다.

결과물이 행렬의 형태로 나오는 모든 편미분에 대한 표기와 미분 법칙에 대해 다루며, 다음의 조합이 가능하다

• 스칼라/스칼라
• 스칼라/벡터
• 스칼라/행렬
• 벡터/스칼라
• 벡터/벡터
• 행렬/스칼라

이는 다변수 함수의 Gradient와도 깊은 관련이 있고.
특히 최적화 분야에서는 다변수 함수의 Gradient에 관련된 연산이 매우 흔하기 때문에 필수적으로 알아야 한다.

예를 들어, 3개의 변수 $a,b,c \in \mathbb{R}$로 구성된 다변수 함수 $f(a,b,c)$가 있다고 하자. 이 함수의 gradient는 다음과 같이 표기된다

\[\begin{align} \nabla f = \frac{\partial f}{\partial a} \hat{a} + \frac{\partial f}{\partial b} \hat{b} + \frac{\partial f}{\partial c} \hat{c} \end{align}\]

이를 일종의 벡터로 생각해보면, 이렇게 표기할 수도 있다.

\[\begin{align} \nabla f &= \begin{bmatrix} \frac{\partial f}{\partial a} \\ \frac{\partial f}{\partial b} \\ \frac{\partial f}{\partial c} \end{bmatrix} \label{gradient-row}\\ \\ \text{if} \begin{bmatrix}a \\ b \\ c \end{bmatrix} &= \vec{x} \\ \frac{\partial f}{\partial x} &= \begin{bmatrix} \frac{\partial f}{\partial a} \\ \frac{\partial f}{\partial b} \\ \frac{\partial f}{\partial c} \end{bmatrix} \text{or, } \begin{bmatrix} \frac{\partial f}{\partial a} & \frac{\partial f}{\partial b} & \frac{\partial f}{\partial c} \end{bmatrix} \label{vector-column} \end{align}\]

표기법과 Layout

다음 내용에서는 스칼라, 벡터, 행렬을 모두 다루기 위해서 다음 표기법을 사용하겠다.

• 스칼라 : 그냥 소문자 ($a,b,c,x,y$)
• 벡터 : 볼드체 소문자 ($\mathbf{a,b,c,x,y}$)
• 행렬 : 대문자 볼드체 ($\mathbf{A,B,C,X,Y}$)

기본적으로 모든 벡터의 행렬 방향은 column vector를 기본으로 한다. 만약 row vector 방향으로 바꾸고 싶다면, $\mathbf{x}^T$로 표기한다. (transpose)

행렬 미분을 하면서, 분자와 분모의 성분이 어느 방향으로 전개되는지 정해줘야 하는데, 이를 Layout 이라 한다.
이때, 분자가 아래방향으로 써지면 Numerator layout, 옆으로 써지면 Denominator layout 이라고 한다. 분모는 분자와 반대 방향으로 전개된다.

위의 예시에서 Gradient 벡터를 아래로 길게 쓴 방향은 ($\ref{gradient-row}$), 분모의 방향이 아래로 향한 것이므로 분자의 방향은 옆으로 써지는 것이다. 따라서 Numerator Layout 이다.(또는 Jacobian Formulation 이라고도 한다)

반대로, 위의 예시에서 vector로 편미분한 결과물을 옆으로 길게 쓴 방향은 ($\ref{vector-column}$) 분모의 방향이 옆으로 써진 것이므로 분자의 방향은 아래로 써진 것이다. 따라서 Denominator Layout 이다. (또는 Hessian Formulation 이라고도 한다)

행렬 미분 - 스칼라

스칼라 / 스칼라

두 개의 스칼라 $a,b$에 대한 행렬 미분은 다음과 같다

\[\begin{align} \frac{\partial a}{\partial b} \end{align}\]

그냥 하던대로 하면 된다.

벡터 / 스칼라

벡터 $\mathbf{x} = \begin{bmatrix}x_1 & x_2 & \cdots & x_n\end{bmatrix}^T$ 에 대해서 :

\[\begin{align} \frac{\partial \mathbf{x}}{\partial a} &= \begin{bmatrix} \dfrac{\partial x_1}{\partial a} \\[1em] \dfrac{\partial x_2}{\partial a} \\ \vdots \\ \dfrac{\partial x_n}{\partial a} \end{bmatrix}, \text{(Numerator Layout)} \\ &= \begin{bmatrix} \dfrac{\partial x_1}{\partial a} & \dfrac{\partial x_2}{\partial a} & \cdots & \dfrac{\partial x_n}{\partial a} \end{bmatrix}, \text{(Denominator Layout)} \end{align}\]

어떠한 스칼라에 대해 편미분된 벡터를 Tangent Vector 라고도 한다.

행렬 / 스칼라

행렬 $\mathbf{A} \in \mathbb{R}^{p \times q}$에 대해서 :

\[\begin{align} \frac{\partial \mathbf{A}}{\partial a} &= \begin{bmatrix} \dfrac{\partial A_{11}}{\partial a} & \dfrac{\partial A_{12}}{\partial a} & \cdots & \dfrac{\partial A_{1q}}{\partial a} \\[1em] \dfrac{\partial A_{21}}{\partial a} & \dfrac{\partial A_{22}}{\partial a} & \cdots & \dfrac{\partial A_{2q}}{\partial a} \\[1em] \vdots & \vdots & \ddots & \vdots \\[1em] \dfrac{\partial A_{p1}}{\partial a} & \dfrac{\partial A_{p2}}{\partial a} & \cdots & \dfrac{\partial A_{pq}}{\partial a} \end{bmatrix}, \text{(Numerator Layout)} \\ &= \begin{bmatrix} \text{Numerator Layout} \end{bmatrix}^T, \text{(Denominator Layout)} \end{align}\]

어떠한 스칼라에 의해 편미분된 행렬을 Tangent Matrix 라고도 한다.

행렬 미분 - 벡터

스칼라 / 벡터

스칼라를 벡터로 편미분 하는 것은 다음과 같다.
벡터 $\mathbf{x} = \begin{bmatrix}x_1 & x_2 & \cdots & x_n\end{bmatrix}^T$ 에 대해서 :

\[\begin{align} \frac{\partial a}{\partial \mathbf{x}} &= \begin{bmatrix} \dfrac{\partial a}{\partial x_1} & \dfrac{\partial a}{\partial x_2} & \cdots & \dfrac{\partial a}{\partial x_n} \end{bmatrix}, \text{(Numerator Layout)} \\ &= \begin{bmatrix} \dfrac{\partial a}{\partial x_1} \\[2ex] \dfrac{\partial a}{\partial x_2} \\ \vdots \\ \dfrac{\partial a}{\partial x_n}\end{bmatrix}, \text{(Denominator Layout)} \end{align}\]

각각에 대해서 쓸모가 있는 layout이다.

예를 들어서, $f=f(a,b,c)$인 다변수 함수이고, $\mathbf{x}=\begin{bmatrix}a & b & c\end{bmatrix}^T$인 벡터. $a,b,c$는 각각 $t$에 대한 변수라면, 전미분(total differential)을 사용해서 $df/dt$ 는 다음과 같다 :

\[\begin{align} \frac{df}{dt} &= \frac{\partial f}{\partial a}\frac{da}{dt} + \frac{\partial f}{\partial b}\frac{db}{dt} + \frac{\partial f}{\partial c}\frac{dc}{dt} \\ &= \begin{bmatrix}\dfrac{\partial f}{\partial a} & \dfrac{\partial f}{\partial b} & \dfrac{\partial f}{\partial c}\end{bmatrix} \begin{bmatrix} \dfrac{da}{dt} \\[1em] \dfrac{db}{dt} \\[1em] \dfrac{dc}{dt} \end{bmatrix} \\ &= \frac{\partial f}{\partial \mathbf{x}} \frac{\partial \mathbf{x}}{\partial t}, \text{(Numerator Layout)} \end{align}\]

반면에 위 다변수 함수 $f$의 Gradient를 구한다고 하면 :

\[\begin{align} \nabla f = \begin{bmatrix} \dfrac{\partial f}{\partial a} \\[1em] \dfrac{\partial f}{\partial b} \\[1em] \dfrac{\partial f}{\partial c} \end{bmatrix} &= \left(\frac{\partial f}{\partial \mathbf{x}}, \text{(Numerator Layout)}\right)^T \\ &= \left( \frac{\partial f}{\partial \mathbf{x}}, \text{(Denominator Layout)} \right) \end{align}\]

으로 표기할 수 있기 때문에, Denominator Layout도 간간히 쓰인다.

이 외의 대부분의 상황에선 Numerator Layout이 많이 쓰인다.

벡터 / 벡터

두개의 벡터 $\mathbf{x} \in \mathbb{R}^n, \mathbf{y} \in \mathbb{R}^m$ 에 대해서 :

\[\begin{align} \frac{\partial \mathbf{y}}{\partial \mathbf{x}} &= \begin{bmatrix} \dfrac{\partial y_1}{\partial x_1} & \dfrac{\partial y_1}{\partial x_2} & \cdots & \dfrac{\partial y_1}{\partial x_n} \\[1em] \dfrac{\partial y_2}{\partial x_1} & \dfrac{\partial y_2}{x_2} & \cdots & \dfrac{\partial y_2}{\partial x_n} \\[1em] \vdots & \vdots & \ddots & \vdots \\[1em] \dfrac{\partial y_m}{\partial x_1} & \dfrac{\partial y_m}{\partial x_2} & \cdots & \dfrac{\partial y_m}{\partial x_n} \end{bmatrix}, \text{(Numerator Layout)} \\ &= \begin{bmatrix}\text{Numerator Layout}\end{bmatrix}^T, \text{(Denominator Layout)} \end{align}\]

이때 Numerator Layout으로 구성된 행렬을 Jacobian matrix라 한다.
벡터 미적분학에서, Jacobian 행렬은 다음과 같다 :

\[\begin{align} J = \begin{bmatrix} \frac{\partial \mathbf{f}}{\partial x_1} & \cdots &\frac{\partial \mathbf{f}}{\partial x_n}\end{bmatrix} &= \begin{bmatrix} \nabla^T f_1 \\ \vdots \\ \nabla^T f_m \end{bmatrix} = \begin{bmatrix}\frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n}\end{bmatrix} \\ &= \frac{\partial \mathbf{f}}{\partial \mathbf{x}}, \text{(Numerator Layout)} \end{align}\]

참조 : Jacobian Matrix

행렬 미분 - 행렬

스칼라 / 행렬

행렬 $\mathbf{A} \in \mathbb{R^{p \times q}}$ 에 대해서 :

\[\begin{align} \frac{\partial a}{\partial \mathbf{A}} &= \begin{bmatrix} \dfrac{\partial a}{\partial A_{11}} & \dfrac{\partial a}{\partial A_{21}} & \cdots & \dfrac{\partial a}{\partial A_{p1}} \\[1em] \dfrac{\partial a}{\partial A_{12}} & \dfrac{\partial a}{\partial A_{22}} & \cdots & \dfrac{\partial a}{\partial A_{p2}} \\[1em] \vdots & \vdots & \ddots & \vdots \\[1em] \dfrac{\partial a}{\partial A_{1q}} & \dfrac{\partial a}{\partial A_{2q}} & \cdots & \dfrac{\partial a}{\partial A_{pq}} \end{bmatrix}, \text{(Numerator Layout)} \\ &= \begin{bmatrix} \text{Numerator Layout}\end{bmatrix}^T, \text{(Denominator Layout)} \end{align}\]

행렬 미분 종류 & Layout 총정리

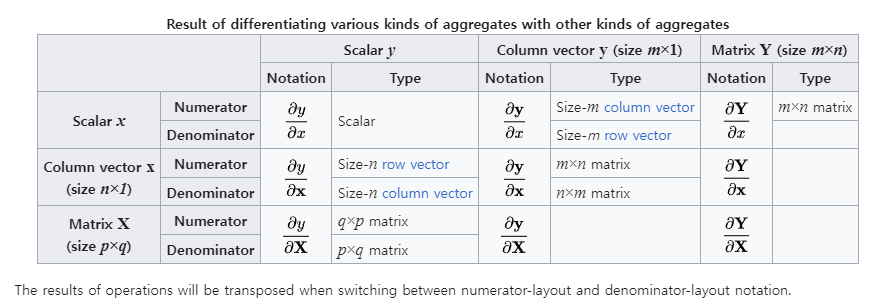참고 : Matrix calculus : Layout conventions

미분의 성질

벡터/벡터

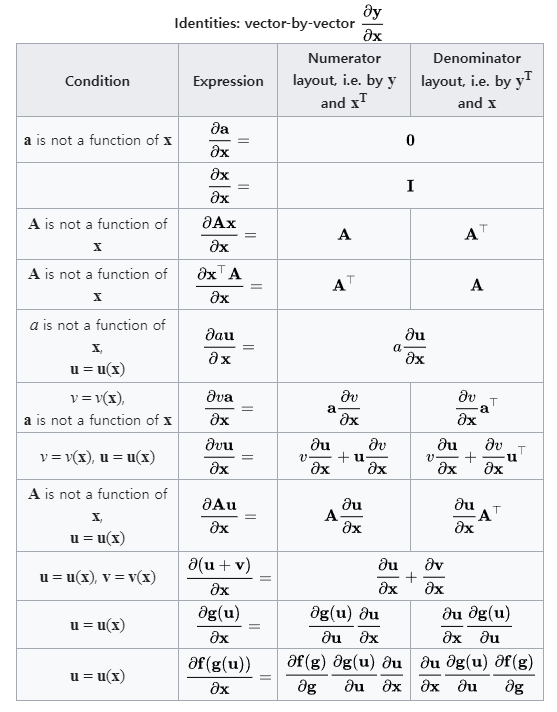참고 : Matrix calculus : Vector-by-bector identities

스칼라/벡터

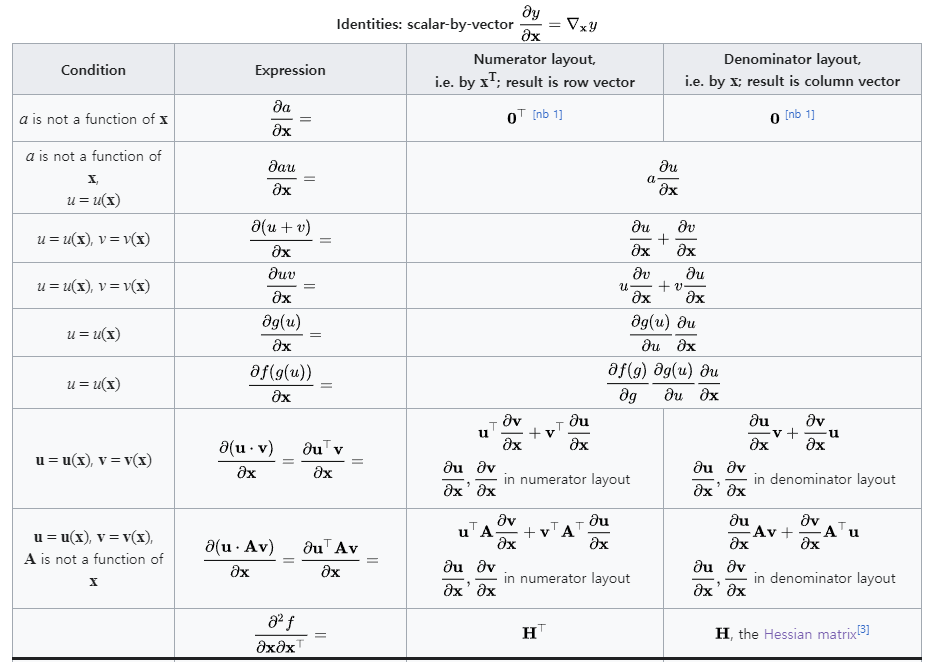
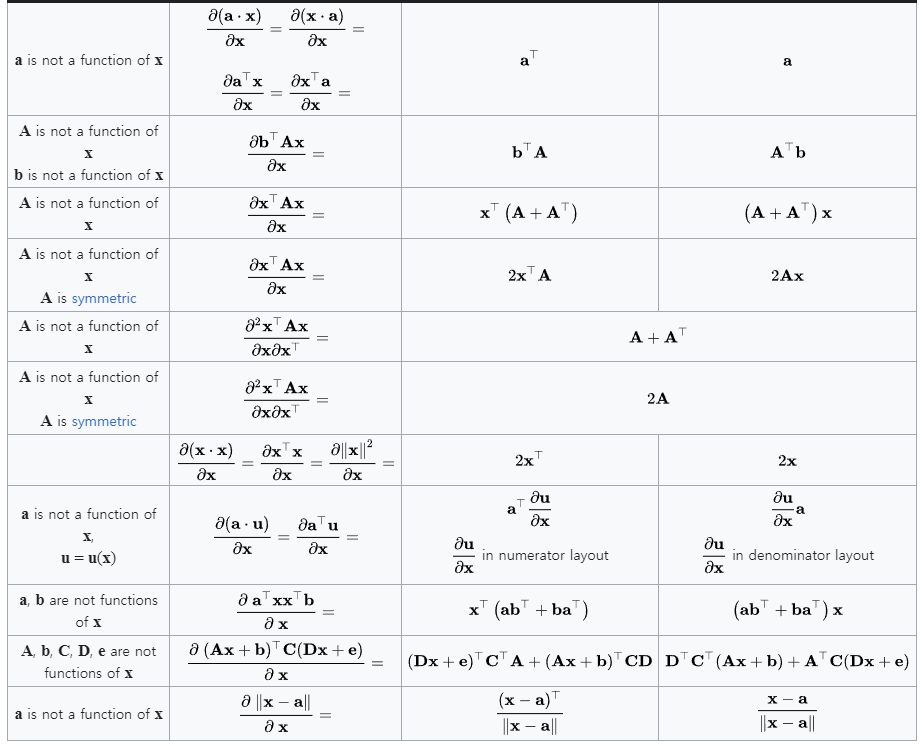참고 : Matrix calculus : Scalar-by-vector identities

양이 많아 보이지만, 요약하면 주요 법칙들은 몇개 안된다.

대표적으로 위의 벡터/벡터 미분의 성질표에서 아래 다섯가지 정도만 알아도 대부분의 문제를 해결할 수 있다.

$v = v(\mathbf{x})$,
$\mathbf{u},\mathbf{v} = \mathbf{u}(\mathbf{x}), v(\mathbf{x})$,
$\mathbf{A}$는 $\mathbf{x}$에 대한 행렬이 아님.
Numerator Layout,

\[\begin{align} \frac{\partial \mathbf{x}}{\partial \mathbf{x}} &= I,\text{(Identitiy)} \\[1em] \frac{\partial (\mathbf{u}+\mathbf{v})}{\partial \mathbf{x}} &= \frac{\partial \mathbf{u}}{\partial \mathbf{x}} + \frac{\partial \mathbf{v}}{\partial \mathbf{x}}, \text{(additive preserved)} \\[1em] \frac{\partial v \mathbf{u}}{\partial \mathbf{x}} &= v \frac{\partial \mathbf{u}}{\partial \mathbf{x}} + \mathbf{u} \frac{\partial v}{\partial \mathbf{x}}, \text{(scalar vector)} \\[1em] \frac{\partial \mathbf{A}\mathbf{u}}{\partial \mathbf{x}} &= A \frac {\partial \mathbf{u}}{\partial \mathbf{x}}, \text{(matrix vector)} \\[1em] \frac{\partial \mathbf{g}(\mathbf{u})}{\partial \mathbf{x}} &= \frac{\partial \mathbf{g}(\mathbf{u})}{\partial \mathbf{u}} \frac{\partial \mathbf{u}}{\partial \mathbf{x}}, \text{(chain rule)} \end{align}\]

스칼라/벡터 미분의 경우도 핵심적인 법칙은 아래와 같다.

\[\begin{align} \frac{\partial (u+v)}{\partial \mathbf{x}} &= \frac{\partial u}{\partial \mathbf{x}} + \frac{\partial v}{\partial \mathbf{x}} \\[1em] \frac{\partial uv}{\partial \mathbf{x}} &= u \frac{\partial v}{\partial \mathbf{x}} + v \frac{\partial u}{\partial \mathbf{x}} \\[1em] \frac{\partial u(g)}{\partial \mathbf{x}} &= \frac{\partial u(g)}{\partial g} \frac{\partial g}{\partial \mathbf{x}} \\[1em] \frac{\partial \mathbf{u}^T \mathbf{A} \mathbf{v}}{\partial \mathbf{x}} &= \mathbf{u}^T \mathbf{A} \frac{\partial \mathbf{v}}{\partial \mathbf{x}} + \mathbf{v}^T \mathbf{A} \frac{\partial \mathbf{u}}{\partial \mathbf{x}} \end{align}\]

나머지 내용들은 거의 다 위의 법칙들을 조합해서 나온 것들이다. 예를 들어 :

\[\begin{align} \frac{\partial \mathbf{a}^T \mathbf{x} \mathbf{x}^T \mathbf{b}}{\partial \mathbf{x}} &= \frac{\partial \mathbf{a}^T \mathbf{x}}{\partial \mathbf{x}} \cdot \left( \mathbf{x}^T \mathbf{b} \right) + \left( \mathbf{a}^T\mathbf{x} \right) \cdot \frac{\partial \mathbf{x}^T \mathbf{b}}{\partial \mathbf{x}} \nonumber \\[1em] &= \mathbf{a}^T \cdot \left( \mathbf{x}^T \mathbf{b} \right) + \left( \mathbf{a}^T\mathbf{x} \right) \cdot \mathbf{b}^T \nonumber \\[1em] &= \left(\mathbf{x}^T \mathbf{b}\right) \cdot \mathbf{a}^T + \left(\mathbf{x}^T \mathbf{a} \right) \cdot \mathbf{b}^T \nonumber \\[1em] &= \mathbf{x}^T \left( \mathbf{a}\mathbf{b}^T + \mathbf{b} \mathbf{a}^T\right) \\ \nonumber \\ \frac{\partial \lVert \mathbf{x} - \mathbf{a} \rVert}{\partial \mathbf{x}} &= \frac{\partial}{\partial \mathbf{x}}\left[ \left(\mathbf{x} - \mathbf{a} \right)^T\left( \mathbf{x} - \mathbf{a}\right) \right]^{1/2} \nonumber \\[1em] &= \frac{1}{2}\frac{1}{\sqrt{\left(\mathbf{x}-\mathbf{a}\right)^T\left(\mathbf{x}-\mathbf{a} \right)}} \frac{\partial}{\partial \mathbf{x}}\left[ (\mathbf{x} - \mathbf{a})^T (\mathbf{x} - \mathbf{a}) \right] \nonumber \\[1em] &= \frac{1}{2 \lVert\mathbf{x} -\mathbf{a} \rVert}\left( 2 (\mathbf{x} - \mathbf{a})^T \frac{\partial (\mathbf{x} - \mathbf{a})}{\partial \mathbf{x}} \right) \nonumber \\[1em] &= \frac{1}{2\lVert \mathbf{x} - \mathbf{a} \rVert}\left(2(\mathbf{x} - \mathbf{a})^T I \right) \nonumber \\[1em] &= \frac{(\mathbf{x} - \mathbf{a})^T}{\lVert \mathbf{x}-\mathbf{a}\rVert} \end{align}\]

등이 있다.