미분 가능한 다변수 함수의 극소값과 헤시안 행렬
미분 가능한 다변수 함수의 극값과, 극대 극소 판별에 대해 다룬다.
참고 1 : 모두를 위한 컨벡스 최적화
참고 2 : Maximum & Minimum
참고 3 : Hessian Matrix
어떤 함수의 극점(extremum point), 그 중에서도 특히 극소점(local minimum point)은 최적화 문제에서 아주 중요하다. 정의 자체에 의해서 함수의 극소점은 최적화 문제의 최적해(optimal solution)의 주요 후보가 되기 때문이다.
이 포스트에서는 일변수 함수의 극점을 찾는 내용을 먼저 다루고, 이를 다변수 함수로 확장하는 방법을 설명한다.
극대, 극소와 극값의 정의
극대, 극소는 함수의 최소값과 최대값에 관련된 개념이다.
기본적으로 최소와 최대를 말하려면 최소한 어떠한 구간(domain) $D$ 를 정해줘야 한다.
예를 들어, $y=x^2$ 함수를 살펴보자. 보통 이 함수의 최소값이 어디냐고 물어보면 $x=0$이라고 답할 것이다.
하지만 그것은 암묵적으로 $D = (- \infty, + \infty)$ 임을 깔고 들어가기 때문에 나온 답이다. $D = [1, \infty]$인 구간에서의 최소값을 찾으라고 하면 더 이상 $x=0$은 최소값이 아니게 된다. 따라서 최소값과 최대값이라는 것 자체가 항상 그것이 정의된 구간이 있어야 의미가 있다.
이때 구간에 따라 특이한 성질을 갖는 지점이 있다. 바로 극대와 극소이다.
고등학교 교과서에 나온 극대와 극소의 사전적인 정의는 다음과 같다 :
- 극대 : 주변의 값들보다 더 큰 값이 존재하는 지점
- 극소 : 주변의 값들보다 더 작은 값이 존재하는 지점
이를 좀 더 수학적으로 접근하면 다음과 같다.
함수 $f(x) : \mathbb{R} \rightarrow \mathbb{R}$에 대해서, 모든 작은 임의의 양수 $\delta$에 대해서 $x \in D, \lvert x- x^* \rvert < \delta$이면서 $f(x^* ) \geq f(x)$인 $x$가 존재하면, 그 $x$를 극소점(local minimum point) 이라 한다. 반대로 $f(x^* ) \leq f(x)$인 $x$가 존재하면, 그 $x$를 극대점(local maximum point) 이라 한다.
\[\begin{align} \forall \delta >0, \exists x\in D \quad s.t. \quad \lvert x - x^* \rvert < \delta ,f(x^*) \geq f(x) \Rightarrow x \text{ is local minimum point} \\ \forall \delta >0, \exists x\in D \quad s.t. \quad \lvert x - x^* \rvert < \delta ,f(x^*) \leq f(x) \Rightarrow x \text{ is local maximum point} \end{align}\]
위에 나온 함수 $y=x^2$를 다시 살펴보자.
이 함수는 $x=0$ 근처에서 모든 작은 임의의 양수 $\delta$만큼 떨어진 지점들, $\lvert 0 - x^* \rvert<\delta$ 에 대해 $y(x^*) \leq y(0)$을 만족한다. 이는 아무리 작은 $\delta$를 잡아도 만족한다. 이는, $x=0$ 주변에서 $y=x^2$의 값이 최소임을 의미한다. 따라서 $x=0$은 극소점이라고 볼 수 있다.
극소점과 극대점을 합쳐서 극점(extremum point) 이라 하며, 각각의 함수값을 극소값과 극대값이라 하고, 이를 합쳐서 극값(extremum value) 이라 한다.
일변수 함수
극점의 판별과 극대 극소, 변곡점의 구분
위의 정의에 의해, 미분가능하고 연속인 함수에 대해 언제나 극점의 기울기는 0일 수밖에 없다. 이는 미분의 정의에 의해, 극점에서의 접선의 기울기는 0이기 때문이다.
일반적으로 미분 가능한 일변수 함수에 대해 극점을 찾는 방법은 다음과 같다.
$f(x) : \mathbb{R} \rightarrow \mathbb{R}$에 대해 :
\[\begin{align} y'(x)=0, \begin{cases} y''(x) > 0 & \text{ : 극소(local minimum point)} \\ y''(x) < 0 & \text{ : 극대(local maximum point)} \\ y''(x) = 0 & \text{ : 변곡점(inflection point)} \end{cases} \end{align}\]
예시로 다음 함수가 있다.
$f(x) = x^3 + 3x^2 - 9x + 5 = (x-1)^2(x+5)$,
$f’(x) = 3x^2 + 6x - 9 = 3(x-1)(x+3)$,
$f’‘(x) = 6x + 6=6(x+1)$
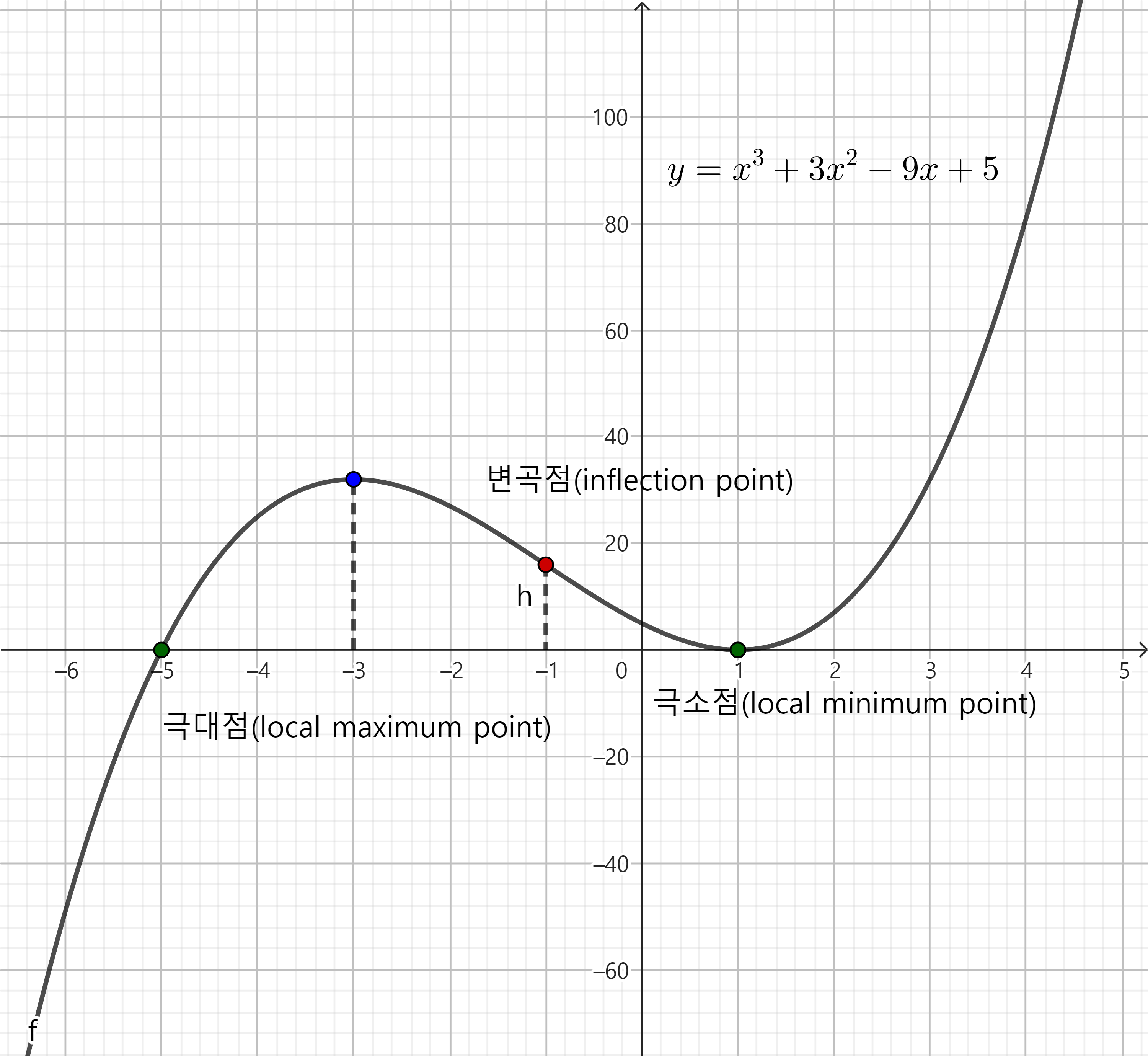$f(x) = x^3 + 3x^2 - 9x + 5$의 그래프
이때, 재미있는 점은, $f’‘$의 부호에 따라 함수가 볼록한 구간과 오목한 구간이 나뉘어 진다는 것이다.
이 아이디어는 미분가능한 다변수 함수의 헤시안 행렬(Hessian matrix)과, positive definite matrix, negative definite matrix의 개념으로 확장된다.
다변수 함수
다음과 같은 미분 가능한 다변수 함수를 생각해보자, $f : \mathbb{R}^n \rightarrow \mathbb{R}$. 그리고 n차원 실수 벡터, $x=\begin{bmatrix}x_1 & \cdots & x_n\end{bmatrix}^T \in \mathbb{R}^n$, 가 있다면, 그때의 다변수 함수의 함수값 역시 $f(x)$로 표기할 수 있다.
이 다변수 함수의 극점을 찾는 방법은 일변수 함수와 비슷하다.
\[\begin{align} \frac{\partial f}{\partial x} = 0, \begin{cases} \frac{\partial^2 f}{\partial x^2} \text{ : positive definite matrix} & \rightarrow \text{극소(local minimum point)} \\ \frac{\partial^2 f}{\partial x^2} \text{ : negative definite matrix} & \rightarrow \text{극대(local maximum point)} \\ \text{else : indefinite} & \rightarrow \text{말안장점(saddle point)} \end{cases} \end{align}\]
하나씩 짚어 보자
그라디언트 벡터(Gradient vector)
그라디언트 벡터(gradient vector)는 다변수 함수의 미분을 벡터로 표현한 것이다. 기존 일변수함수에서 미분은 스칼라였지만, 다변수 함수에서는 함수를 구성하는 각각의 변수에 대한 편미분들이 벡터로 표현된다.
일변수 함수에서의 1계도함수는 함수의 기울기를 나타냈는데, 이는 다르게 말하면 특정 지점에서 변수값을 증가시킬때, 함수값이 어떻게 변하는지에 대한 정보이다.
예를 들어, 일변수 함수 $f_1 = x^2+2$의 1계도 미분은 $f_1’ = 2x$이다. $f_1’(1) = 2 > 0$ 라는 뜻은, $x=1$에서 $x$값을 증가시키면 함수값이 2의 속도로 증가한다는 말과 비슷하다. 반대로 $f_1’(-1) = -2 < 0$ 라는 뜻은, $x=-1$에서 $x$값을 증가시키면 함수값은 2속도로 감소한다는 말이 된다.
이를 다변수 함수로 확장한 개념이 그라디언트 벡터(Gradient vector)이며, 이는 특정 지점에서 변수값을 증가시킬 때, 함수값이 어디로 변하는지에 대한 방향과 크기를 나타낸다.
다변수 함수의 그라디언트 벡터는 다음과 같이 표기한다 :
\[\begin{align} \nabla f(x) = \begin{bmatrix} \dfrac{\partial f}{\partial x_1} \\ \vdots \\ \dfrac{\partial f}{\partial x_n} \end{bmatrix} = \left(\frac{\partial f(x)}{\partial x}\right)^T \end{align}\]행렬 미분의 표기법에 대해선 행렬 미분 포스트 참고
예를 들어 다음의 벡터와 함수, $x = \begin{bmatrix}a & b\end{bmatrix}^T \in \mathbb{R}^2, f_2(x) = a^2 + b^2 + 2$에 대하여,
그라디언트 벡터는 다음과 같다 :
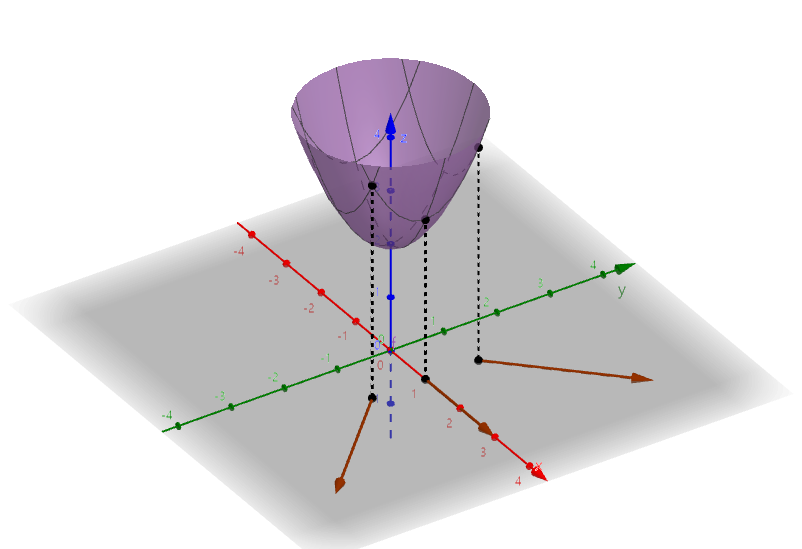
다양한 지점에서의 그라디언트 벡터를 그려보면, 해당 방향에서 값이 증가하는 벡터를 나타냄을 알 수 있다.
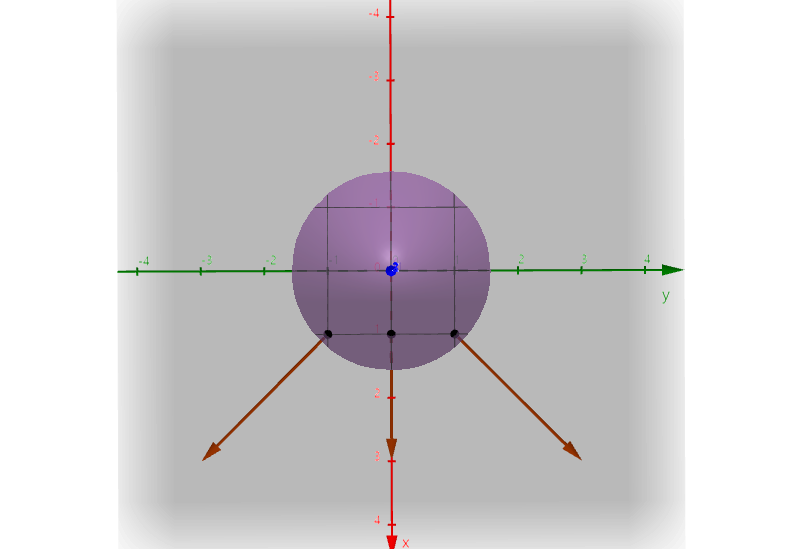위에서 내려다본 $f=x^2 + y^2 + 2$의 그래프와 그라디언트 벡터
3D 뷰
이때, $\nabla f = 0$이 되는 지점은 일변수 함수때와 마찬가지로 극점의 후보가 될 수 있다.
이제 이 지점이 극소점인지, 극대점인지, 말안장점인지 판별하기 위해서는, 헤시안 행렬(Hessian matrix)을 사용한다.
헤시안 행렬(Hessian matrix)
헤시안 행렬은 미분 가능한 다변수 함수의 2차 편미분의 행렬 형태이며, 다음과 같이 정의된다 :
\[\begin{align} H(f) = \begin{bmatrix} \dfrac{\partial^2 f}{\partial x_1^2} & \dfrac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \dfrac{\partial^2 f}{\partial x_1 \partial x_n} \\[1em] \dfrac{\partial^2 f}{\partial x_2 \partial x_1} & \dfrac{\partial^2 f}{\partial x_2^2} & \cdots & \dfrac{\partial^2 f}{\partial x_2 \partial x_n} \\[1em] \vdots & \vdots & \ddots & \vdots \\[1em] \dfrac{\partial^2 f}{\partial x_n \partial x_1} & \dfrac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \dfrac{\partial^2 f}{\partial x_n^2} \end{bmatrix} \end{align}\]보통 이를 처음 연구하고 발표한 수학자 헤세(Ludwig Otto Hesse)의 앞글자를 따서 $H$로 표기한다.
앞선 예시의 헤시안 행렬은 다음과 같다 :
\[\begin{align} H(f_2) = \begin{bmatrix} \dfrac{\partial^2 f_2}{\partial a^2} & \dfrac{\partial^2 f_2}{\partial a \partial b} \\[1em] \dfrac{\partial^2 f_2}{\partial b \partial a} & \dfrac{\partial^2 f_2}{\partial b^2} \end{bmatrix} = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \end{align}\]대단히 유용한 성질들이 많다.
해당 지점에서의 함수의 곡률을 나타낼 수도 있고, positive definite, negative definite인지를 통해 이 지점이 볼록한지 오목한지 판정하는데도 사용된다. 또한 테일러 급수를 다변수함수로 확장할 때에도 사용된다.
만약 2차 편미분에 대해서 연속이라면, 헤시안 행렬은 대칭 행렬이 된다($H = H^T$)
일변수 함수의 2계도함수와 비슷한 개념이며, 다변수 함수로의 확장판이다. 이때, 기존의 극점 판별에 사용했던 2계도 함수의 극값 판별법을 역시도 다변수 함수로 확장 가능하며, 여기서 positive definite matrix, negative definite matrix의 개념이 사용된다.
헤시안 행렬은 해당 지점에서의 곡률에 대한 정보를 나타내는데, 이게 positive definite matrix라는 뜻은 해당 지점에서의 모든 방향으로의 곡률이 양수임을 의미한다.
즉, 해당 지점에서 모든 방향으로 함수가 아래로 볼록하게 구부러져 있음을 나타내므로 이는 극소점(local minimum point)이 된다.
반대로 negative definite matrix이면 해당 지점에서의 모든 방향으로의 곡률이 음수임을 의미한다. 즉, 해당 지점에서 모든 방향으로 함수가 위로 오목하게 구부러져 있으므로 이는 극대점(local maximum point)을 의미한다.
indefinite이라면, 일변수함수에서의 변곡점과 같은 구조가 되는데, 보통 말안장점(saddle point)라 한다. 마치 말안장 처럼 생겨서 그런 이름이 붙었다.
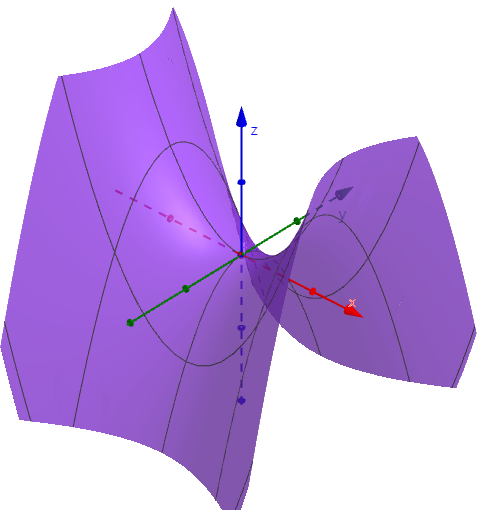
대표적으로 $f(x,y) = x^2 - y^2$의 그래프를 살펴보면 :
이렇게 생긴 그래프이다
$f=x^2-y^2$의 그래프
진짜로 말안장을 닮아서 saddle point라고 불린다
Positive definite matrix, Negative definite matrix
Positive definite matrix인지, Negative definite matrix는 정방행렬에 대해서만 정의되며, 다음과 같다 :
\[\begin{align} \text{Positive definite matrix} & : \text{모든 벡터 } x \neq 0 \text{에 대해 } x^T H x > 0 \\ \text{Negative definite matrix} & : \text{모든 벡터 } x \neq 0 \text{에 대해 } x^T H x < 0 \end{align}\]
저게 Positive, Negative와 무슨 상관인지 모르겠다면, 다음과 같은 예시를 생각해볼 수 있다.
어떤 실수 스칼라 $a$ 에 대해서 이 스칼라가 양수인지, 음수인지 판별하는 방법을 이렇게도 생각해 볼 수 있다.
\[\begin{align} \text{Positive} & : \text{모든 실수 } x \neq 0 \text{에 대해 } ax^2 > 0 \\ \text{Negative} & : \text{모든 실수 } x \neq 0 \text{에 대해 } ax^2 < 0 \end{align}\]$x^2 > 0$ 이기 때문에, $a$가 양수이면 $ax^2$도 양수가 되고, 음수이면 $ax^2$도 음수가 된다.
이를 행렬로 확장한다면, 행렬 $H$가 Positive definite matrix이기 위해서는, 모든 벡터 $x \neq 0$에 대해 $x^T H x > 0$이어야 하며, Negative 버전은 반대로 될 것이다.
똑같이 $x^Tx = \lVert x \rVert^2 >0$ 이기 때문에, $H$가 Positive definite matrix이면, $x^T H x$도 양수가 되고, Negative 버전은 음수가 된다.
다른 이해 방식은 다변수함수의 2차항의 부호로 생각하는 방법도 있다. 예를 들어 $f(a,b,c) = 2a^2 + 5b^2 + c^2 -4ab - 2bc$는,$(a,b,c) \neq 0$이면 $f > 0$을 만족하는데, 이를 완전제곱식의 합과, 행렬로 동시에 표현하면 다음과 같다 :
\[\begin{align} f(a,b,c) &= 2a^2 + 5b^2 + c^2 -4ab - 2bc \nonumber \\ &= a^2 + (a-2b)^2 + (b-c)^2 >0 \nonumber \\ &= \begin{bmatrix}a & b & c\end{bmatrix} \begin{bmatrix}2a-2b \\ -2a+5b-c \nonumber \\ -b+c\end{bmatrix} \nonumber \\ &= \begin{bmatrix}a & b & c\end{bmatrix} \begin{bmatrix}2 & -2 & 0 \\ -2 & 5 & -1 \\ 0 & -1 & 1\end{bmatrix} \begin{bmatrix}a \\ b \\ c\end{bmatrix} \nonumber \\ & = x^T H x > 0, x = \begin{bmatrix}a & b & c\end{bmatrix}^T \\ \nonumber \\ & \therefore H \text{ : Positive definite matrix} \nonumber \end{align}\]Positive definite matrix이면서, 동시에 0도 될 수 있는 matrix를 Positive semidefinite matrix라고 한다.
반대는 Negative semidefinite matrix이다.
선행 주 소행렬식(leading principal minors)
대칭행렬 $A \in \mathbb{R}^{n \times n}, A^T=A$에 대해서, 선행 주 소행렬식(leading principal minors)를 체크하면 Positive definite matrix인지, Negative definite matrix인지 판별할 수 있다.
$A$의 leading principal minors는 $A$의 첫 $k$개의 행과 열을 선택하여 만든 $k \times k$ 부분행렬의 행렬식들을 말한다.
예를 들어, $\begin{bmatrix}a & b \ c & d\end{bmatrix}$의 leading principal minors는 $\lvert \begin{bmatrix} a\end{bmatrix} \rvert$,$\left\lvert \begin{bmatrix} a & b \ c & d\end{bmatrix} \right\rvert$로 2개다.
이때, 정방행렬 $A$가 Positive definite matrix이기 위해서는, $A$의 모든 leading principal minors가 양수이어야 한다. $k$ 번째 principal minor를 $D_k$라고 했을 때 다음과 같이 표현할 수 있다 :
\[\begin{align} D_1 &> 0, D_2 > 0, \cdots, D_n > 0 \nonumber \\ \end{align}\]반대로, Negative definite matrix이기 위해서는, $A$의 leading principal minors가 번갈아가며 음수, 양수가 되어야 한다 :
\[\begin{align} D_1 < 0, D_2 > 0, D_3 < 0, \cdots, (-1)^n D_n > 0 \nonumber \\ \end{align}\]이를 그림으로 표현하면 다음과 같다
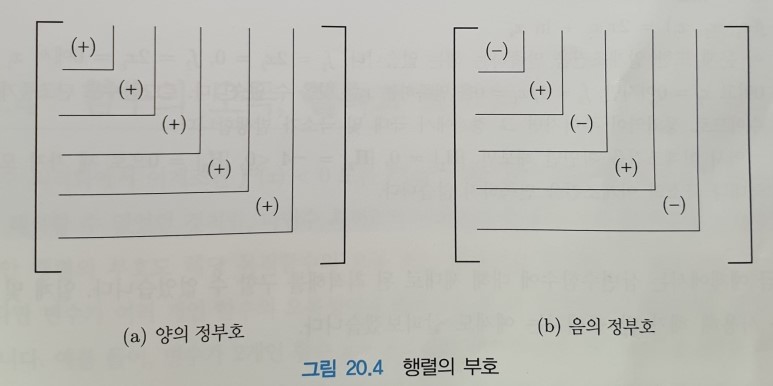출처 : https://blog.naver.com/modernyoon/221578605613
이도저도 아니면 indefinite 행렬이다.
Convex function과의 관계
2번 미분 가능하고 연속인 Convex 함수에 대해서, 전 구간에서의 헤시안 행렬이 positive semidefinite 임이 증명되어 있다.
반대로 전 구간에서의 헤시안 행렬이 positive semidefinite 이면, 해당 함수는 Convex 함수이다.