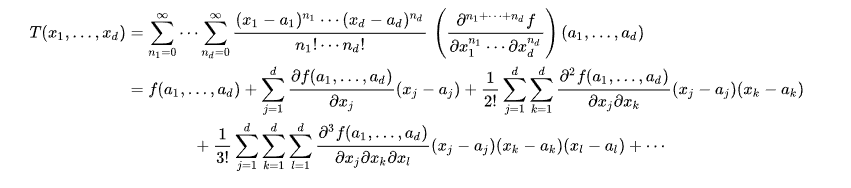다변수 함수의 테일러 근사와 tangent hyperplane

참고 : Taylor Series

다변수 함수의 테일러 확장은 어떻게 정의되고 왜 필요한지 살펴보자.

테일러 급수

역사

급수에 대한 고민은 고대 그리스 때부터 이어졌다. 제논의 역설(Zeno’s paradox)은 무한급수의 개념을 포함하고 있었으며, 이후에도 다양한 수학자들이 급수에 대한 연구를 이어왔다.

14세기의 인도 수학자 Madhava of Sangamagrama가 몇몇 삼각함수의 급수를 유도한 것으로 추정되며, 17세기 후반에 뉴턴도 몇몇 삼각 함수의 테일러 급수를 유도했다.

그러다가 18세기 영국 수학자 브루어노이 테일러(Brook Taylor)가 테일러 급수를 처음 소개하며 이름을 붙였고, 드디어 테일러 급수(Taylor Series)라는 이름이 생기게 된다. 18세기 중반에 콜린 매클로린(Collin Maclaurin)이 테일러 급수의 특수한 경우에 출판하여 매클로린 급수(Maclaurin Series)라는 이름이 붙게 된다.

정의

테일러 급수, 또는 테일러 확장(expansion)은 다음과 같이 정의된다

테일러 급수(Taylor Series)
실수 또는 복소수에 대한 함수 $f(x)$가 $a$에서 무한히 미분 가능할 때, 다음과 같은 멱급수이다. \(\begin{align} f(x) &= f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + \cdots \nonumber \\ &= \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n \end{align}\)

이때, $a=0$인 경우의 테일러 급수를 특별히 매클로린 급수(Maclaurin series)라고 부른다.

매클로린 급수(Maclaurin Series) \(\begin{align} f(x) &= f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \cdots + \frac{f^{(n)}(0)}{n!}x^n + \cdots \nonumber \\ &= \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!}x^n \end{align}\)

이는 무한히 미분 가능한 함수이기만 하면 어떤 함수든 테일러 급수로 표현할 수 있었기에, 다양한 함수들의 정의역을 확장하는 데에도 사용되었다.
대표적으로 $e^x$ 함수의 정의역을 복소수로 확장한 $e^{i\theta} = \cos{\theta} + i\sin{\theta}$는 테일러 급수를 통해 확장될 수 있으며, 이는 오일러 공식(Euler’s formula) 으로도 알려져 있다.

예시

테일러 급수도 엄연히 수렴 반경이 존재한다. 수렴 반경을 벗어난 범위에 대해서는 테일러 급수는 수렴하지 않으므로 본래의 함수와 다른 값을 가질 수 있다.

다음은 자주 사용되는 삼각함수와, exponential 함수의 테일러 급수 형태이다.

\[\begin{align} e^x &= 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots \nonumber \\ &= \sum_{n=0}^{\infty} \frac{x^n}{n!}, \quad \text{for all } x \in \mathbb{R} \\ \sin{x} &= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots \nonumber \\ &= \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n+1}}{(2n+1)!}, \quad \text{for all } x \in \mathbb{R} \\ \cos{x} &= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots \nonumber \\ &= \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n}}{(2n)!}, \quad \text{for all } x \in \mathbb{R} \end{align}\]

1차 테일러 근사

테일러 급수는 고차항을 계속 추가할 수록 원 함수와 동일해진다. 이를 이용해서 특정 차수의 항까지만 고려한 근사식을 만들 수 있다. 이를 테일러 근사(Taylor approximation)이라고 한다.

그 중에서도 1차항 까지만 고려한 근사식을 1차 테일러 근사라고 하며, 다음과 같다 : \(f(x) \approx f(a) + f'(a)(x-a)\)

재미있게도, 이는 함수 $f(x)$ 위의 점, $(a,f(a))$에서 접선의 방정식 또는 접선(tangent line)과 완전히 동일하다. 그래서 1차 테일러 근사는 선형 근사(linear approximation)이라고도 불린다.

이때 $f:\mathbb{R}^2\rightarrow \mathbb{R}$ 가 되면 3차원 공간에서의 접평면(tangent plane)이 되고. 그 이상의 고차원 함수에 대해서는 tangent hyperplane의 개념으로 확장되게 된다.
여기부턴 다변수 함수의 영역이 된다.

다변수 함수의 테일러 확장

정의

다변수 함수로의 테일러 확장은 다음과 같이 정의된다 :

다변수 함수의 테일러 확장
다변수 함수 $f(x_1, x_2, \ldots, x_n)$가 $a_1, a_2, \ldots, a_n$에서 무한히 미분 가능할 때, 다음과 같은 테일러 급수로 확장할 수 있다. \(\begin{align} f(x_1, x_2, \ldots, x_n) &= f(a_1, a_2, \ldots, a_n) + \sum_{i=1}^{n} \frac{\partial f}{\partial x_i}(a_1, a_2, \ldots, a_n)(x_i - a_i) \nonumber \\ &+ \frac{1}{2!} \sum_{i=1}^{n} \sum_{j=1}^{n} \frac{\partial^2 f}{\partial x_i \partial x_j}(a_1, a_2, \ldots, a_n)(x_i - a_i)(x_j - a_j) + \cdots \nonumber \\ &+ \frac{1}{n!} \sum_{i_1=1}^{n} \cdots \sum_{i_n=1}^{n} \frac{\partial^n f}{\partial x_{i_1} \cdots \partial x_{i_n}}(a_1, a_2, \ldots, a_n)(x_{i_1} - a_{i_1}) \cdots (x_{i_n} - a_{i_n}) + \cdots \end{align}\)

물론 $a_1 = a_2 = \cdots = a_n = 0$인 경우의 테일러 확장도 특별히 매클로린 확장(Maclaurin expansion)이라고 부른다.

다변수 테일러 급수의 고차항은 계산하기엔 너무 많은 비용이 들면서, 근사 효과는 저차항에 비해 미비하다. 따라서 종종 1~2차 항 까지만 사용하여 비선형 함수를 선형 또는 2차 형식으로 근사하는 것이 일반적이다.

1차 테일러 근사

위 식에서 1차식 까지만을 자르면, 1차 테일러 근사는 다음과 같다 :

1차 테일러 근사
\(f(x_1, x_2, \ldots, x_n) \approx f(a_1, a_2, \ldots, a_n) + \sum_{i=1}^{n} \frac{\partial f}{\partial x_i}(a_1, a_2, \ldots, a_n)(x_i - a_i)\)

이를 행렬 미분의 형태, 또는 gradient vector로 표현하면 다음과 같다 :

\[f(x) \approx f(a) + \nabla f(a)^T(x-a)\]

재미있게도, 1차 테일러 근사가 나타내는 것은 함수 $f(x)$ 위의 점, $(a,f(a))$에서의 접평면(tangent hyperplane)이다.

벡터 $x \in \mathbb{R}^n$과 함수 $f:\mathbb{R}^n \rightarrow \mathbb{R}$에 대해, 함수 $F(x,k) = f(x) - k : \mathbb{R}^{n+1} \rightarrow \mathbb{R}$ 를 생각하자. 이때 $k = f(x)$라면, $F(x,k) = 0$이 된다.

이제 $F(x,k)=0$을 만족하는 고차원 곡면 위의 점 $(x_0,k_0)$에서의 접평면을 생각해보자. $F(x(t),k(t)) = 0$을 만족하며 매개변수 $t$를 가지고 각 변수들이 움직일 때, $F$를 전미분 하여 다음이 반드시 성립함을 알 수 있다 :

\[\begin{align} \frac{d F}{d t} &= \begin{bmatrix} \dfrac{\partial F}{\partial x_1} & \cdots \dfrac{\partial F}{\partial x_n} & \dfrac{\partial F}{\partial k}\end{bmatrix} \begin{bmatrix} \dfrac{dx_1}{dt} \\ \vdots \\ \dfrac{dx_n}{dt} \\[1em] \dfrac{dk}{dt} \end{bmatrix} = 0 \\ &= \nabla F(x)^T \begin{bmatrix} \dfrac{dx_1}{dt} \\ \vdots \\ \dfrac{dx_n}{dt} \\[1em] \dfrac{\partial k}{\partial t}\end{bmatrix}= 0 \end{align}\]

이는 어떠한 방식으로 곡면 위의 점에 접근하더라도, 해당 지점에서의 방향 벡터와 $\nabla F$ 가 언제나 수직함을 나타낸다. 따라서 해당 지점에서의 접평면의 법선 벡터(normal vector) $\vec{n}$은 $\nabla F$와 평행하다.

다음으로 평면의 정의에 따라, 특정 점 $(x_0,k_0)$을 지나고, 법선 벡터가 $\nabla F$인 평면은 다음과 같다 :

\[\begin{align} \begin{bmatrix} (x - x_0)^T & k - k_0 \end{bmatrix} \nabla F &= 0 \\ \begin{bmatrix} (x - x_0)^T & k - k_0 \end{bmatrix} \begin{bmatrix}\nabla f \\ -1 \end{bmatrix} &= 0 \nonumber \\ \begin{bmatrix} x - x_0 \end{bmatrix}^T\nabla f - k + k_0 =& 0 \nonumber \\ \nabla f^T(x - x_0) + k_0 =& k \nonumber \\ \nonumber \\ \rightarrow f(x) = f(x_0) + \nabla f^T(x - x_0) \end{align}\]

이는 $f(x)$의 다변수 1차 테일러 근사 (또는 선형 근사)와 완전히 동일하다.

2차 테일러 근사

위 식에서 2차항에서 자르면, 2차 테일러 근사가 되며 다음과 같다 :

2차 테일러 근사

\[\begin{align}f(x_1, x_2, \ldots, x_n) &\approx f(a_1, a_2, \ldots, a_n) \\ &+ \sum_{i=1}^{n} \frac{\partial f}{\partial x_i}(a_1, a_2, \ldots, a_n)(x_i - a_i) \\ &+ \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \frac{\partial^2 f}{\partial x_i \partial x_j}(a_1, a_2, \ldots, a_n)(x_i - a_i)(x_j - a_j)\end{align}\]

이를 행렬 미분의 형태로 표현하면 다음과 같다 :

\[f(x) \approx f(a) + \nabla f(a)^T(x-a) + \frac{1}{2} (x-a)^T H_f(a)(x-a)\]

이때 $H_f$는 헤시안 행렬(Hessian matrix)로 다음과 같이 정의된다 :

\[H_f = \begin{bmatrix} \dfrac{\partial^2 f}{\partial x_1^2} & \dfrac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \dfrac{\partial^2 f}{\partial x_1 \partial x_n} \\[1em] \dfrac{\partial^2 f}{\partial x_2 \partial x_1} & \dfrac{\partial^2 f}{\partial x_2^2} & \cdots & \dfrac{\partial^2 f}{\partial x_2 \partial x_n} \\[1em] \vdots & \vdots & \ddots & \vdots \\[1em] \dfrac{\partial^2 f}{\partial x_n \partial x_1} & \dfrac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \dfrac{\partial^2 f}{\partial x_n^2} \end{bmatrix} = \nabla^2f\]

2차 테일러 근사는 해당 지점에서의 변화율과 곡률을 동시에 고려한 곡면을 나타낸다.

최적화 분야에서는 2차 테일러 근사를 주로 사용하는데, 1차 선형 근사는 평면의 형태여서 min max가 존재하지 않지만, 2차 테일러 근사는 곡면의 형태이므로 min max가 존재할 수 있다는 점이 크다.

특히, 2차식 형태를 가진 convex함수의 극소점을 찾는 것은 closed form으로 정리되므로 월등하게 빠른 수렴 속도를 확보할 수 있다.

나중에 소개할 Gradient Descent와 Newton Method가 각각 1차 테일러 근사와 2차 테일러 근사를 이용한 최적화 알고리즘이다.