뉴턴 메소드(Newton's method)

경사 하강법보다 일반적으로 더 빠른 수렴속도를 가진 Newton’s method 에 대해 알아본다.

참고 1 : Newton’s method in optimization
참고 2 : 모두를 위한 컨벡스 최적화, Newton’s method
참고 3 : CMU-convex optimiazation, Newton method

Newton’s method

테일러 2차 근사에서, Hessian matrix를 단위행렬로 근사했던 경사하강법과 달리, 완전한 테일러 2차 근사식의 최소값을 찾으며 해에 접근하는 방법이다.
해의 근처에서 quadratic convergence 특성을 보이며, 일반적으로 경사하강법(gradient descent)보다 빠르다.
대신 계산량과 필요한 메모리가 경사하강법보다 많고, 수치 에러(numerical error)에 더 민감하다는 단점도 있다.

2번 미분 가능한 convex 함수, $f: \mathbb{R}^n \rightarrow \mathbb{R}$, 벡터 $x\in \mathbb{R}^n$가 있다. $f(x)$를 최소화하는 문제를 풀 때, Newton’s method는 다음과 같이 반복적으로 업데이트한다.

Newton’s method

\[\begin{align} x^{(0)} & \in \mathbb{R}^n, \nonumber \\ x^{(k+1)} &= x^{(k)}-H(x^{(k)})^{-1} \nabla f(x^{(k)}) \\ \nabla^2 f &= H : \text{Hessian matrix} \end{align}\]

유도 및 해석

2nd taylor expansion 유도

경사하강법 포스트 에서 경사하강법을 유도했던 것처럼, Newton’s method도 유도해보자.

Newton’s method는 2차 테일러 근사의 Hessian matrix, $H$를 별도의 행렬로 대체하지 않고 있는 그대로를 사용한다.

임의의 점 $a$에서 2차 테일러 근사를 전개하면 :

\[\begin{align} f(x) &\approx f(a) + \nabla f(a)^T(x-a) + \frac{1}{2}(x-a)^T H(a)(x-a) \nonumber \\ &= \hat{f}(x) \end{align}\]

이제, 2차 테일러 근사된 함수 $\hat{f}(x)$를 최소화 시키는 $x$ 를 찾아보자. 2계 미분 가능하고, 연속인 함수에 대해서 Hessian matrix는 대칭 행렬임을 기억하자 ($H = H^T$).

\[\begin{align} \frac{\partial \hat f(x)}{\partial x} &= \frac{\partial f(a)}{\partial x} + \frac{\partial }{\partial x}\left( \nabla f(a)^T (x-a) \right) + \frac{\partial }{\partial x}\left( \frac{1}{2}(x-a)^T H(a) (x-a) \right) \nonumber \\ &= 0 + \nabla f(a)^T+ \frac{1}{2}\left[ (x-a)^T H(a) + (x-a)^T H(a)^T \right] \nonumber \\ &= \nabla f(a)^T + (x-a)^T H(a), H = H^T \nonumber \\ \Rightarrow \left( \frac{\partial \hat{f}}{\partial x} \right)^T &= \nabla \hat{f} = \nabla f(a) + H(a)(x-a) = 0 \\ \nonumber \\ \therefore x &= a - H(a)^{-1}\nabla f(a) \\ \Rightarrow x^{(k+1)} &= x^{(k)} - H(x^{(k)})^{-1} \nabla f(x^{(k)}) \\ \end{align}\]

이는 위의 Newton’s method의 업데이트 식과 동일하다.
유도 과정을 통해 알 수 있듯이, 경사하강법 보다 뉴턴법이 더 온전한 테일러 근사를 사용하기 때문에 성능이 좋을 것임을 짐작할 수 있다.

예시로, $f(x_1, x_2) = (10x^2_1 + x^2_2)/2 + 5 \log{(1+e^{-x_1-x_2})}$ 에 대해서, 경사하강법과 뉴턴법을 비교해보자.
Newton method의 매 step 만큼 gradient descent 의 step을 진행한다고 했을 때, 다음과 같이 수렴한다

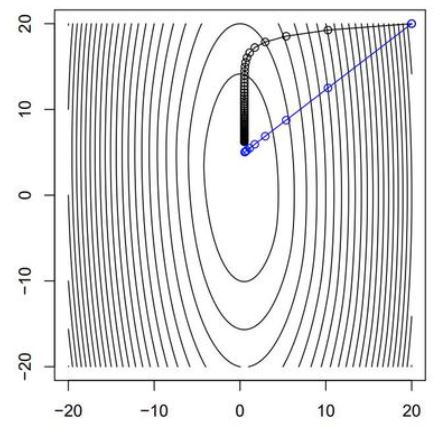검정이 Gradient descent, 파랑이 Newton’s method로 접근한 것이다. 출처

확실히 gradient descent 방법이 더 많은 iteration을 돌아야 수렴함을 알 수 있다.

Root finding 해석

기존의 newton method는 root-finding 분야에서는 조금 다른 내용이다.

참고 : Newton method, root finding

root finding은 어떤 방정식의 근을 찾는 분야이다. 일변수 함수, $f : \mathbb{R} \rightarrow \mathbb{R}$에 대해서 다음과 같다.

\[\begin{align} x_{x+1} = x_{k}-\frac{f(x_{k})}{f'(x_k)} \end{align}\]

이는 점 $(x_k, f(x_k))$에서 접선을 그린 후, 그 접선이 $x$ 축과 만나는 점을 $x_{k+1}$로 삼는 것과 동일하다.

\[\begin{align} y &= f'(x_{k})(x - x_{k}) + f(x_k), \text{tangent line at }(a, f(a)) \nonumber \\ 0 &= f'(x_{k})(x_{k+1} - x_{k}) + f(x_k) \nonumber \\ x_{k+1} &= x_{k} - \frac{f(x_k)}{f'(x_k)} \end{align}\]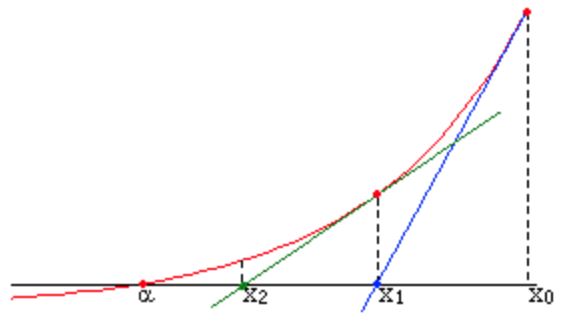

Newton’s method in 1D. 출처

이 root-finding이라는 부분은, 우리가 앞서 optimization에서 자주 사용했던 $\nabla f=0$을 구하는 부분과 비슷하다.

따라서, 이 newton method를 $\nabla f$의 root finding 문제에 적용해보자.

일변수 함수에서 tangent line으로 만들었으니, 이번엔 다변수 함수의 tangent hyperplane으로 확장해보자.
다변수 함수의 테일러 근사 포스트에서 다변수 함수의 테일러 선형 근사는 다음과 같다 :

\[\begin{align} f(x) &\approx f(a) + \nabla f(a)^T(x-a) \nonumber \\ \end{align}\]

이 경우엔, $\nabla f$에 대한 root를 찾는 문제이므로, 다음과 같이 바뀐다

\[\begin{align} \nabla f(x) &= \begin{bmatrix} f_1(x) \\ f_2(x) \\ \vdots \\ f_n(x) \end{bmatrix} \\ \therefore 0 &= \begin{bmatrix} f_1(a) + \nabla f_1(a)^T(x-a) \\ f_2(a) + \nabla f_1(a)^T(x-a) \\ \vdots \\ f_n(a) + \nabla f_1(a)^T(x-a) \\ \end{bmatrix} \nonumber \\ &= \begin{bmatrix}f_1(a) \\ f_2(a) \\ \vdots \\ f_n(a)\end{bmatrix} + \begin{bmatrix}\nabla f_1(a)^T \\ \nabla f_2(a)^T \\ \vdots \\ \nabla f_n(a)^T\end{bmatrix}(x-a) \nonumber \\ &= \nabla f(a) + \nabla^2 f(a)(x-a) \\ \Rightarrow & x = a - \nabla^2 f(a)^{-1} \nabla f(a) \nonumber \\ \Rightarrow & x^{(k+1)} = x^{(k)} - \nabla^2 f(x^{(k)})^{-1} \nabla f(x^{(k)}) \end{align}\]

이는 optimizaiton 에서의 Newton method와 동일한 식이 된다.

성질

Affine invariance

뉴턴 메소드의 주요한 성질 중 하나는, affine 변환에 대해 독립적이라는 것이다. 즉, optimization이 이뤄지는 좌표계가 affine 변환이 되어도 수렴 절차에 아무런 변화가 없다.

반대로 gradient descent 방법은 affine 변환에 상관이 있어서 좌표계의 구조에 따라 수렴 속도가 달라지기도 한다.

2번 미분 가능한 함수 $f: \mathbb{R}^n \rightarrow \mathbb{R}$와 nonsingular 행렬 $A \in \mathbb{R}^{n \times n}$ 에 대해 함수 $g(y) = f(Ay)$를 만들어서 적용해도 동일한 수렴성을 보인다는 뜻이다.

증명 과정은 참고 : 모두를 위한 컨벡스 최적화, Newton’s method

Local convergence analysis

뉴턴 메소드의 두번째 성질은, 특정 조건을 만족할 시 해로 수렴함이 보장된다는 것이다. 이를 local convergence 라 한다.

그 조건은 다음과 같다.

1. $f$가 convex function
2. $f$가 두번 미분 가능
3. $\nabla f$는 $L$에 대해서 Lipschitz continuous
4. $f$는 파라미터 $m$에 대해서 strong convex
5. $\nabla^2f$가 $M$에 대해서 Lipschitz continuous

위 조건을 전부 만족하면, pure phase 수렴 과정에서 quadratic convergence가 이루어진다.

\[\begin{align} \lVert \nabla f(x^+) \rVert_2 \leq \frac{M}{2m^2} \lVert \nabla f(x) \rVert_2^2 \end{align}\]

증명 과정은 참고 : 모두를 위한 컨벡스 최적화, Newton’s method

Damped Newton’s method

지금까지 유도한 pure newton method는 수렴성이 보장되지 않는다. 이때 경사하강법 포스트 에서 step size 선택 전략으로 사용했던 backtracking line search 를 적용하면, local convergence를 보장할 수 있다.
그렇게 약간 수정된 newton method를 damped newton’s method라 하며 다음과 같다 :

Damped Newton’s method

1. $0<\alpha < 1/2$, $0 < \beta < 1$, $0 로 정한다
2. step size, $t$의 초기값을 $t=t_0$
3. $f(x+tv) > f(x) + \alpha t \nabla f(x)^T v$ 인지 체크한다
4. 부등식이 성립한다면 $t$를 $t=\beta t$로 줄이고 다시 3번으로 돌아간다.
5. 부등식이 성립하지 않는다면 중단한다.

Quasi-Newton’s method

뉴턴 메소드는 Hessian matrix를 계산해야 하기 때문에 계산량이 많다는 단점이 있다. 이를 극복하기 위해, Hessian matrix를 근사하는 방법이 있는데, 이를 Quasi-Newton’s method라 한다.

즉, $\nabla^2f$를 직접 계산하지 않고, 매번 positive definite 인 대칭 행렬 $H$로 근사하며 업데이트를 해 나가는 방식이다.

참고 : Quasi-Newton method

보통 다음과 같은 특징을 가진다

• Hessian matrix를 직접 구하지 않고, 매 스텝마다 업데이트 해서 유지한다. 최소한의 계산 비용으로 $H^{-1}$을 구하는 것이 목표이다.
• 수렴속도가 빠르지만, 일반적인 뉴턴 메소드에 비해서는 느린 편이다.

이에 해당하는 방법으로는 SR1, DFP, BFGS 등이 있으며, 보통 BFGS 방법이 가장 많이 사용된다.