각도 표현의 미분 불가능 문제와 복소수

그냥 각도 1개 $\theta$를 쓰면 되는데, 다른게 더 필요할까?

자세의 미분 불가능 문제

그냥 각도 쓰지 왜

자세를 단순한 각도1개 (1개의 scalar 값)으로 표현하게 되면 나타나는 여러가지 문제점들이 있다.

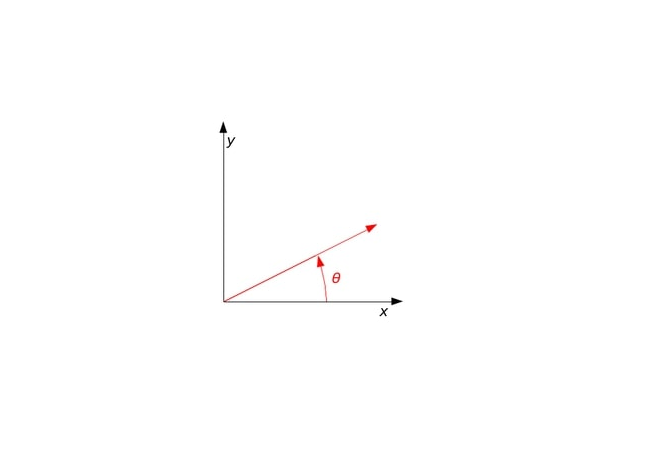
앞서서 2차원 평면의 벡터 회전 행렬이 다음과 같음을 보였다.

\[\begin{equation} R(\theta) = \begin{bmatrix} \cos{\theta} & -\sin{\theta} \\\ \sin{\theta} & \cos{\theta} \end{bmatrix} \label{e0} \end{equation}\]

이 행렬은 1개의 scalar 값 $\theta$에 의해서 회전 변환이 결정됨을 확인할 수 있다.

그렇다면 저런 숫자를 4개씩이나 쓰는 거창한 표기 말고, 그냥 $\theta$로 표현한다음 각도끼리 더하면 되는거 아닌가?

차피 2개의 자세가 있을 때, $R(\theta_1) R(\theta_2) = R(\theta_1 + \theta_2)$의 관계가 성립한다면, 귀찮게 숫자를 4개씩이나 쓰는 행렬 R을 쓰면서 연산량까지 많은 행렬 곱을 사용할 필요가 있을까?
그냥 $\theta_1 + \theta_2$로 계산하면 처음부터 쉬운데 돌아갈 이유가 없다.

하지만, 이 결론에는 치명적인 단점이 있는데, 바로 각도값이 불연속적이라는 것이다.

360은 0이 아니다

어떤 물체를 350° 만큼 돌린 다음, 다시 20°를 추가로 돌렸다고 해보자. 결과물의 각도는 몇도일까?
당연히 2개의 각도를 더한 370°=10°이다. 각도니까.

문제는 이러한 내용을 코드로 옮기거나, 수학으로 옮길 때 문제가 발생한다.

코드상으로는 theta_1 + theta_2를 해서 370이라는 숫자가 될 것이다. 하지만 그 결과값을 10과 비교하면 당연히 다르다고 할 것이다. 왜냐하면 370은 10이 아니니까.
만약 각도값을 계속 꾸준히 더해야 하는 상황에서는 결과물의 자세값이 끊임없이 커지면서 여러 문제를 일으킬 수도 있다. 갈수록 계산량도 쓸데없이 늘리면서 자료형의 범위를 벗어나며 오버플로우를 일으킬 수 있기 때문이다.

수학에서도 마찬가지다. $350+10=370 \neq 10$임은 너무나 당연한 말이지만, 각도이기 때문에 말이 되어야 한다.

이 때문에 로봇 코드에서는 심심찮게 wrap_angle(theta)같은 함수들을 볼 수 있다. 각도와는 달리 360마다 순환하지 못하는 실수의 특성을 강제로 조건문을 통해 바로잡는 샘이다.

미분 불가능 문제

이와 같은 특성 때문에 자세를 표현한 각도를 미분하면 굉장히 이상한 결과가 나온다. 360°=0°으로 바뀌는 순간마다 기울기가 무한대로 치솟게 된다.

예시로, 로봇의 자세 각속도를 구하는 과정에서 현재의 자세값을 그대로 이용하면 문제가 된다.

보통 수치 미분(차분)은 다음과 같이 구해진다.

\[\begin{equation} \large \frac{\theta_{curr} - \theta_{prev}}{\Delta t} \simeq \frac{d\theta}{dt} = \dot{\theta} \label{e1} \end{equation}\]

이때 만약 1초 동안 측정된 각도가 350°->370°였다고 해보자.
위의 \eqref{e1}에 그대로 넣어서 계산해보면 다음과 같다.

\[\begin{equation} \frac{370-350}{1} = 20 \text{ }deg /s \end{equation}\]

하지만 각도값을 저장하는 변수가 360을 넘어서도 계속 커질 수 있게 허용하면, 잠재적으로 오버플로우가 일어날 가능성이 있으므로 보통은 0~360 사이의 값을 저장하게 한다.

따라서 실제로는 350° -> 10° 로 출력되며, 이를 위의 \eqref{e1}에 도로 넣으면 다음과 같다.

\[\begin{equation} \frac{10-350}{1} = -340 \text{ } deg/s \end{equation}\]

이를 해결하려면, 두 각도의 차이를 계산하는 $x_{curr} - x_{prev}$ 부분을 angle_diff_wrap(theta1, theta2)등의 함수로 감싸는 것이다.

하지만 수학적으로는 여전히 불연속이라는 큰 위험성이 남는다.

회전행렬은 미분 가능한가?

회전 행렬 방식으로 표현된 자세는 미분이 가능하며, 다음과 같이 각속도를 구할 수도 있다.

위의 식 \eqref{e0}를 미분하여, 관계를 알아볼 수 있다.

\[\begin{align} \dot{R} &= \frac{dR(\theta)}{dt} \nonumber \\[10pt] &= \frac{d}{dt}\begin{bmatrix} \cos{\theta} & -\sin{\theta} \\\ \sin{\theta} & \cos{\theta} \end{bmatrix} \nonumber \\[10pt] &= \dot{\theta} \begin{bmatrix} -\sin{\theta} & -\cos{\theta} \\\ \cos{\theta} & -\sin{\theta} \end{bmatrix} \nonumber \\[10pt] \dot{R}\begin{bmatrix} -\sin{\theta} & -\cos{\theta} \\\ \cos{\theta} & -\sin{\theta} \end{bmatrix}^{-1} &= \dot{\theta}I \nonumber \end{align}\]

따라서 회전행렬 R과 각속도와의 관계는 다음과 같다.

\[\begin{equation} \dot{R} \begin{bmatrix} -\sin{\theta} & \cos{\theta} \\ -\cos{\theta} & -\sin{\theta} \end{bmatrix} = \dot{\theta}I \label{e2} \end{equation}\]

이제 다시 1초동안 350°->10° 의 예시를 사용하여 식 \eqref{e2}를 검증해 보자.

\[\begin{align} R(350°) &= \begin{bmatrix}0.98481 & 0.17365 \\ -0.17365 & 0.98481\end{bmatrix} \nonumber \\[10pt] R(10°) &= \begin{bmatrix}0.98481 & -0.17365 \\ 0.17365 & 0.98481\end{bmatrix} \nonumber \\[10pt] \dot{R} \simeq \frac{R(10°) - R(350°)}{\Delta t} &= \begin{bmatrix}0 & -0.34730 \\ 0.34729 & 0\end{bmatrix} \nonumber \\[10pt] \dot{R} \cdot \begin{bmatrix} -\sin{350°} & \cos{350°} \\\ -\cos{350°} & -\sin{350°} \end{bmatrix} &= \begin{bmatrix}0 & -0.34730 \\ 0.34729 & 0\end{bmatrix} \begin{bmatrix} 0.17365 & 0.98481 \\ -0.98481 & 0.17365\end{bmatrix} \nonumber\\[10pt] &= \begin{bmatrix} 0.34202 & -0.0603 \\ 0.0603 & 0.34202\end{bmatrix} \nonumber \\[10pt] &\simeq 0.34202 \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}=\dot{\theta}I \nonumber \\[10pt] \therefore \dot{\theta} &= 0.34202 \text{ } rad/s = 19.402\text{ }deg/s \label{e20} \end{align}\]

이처럼 기존의 방식과는 다르게 자연스럽게 각속도를 수치미분을 통해 근사할 수 있다. 다만, $\dot{R}$을 근사하는 과정에서 생기는 오차 때문에 정확히 20°이 나오지 않고 19.402°가 나오는 것이 단점이다.

하지만 이는 컴퓨터의 수치 미분 과정에서 생긴 에러로 인한 것이다.
적어도 식 $\eqref{e2}$의 유도 과정 중 if문은 없었다. 수학적으로는 미분에 대해서 매끄럽게 동작하는 것이다.

곱셈과 복소수

곱셈과 수의 순환

각도를 덧셈으로 자연스럽게 표현하지 못했던 이유는, 360°=0°라는 불연속적인 특성 때문이다. 실수의 덧셈은 순환하지 않으며, 계속 증가하거나 감소할 수만 있기 때문이다.

그렇다면 자연스럽게 수를 순환시키는 연산이 없을까?
우리에게 익숙한 곱셈 중에서 음수의 곱셈은 수를 순환시킬 수 있다.

$a \times -1 = -a$, $-a \times -1 = a$로 계속 순환된다.
곱셈의 이런 특징을 사용해서 자세를 자연스럽게 순환 시킬 수 있을까?

그림 1 : 음수의 곱으로 순환하는 실수

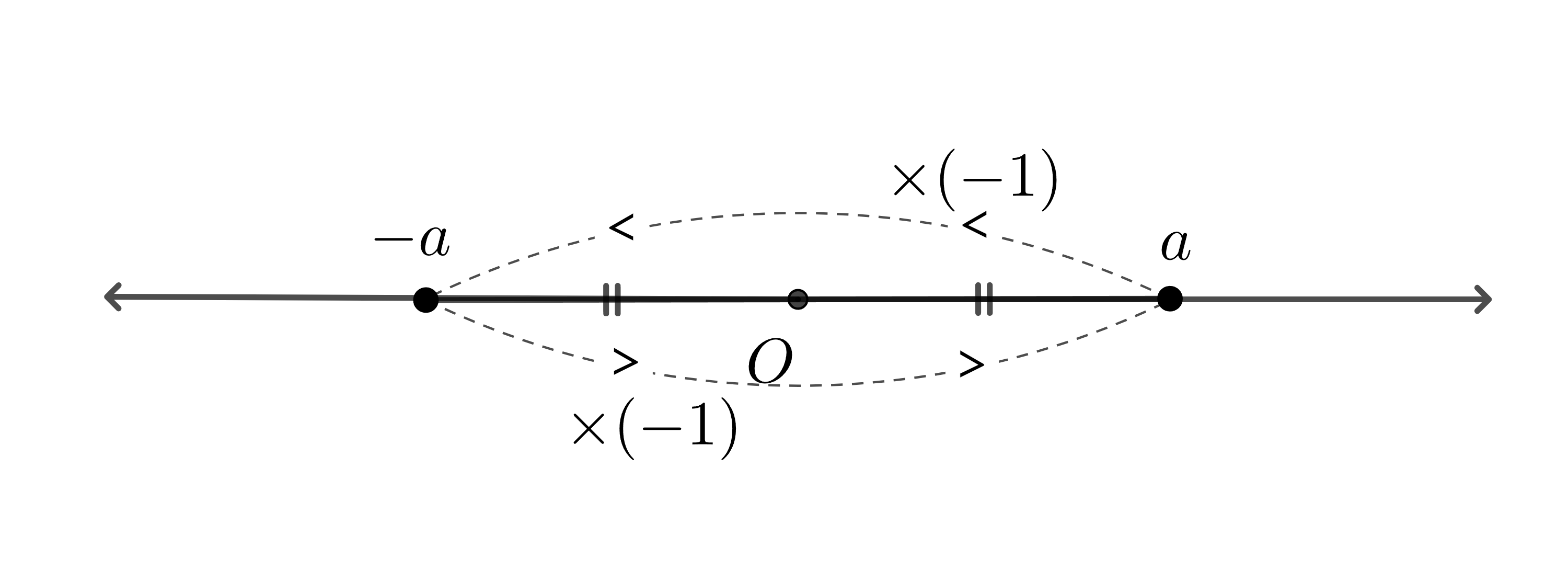
그림 1에서 임의의 숫자 $a$를 수직선상에 표현하였다. 이때, -1을 곱함으로써 원점에 대해서 계속 대칭으로 이동하게 된다.

하지만 만약 이게 각도의 덧셈과 같다면 어떨까?
-1을 곱한다는 것 자체의 의미가 만약 원점에 대해서 대칭으로 점을 옮기는 것이 아니라, 수를 180° 회전시키는 것이라면?

그림 2 : 90° 각도의 수는 무엇일까

그림 2에서 -1을 두번 곱하는 것의 의미를 새롭게 생각해 볼 수 있다.
길이가 $a$인 점을 180°로 두번 돌리면 360°가 되기 때문에, 다시 제자리로 돌아오는 것.

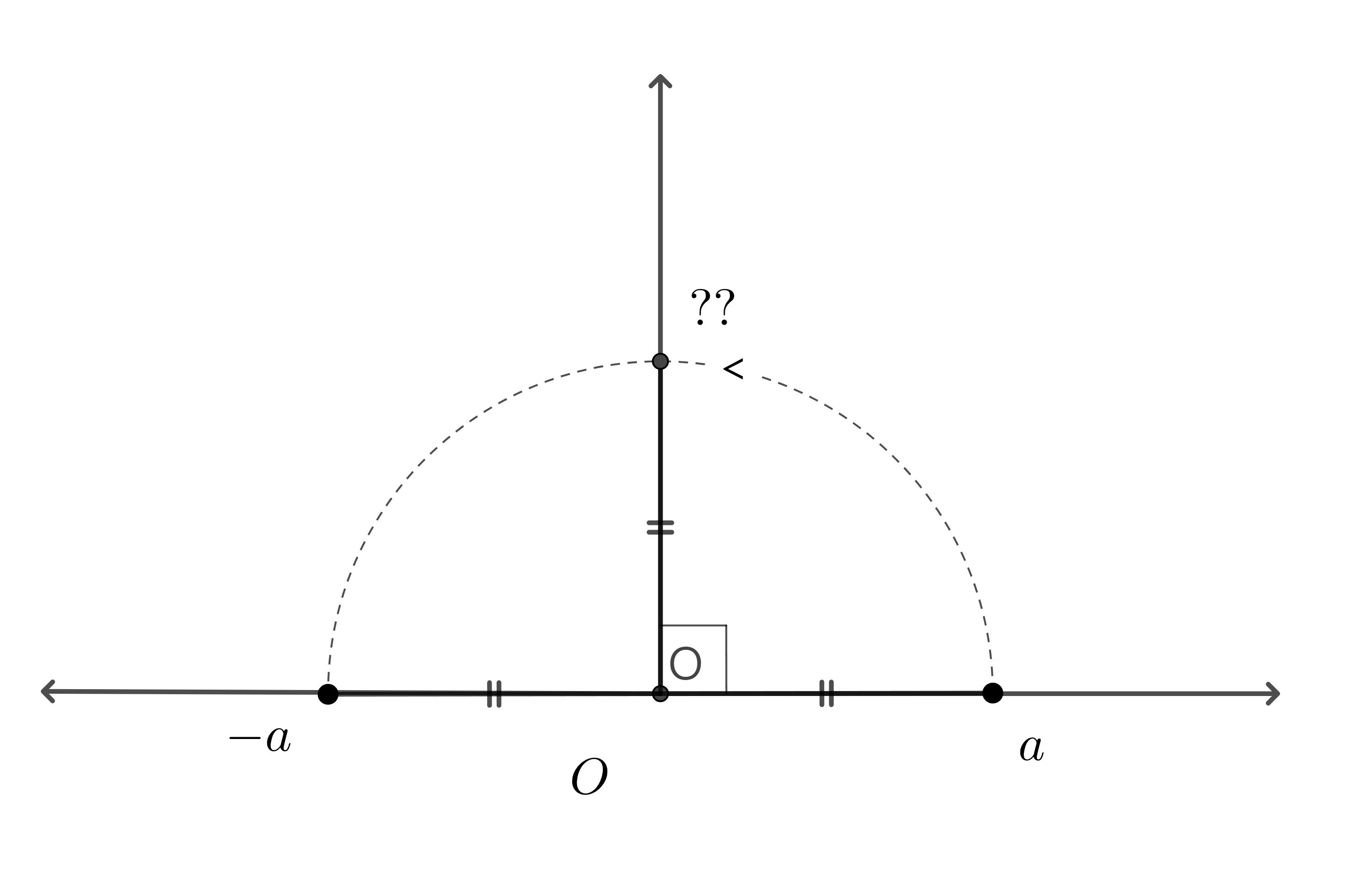
그러면 $a$를 반드시 180°만 돌릴 수 있을까? 90°나 45°, 30°로 돌려진 수는 무엇일까.

우리의 지금까지만의 이야기로 놓고 보면 90°회전을 2번 하면 180° 회전이 된다.
즉, 90° 회전을 나타내는 수를 $x$라고 했을 때, $x^2=-1$이 되어야 한다는 뜻이다.
당연히 실수에 저런 수는 존재하지 않는다.
하지만 고등학교 과정에서 저런 수를 배웠는데, 바로 허수(Imaginary number) 이다.

참고 : Imaginary Number

허수, 복소수와 복소평면

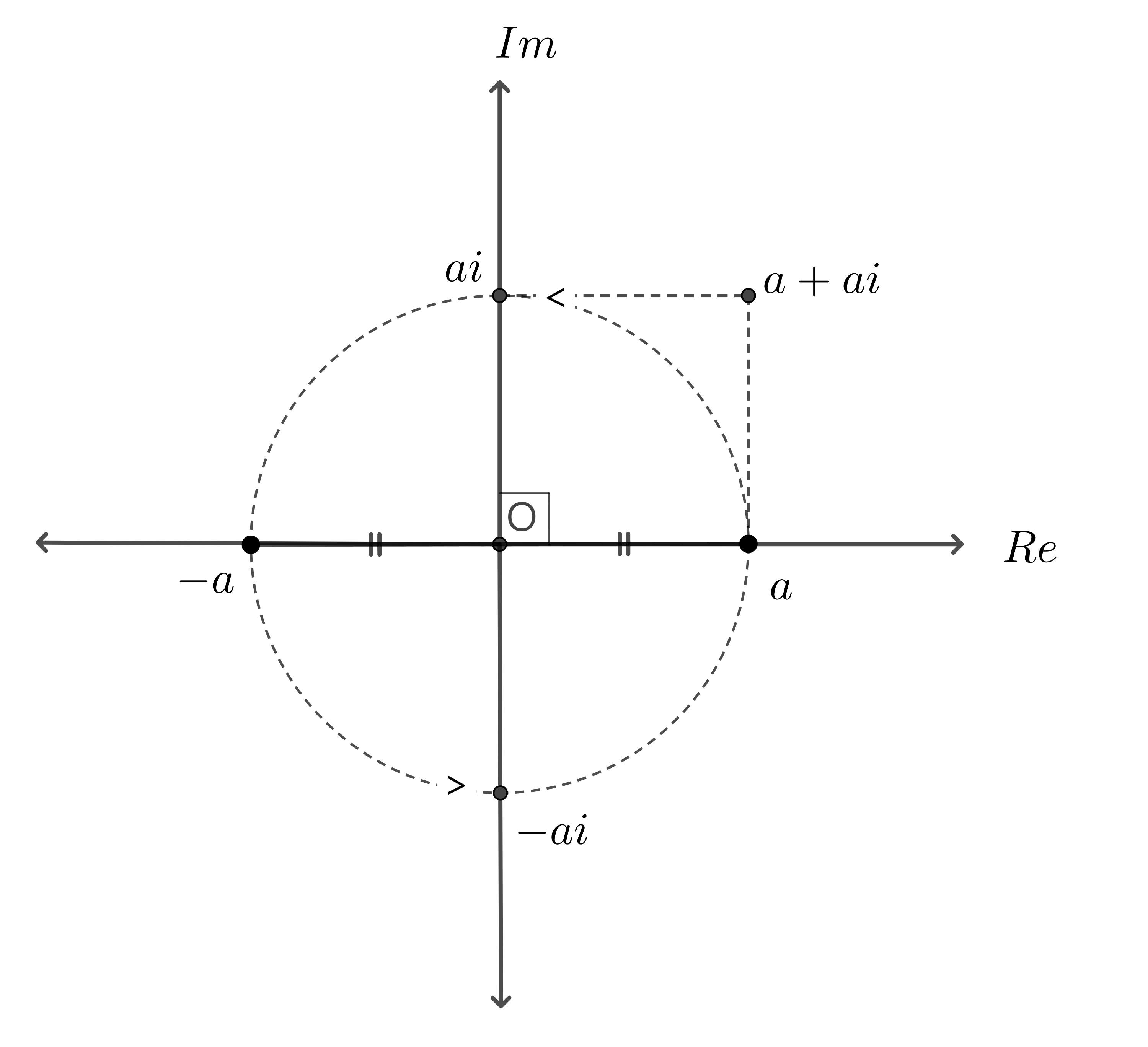
이제 그림2에서 90°도 회전된 이상한 수가 복소수 $i$임을 알아챘다. 그렇다면 45°회전은 이제 아예 축을 벗어나서 평면상에 존재하게 된다.
마치 좌표계의 2개의 축벡터를 더해서 표시하는 것 처럼, 1개의 실수축과 1개의 허수축을 더하여 저 평면상의 점의 위치를 표시할 수 있다.

따라서 그림2는 다음과 같이 실수축과 허수축으로 표현된 2차원 평면으로 바뀐다.

그림 3 : 실수축과 허수축으로 이루어진 2차원 평면

이를 복소평면 이라 하며, 이 평면상에 표시되는 수를 복소수(Complex Number)라 한다.

이렇게 정의된 새로운 수, 복소수$z$의 정의는 다음과 같다.

\[\begin{align} z = a+bi, \text{ } (a,b \in \mathbb{R}, i^2 = -1) \end{align}\]

이떄 $a$를 $z$의 실수부(Real Part)라 하며 통상 $Re(z)$로 표현한다.
$b$는 $z$의 허수부(Imaginary Part)라 하며 통상 $Im(z)$로 표현한다.
또한, $a = 0$인 경우를 순허수(Pure Imaginary Number)라 하며, $b = 0$인 경우는 기존과 같이 실수(Real Number)라 한다.

두 복소수의 곱 $(a+bi)(c+di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i$ 로 연산된다.

그리고 켤레 복소수(Complex Conjugate)는 $\bar{z}$로 표현되며, 허수부의 부호를 바꾸는 연산이다.
$\overline{z} =\overline{a+bi} = a-bi$

복소수의 곱의 기하학적 의미

기존의 실수에도 수의 크기(절대값)이 있었듯이, 복소수도 수이므로 크기가 있다.
$\left\vert z \right\vert = \left\vert a+bi \right\vert = \sqrt{a^2 + b^2}$로 계산되며, 이는 우리가 기존에 2차원 평면상에 있던 벡터의 크기를 계산하는 방식과 같다. 따라서 $z \times \bar{z} = \left\vert z \right\vert^2$ 가 된다.
물론 평면상의 벡터처럼 각도값도 가지고 있으며, 이를 복소수 z의 편각(argument)이라 하고 통상 $arg(z)$로 표현한다.

그렇다면 이제 길이가 $r$이고 편각이 $\theta$인 복소수를 $z(r, \theta)$ 라 했을 때, 그 값을 알아볼 수 있다.

\[\begin{equation} z(r, \theta) = r(\cos{\theta} + \sin{\theta}i) \end{equation}\]

이를 복소수의 극형식(Polar Form) 이라 한다. 길이와 편각 만으로 표현했기 때문에 마치 극좌표계와 비슷해서 이런 이름이 붙었다.

그렇다면 2개의 복소수, $z(l_1, \theta_1), z(l_2, \theta_2)$를 곱하면 어떻게 될까?
매우 재미있는 결과를 확인할 수 있다.

\[\begin{align} z(l_1, \theta_1) &= l_1\left(\cos(\theta_1) + \sin{\theta_1}\right) \nonumber \\[5pt] z(l_2, \theta_2) &= l_2\left(\cos(\theta_2) + \sin{\theta_2}\right) \nonumber \\[5pt] z(l_1, \theta_1) \times z(l_2, \theta_2) &= l_1 l_2 \left( (\cos{\theta_1} \cos{\theta_2} - \sin{\theta_1} \sin{\theta_2}) + (\sin{\theta_1} \cos{\theta_2} + \cos{\theta_1} \sin{\theta_2})i\right) \nonumber \\[5pt] &= l_1 l_2 \cos{\left(\theta_1 + \theta_2 \right)} + l_1 l_2\sin{\left(\theta_1 + \theta_2\right)}i \nonumber \\[5pt] &= z(l_1 l_2, \theta_1 + \theta_2) \label{e3} \end{align}\]

위 식 $\eqref{e3}$를 통해 2개의 복소수를 곱하면, 길이는 곱해지고, 편각은 더해짐을 보였다.

이때, 만약 $l_2=1$이라면?,
마치 회전 변환 처럼 기존의 복소수를 회전하는 변환이 된다.

따라서 어떠한 복소수 z를 곱했을 때 결과가 $\theta$ 만큼 돌리는 회전 변환이 될 조건은 다음과 같다.

\[\begin{equation} \left\vert z \right\vert = 1, arg(z) = \theta \end{equation}\]

어떻게 보면 자세를 표현하는 복소수라 봐도 된다.

복소수 곱셈의 행렬 표현

복소수를 행렬로 표현하면 통상 다음과 같이 표현한다.

\[\begin{equation} z = a+bi= \begin{bmatrix} a \\ b \end{bmatrix} \end{equation}\]

복소수를 곱하는 연산도 행렬로 표현될 수 있을까?

두 복소수의 곱 $(a+bi)(c+di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i$ 로 연산된다. 이를 행렬을 이용해서 표현하면 다음과 같다.

\[\begin{align} (a+bi)\times(c+di) &=> \begin{bmatrix} ? & ? \\ ? & ? \end{bmatrix} \begin{bmatrix} c \\ d \end{bmatrix} \nonumber \\[10pt] &= \begin{bmatrix} a & -b \\ b & a \end{bmatrix} \begin{bmatrix} c \\ d \end{bmatrix} = \begin{bmatrix} ac - bd \\ ad + bc \end{bmatrix} \nonumber \\[10pt] &=> (ac - bd) + (ad + bc)i \nonumber \end{align}\]

또는 이렇게 유도할 수도 있다.

\[\begin{align} \begin{bmatrix} 1/1 & 1/i \\ i/1 & i/i \end{bmatrix} \begin{bmatrix} 1 \\ i \end{bmatrix} &= \begin{bmatrix} \text{Real Part} \\ \text{Img Part} \end{bmatrix} \nonumber \\[10pt] \therefore \begin{bmatrix} 1/1 & 1/i \\ i/1 & i/i \end{bmatrix} &= \begin{bmatrix} 1 & -i \\ i & 1 \end{bmatrix} \nonumber \\[10pt] &= \begin{bmatrix} a & -b\\ b & a \end{bmatrix} \nonumber \end{align}\]

이를 정리하면 복소수의 곱셈 행렬은 다음과 같다.

\[\begin{align} z\times z_1 &<=> [z]_{\times} z_1 \text{ (Matrix form)} \nonumber \\[10pt] \text{if }z&=a+bi, \nonumber \\[10pt] [z]_{\times} &= \begin{bmatrix} a & -b \\ b & a \end{bmatrix} = \begin{bmatrix} Re(z) & -Im(z) \\ Im(z) & Re(z) \end{bmatrix} \label{e4} \end{align}\]

이제 식$\eqref{e4}$에 $z$를 길이가 1이고 편각이 $\theta$인 복소수로 바꾸면 익숙한 회전 행렬이 또 보인다.

\[\begin{align} z(1, \theta) &= \cos{\theta} + \sin{\theta}i , \nonumber \\[10pt] [z]_{\times} &= \begin{bmatrix} Re(z) & -Im(z) \\ Im(z) & Re(z) \end{bmatrix} \nonumber \\[10pt] &= \begin{bmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{bmatrix} = R(\theta) \end{align}\]

복소수의 미분과 각속도

결국 회전 행렬의 형태로 또 표현되므로, 미분을 통한 각속도 역시 만들어낼 수 있다.

\[\begin{align} z &= \cos{\theta}+\sin{\theta}i, \nonumber \\ \dot{z}&= -\dot{\theta}\sin{\theta} + \dot{\theta}\cos{\theta}i \nonumber \\ &= \dot{\theta} i \left( \cos{\theta} + \sin{\theta} \right) \nonumber \\ &= \dot{\theta} i \cdot z \\ \nonumber \\ => \dot{z}\cdot \bar{z} &= \dot{\theta} i \cdot z \cdot \bar{z} \nonumber\\ &= \dot{\theta} i \left\vert z \right\vert^2 \nonumber \\ &= \dot{\theta} i \end{align}\]

따라서 길이가 1인 복소수와 각속도의 관계는 다음과 같다

\[\begin{equation} \dot{z}\cdot\bar{z} = \dot{\theta} i \label{e5} \end{equation}\]

아까 $\eqref{e20}$의 예시로 식 $\eqref{e5}$ 가 맞는지 계산 해 보겠다.

\[\begin{align} z_{350} = \cos{350°}+\sin{350°}i &= 0.98481 - 0.17365i \nonumber \\ z_{10} = \cos{10°} + \sin{10°}i &= 0.98481 + 0.17365i \nonumber \\ \dot{z} \simeq \frac{z_{10} - z_{350}}{\Delta t} &= 0.34729i \nonumber \\[8pt] \overline{z_{10}} &= 0.98481 + 0.17365i \nonumber \\ \nonumber \\ \dot{z} \cdot \overline{z} & = -0.060307 + 0.34201i \simeq 0.34201 i \nonumber \\ &= \dot{\theta} i \nonumber \\ \nonumber \\ \therefore \dot{\theta} &= 0.34201 \text{ }rad/s = 19.59573 \text{ } deg/s \end{align}\]

이전의 계산 결과와 비슷한, 19.596°가 나왔다. 20°가 아닌 이유는 아까와 비슷하게, $\dot{z}$를 근사하는 과정에서 생긴 오차가 반영된 것이다.
하지만 식 $\eqref{e5}$도 중간에 if와 같은 조건문이 없이 매끄럽게 미분되어 유도된다.

더 이상 행렬이 아니라 ‘수’ 그 자체를 사용하여 자세를 표현하고 합성할 수 있게 되었다는 점에서 회전 행렬을 사용한 것과는 또 다른 의의가 있다.