최적화 이론 소개
최적화란 무엇이고 왜 필요한가
참고 : 모두를 위한 컨벡스 최적화
이 카테고리의 거의 모든 내용은 모두를 위한 컨벡스 최적화 깃허브 페이지의 내용을 내가 공부하면서 정리한 것이다. 더 자세한 이론적인 내용은 위 링크를 참고하면 좋다.
최적화 문제의 정의
최적화는 어떤 함수의 값을 최소화 또는 최대화시키는 입력 변수들의 값을 찾는 것이다. 이때 최적화의 대상이 되는 함수는 목적함수(objective function)또는 손실함수(cost function) 이라고 부르며, 입력 변수들의 값은 최적화 변수(optimization variable)라고 부른다.
수학적으로 최적화 문제는 다음과 같이 정의된다.
Mathmatical Optimization Problem in standard form :
\[\begin{align} \min_x{f(x)} \\ \text{s.t. } g_i(x) &\leq 0, \quad i = 1, \ldots, m \nonumber \\ h_i(x) &= 0, \quad i = 1, \ldots, r \nonumber \end{align}\]
이 형태에서 각각의 부분은 다음과 같이 불린다.
- $x \in \mathbb{R}^n$ : 최적화 변수(optimization variable)
- $f : \mathbb{R}^n \rightarrow \mathbb{R}$ : 목적함수(objective function)
- $g_i : \mathbb{R}^n \rightarrow \mathbb{R}$ : 부등식 제약조건(inequality constraints)
- $h_i : \mathbb{R}^n \rightarrow \mathbb{R}$ : 등식 제약조건(equality constraints)
$x \in \mathbb{R}^n$ : 실수 n차원 벡터 $x$
$f : \mathbb{R}^n \rightarrow \mathbb{R}$ : 실수 n차원 벡터를 받아 실수를 반환하는 함수 $f$
이떄, 위의 제약 조건들을 전부 만족하는 영역을 $D$(feasible domain)이라 한다.이 feasiblie domain 안에서 cost function을 최소로 만드는 벡터는 보통 $x^* $라 표현하고, 이를 optimal solution 이라 한다. (당연히 $x^* \in D$ 이다)
대부분의 상황에서 optimal value 보다는 optimal solution, $ x^* $ 을 찾는 것에 더 관심이 많다. 어차피 $x^* $ 을 알아낸 순간, $f(x^{*})$ 을 하면 되니까.
예시 1 - 단순한 목적 함수
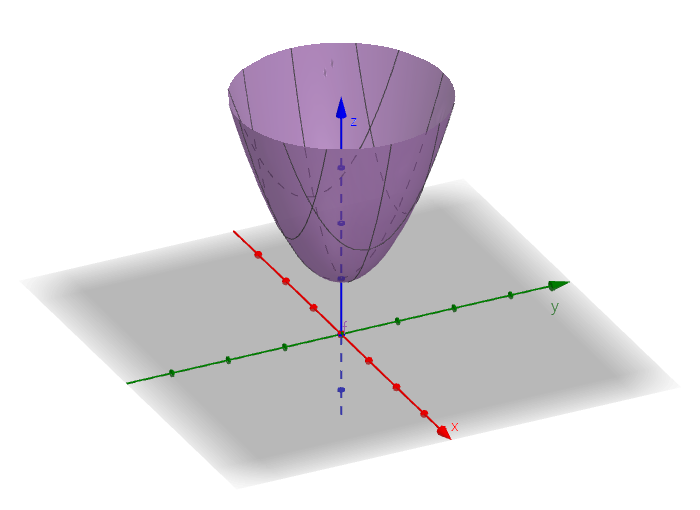
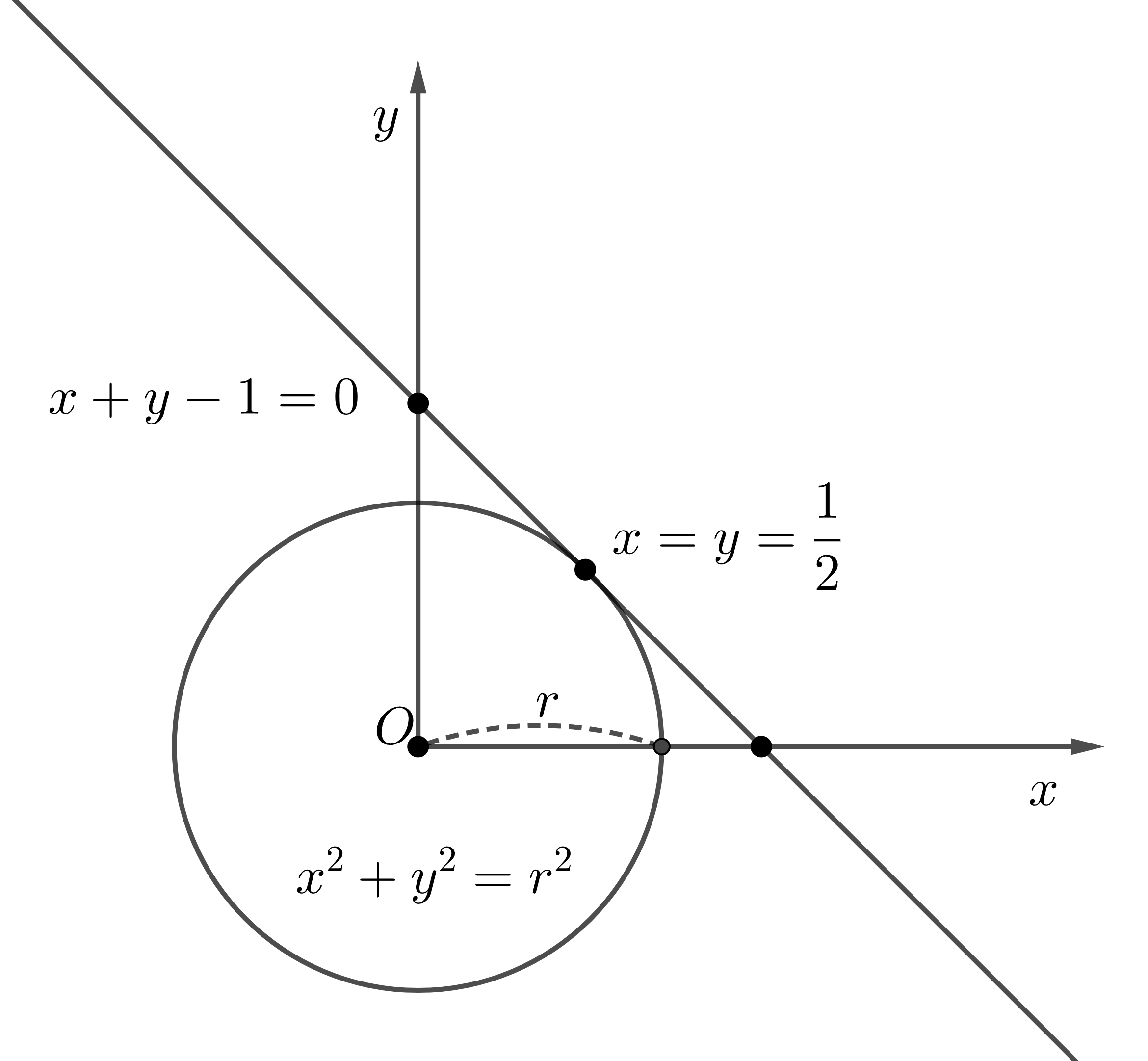
$x = \begin{bmatrix}a & b\end{bmatrix}^T \in \mathbb{R}^2$, $f(x) = a^2 + b^2$ 일때, $f(x)$를 최소화하는 $x$를 찾는 문제를 생각해보자. 이때, $g_1(x) = a + b - 1 = 0$ 이라는 제약조건이 있다고 하자. 이때, 위의 최적화 문제는 다음과 같이 정의된다.
\[\begin{align} \min_{a,b}{a^2 + b^2} & \\ \text{s.t. } a + b - 1 &= 0 \nonumber \\ \end{align}\]간단하게 중학 수학을 사용해 풀어보면, 다음과 같다 :
\[\begin{align} a &= 1 - b \nonumber \\ a^2 + b^2 &= (1-b)^2 + b^2 = 1 - 2b + b^2 + b^2 = 2b^2 - 2b + 1 \nonumber \\ &= 2(b - \frac{1}{2})^2 + \frac{1}{2} \geq \frac{1}{2} \\ \nonumber \\ \therefore a = b &=\frac{1}{2}, f(a,b) = \frac{1}{2}, \text{minimized} \end{align}\]또는 $a^2 + b^2 = r^2$임을 사용해서, 중심이 원점이고 반지름이 $r$인 원이라고 생각하면, 기하 문제로 바꿀 수도 있다 :
이렇게 최적화 문제는 다양한 방법으로 해결될 수 있지만,
조금만 복잡해지면 기존의 방법들이 매우 힘들게 된다
예시 2 - 복잡한 목적 함수
예를 들어, 이런 문제는 어떨까 :
\[\begin{align} x &= \begin{bmatrix}a & b & c & d\end{bmatrix}^T \in \mathbb{R}^4 \\ f(x) &= 3a^2 + 3b^2 + 4c^2 + d^2 + 4bc +2bd+2ad-2+13 \nonumber \\ \nonumber \\ & \min_{x}{f(x)} & \\ \end{align}\]제약 조건이 없어서 변수의 개수를 줄일 수도 없으며, 변수의 개수도 4개이기 때문에 4차원 그래프를 그릴 수도 없다. 애초에 답이 있긴 한건지도 애매하다.
여기서 눈썰미가 좋은 사람이라면, 다음 식을 전개한 형태라는 것을 알아차릴 수 있다 :
\[\begin{align} f(x) &= (a-1)^2 + (a-b)^2 + (b+2c)^2 + (a+b+d)^2 + 12 \\ \nonumber \\ \therefore f(x) & \text{ minimized at : } a=1, b=1, c=-0.5, d=-2, \nonumber \\ x^* &= \begin{bmatrix}1 & 1 & -0.5 & -2\end{bmatrix}^T \end{align}\]하지만 매번 이럴 순 없다. 변수가 100개라면? 1천개라면? 저렇게 제곱식으로 묶인다는 보장이 있는가?
이런 문제를 해결하기 위해 나온 것이 바로 최적화이다. 최적화는 이러한 문제를 분류하여 다양한 해결책과 방법을 제시하고 있다. 쉬운 문제의 경우에는 아예 closed form으로 정답이 나오기도 하고. 수치해석적으로 접근하여 근사해를 구할 수도 있다.
최적화의 종류
기본 분류
최적화 문제는 목적 함수, 제약 조건의 형태에 따라 다양한 종류로 나뉜다.
Linear Programming (LP)
목적 함수가 선형 함수인 경우. 선형 계획법 이라고도 하며, 효율적이고 단순한 알고리즘들이 많아 널리 사용된다.Quadratic Programming (QP)
목적 함수가 이차 함수인 경우. 경제나 공학 분야에서 자주 사용된다. 특히 공학에서는 목적 함수로 원하는 값과의 오차제곱합을 자주 사용한다.Quadratically Constrained Quadratic Programming (QCQP)
목적 함수와 제약 조건이 모두 이차 함수인 경우.Mixed Integer Linear Programming (MILP)
특정 최적화 변수가 정수로 한정되며, 목적 함수는 선형 함수인 경우. knapsack problem 등이 이 문제에 해당된다. 한다 안한다(o,x의 문제). 물건을 몇개를 사용한다(반드시 정수개수) 등의 제약이 추가로 걸리는 최적화 문제이다.Mixed Integer Quadratic Programming (MIQP) 특정 최적화 변수가 정수로 한정되며, 목적 함수는 이차 함수인 경우.
Nonlinear Programming (NLP)
목적 함수가 비선형 함수인 경우. 비선형 시스템의 최적제어 등에서 볼 수 있다. 그 외에도 많은 문제들이 비선형성을 갖고 있다.
이 외에도 더 많은 종류가 있다 (Semidefinite , Conic)
컨벡스 최적화(Convex Optimization)
위의 경우 중, 목적 함수와 제약 조건의 모양이 전부 볼록, 또는 오목한 경우에 해당한다. 이 경우에 local minimum이 global minimum이 되므로 optimial solution을 찾는데에 매우 유리하다. 그 외에도 유용한 특성들이 많아 더 효율적인 계산 방법들이 많이 연구되어 있다.
컨벡스 최적화는 다음과 같은 형태로 정의된다 :
\[\begin{align} \min_{x \in D } \quad & f(x) \\ \text{s.t. } \quad & g_i(x) \leq 0, \quad i = 1, \ldots, m \nonumber \\ & h_i(x) = 0, \quad i = 1, \ldots, r \nonumber \\ \nonumber \\ f, g_i &: \text{convex function}, \\ h_i &: \text{affine function} \end{align}\]아핀 함수(affine function)는 다음과 같이 선형항에 상수가 더해진 형태로 정의된다 :
\[\begin{align} h_i = a_i^T x + b_i \end{align}\]볼록 함수(convex function)는 다음과 같이 정의된다 :
\[\begin{align} f(\theta x + (1-\theta)y) \leq \theta f(x) + (1-\theta)f(y), \quad \forall x,y \in D, \theta \in [0,1] \end{align}\]위에서 예시로 든 최적화도 전부 컨벡스 최적화에 속한다.