Quasi-Newton method

경사 하강법보다 일반적으로 더 빠른 수렴속도를 가진 Newton’s method 에 대해 알아본다.

참고 1 : Quasi-Newton method
참고 2 : 모두를 위한 컨벡스 최적화, Quasi-Newton method
참고 3 : CMU-convex optimiazation, Quasi-Newton method

기존 Newton method의 단점

Newton method는 2차 근사를 사용하여 수렴하기 때문에, 경사하강법 보다 빠른 수렴속도를 가진다는 장점이 있다.
그럼에도 불구하고 여러가지 단점이 있는데. 바로 메모리와 계산량이 많다는 것이다.

다음 벡터 $x \in \mathbb{R}^n$과 2번 미분 가능한 함수 $f : \mathbb{R}^n \rightarrow \mathbb{R}$을 고려하자. 현재 위치가 $x$일 때, Newton method를 적용하면 다음 위치 $x^+$는 다음과 같이 주어진다 :

\[\begin{align} x^+ = x - \nabla^2 f(x)^{-1} \nabla f(x) \end{align}\]

여기서 볼 수 있는 단점은 다음과 같다

1. 헤시안 행렬의 메모리 사용량
   $\nabla^2 f$를 계산하는 것도 꽤 걸리지만, $n \times n$의 크기를 가진 행렬이기 때문에, $O(n^2)$의 메모리를 사용한다. 이는 매우 큰 차원에서는 큰 문제가 된다.

2. 큰 행렬의 역행렬 계산
   $\nabla^2 f(x)^{-1}$은 $n \times n$ 행렬의 역행렬을 계산해야 한다. 이 역시 매우 큰 차원에서는 계산량을 잔뜩 잡아먹는다.

Quasi-Newton method

핵심 개념

위의 단점들을 해결하기 위해 나온 것이 Quasi-Newton method다.

핵심 아이디어는 $\nabla^2 f(x)^{-1}$ 를 직접 계산하지 않고, 근사하는 것이다. 즉, 다음 위치를 업데이트 할 때, 헤시안 행렬의 역행렬 대신, 다른 행렬 $B$를 사용하여 근사한다.

즉 다음과 같은 절차를 가진다 :

Quasi-Newton method

1. 초기 $x_0$과 $B_0$을 설정한다
2. $B_k p_k = -\nabla f(x_k)$ 를 푼다
3. step size $t_k$를 고르고, $x_{k+1}=x_k+t_k p_k$ 로 업데이트 한다
4. $B_{k}$를 $B_{k+1}$로 업데이트 한다.
5. 수렴될 때 까지 2,3,4의 절차를 반복한다.

여기서 $B_k$는 $k$번째 근사 헤시안 행렬이다. 이를 어떻게 업데이트 할 것인가가 Quasi-Newton method의 핵심이다.

이때, $B_k$가 헤시안 행렬과 비슷하게 행동하기 위해서는 다음 몇가지 조건을 만족해야 한다.

approx Hessian matrix $B, B^+$의 조건

1. $B$는 대칭 행렬(symmetric matrix)여야 한다. ($B=B^T$)
   헤시안 행렬은 미분 가능한 연속 함수에 대해 대칭행렬이기 때문이다.
2. $B^+$은 최대한 $B$와 가깝게 업데이트 해야 한다.
   수많은 $B^+$ 후보들 중에서 하나의 $B^+$를 고르는 조건이다. 동시에 후술할 Secant equation과 curvature condition을 만족해야 한다.
3. $B \succ 0$, positive definite 해야 한다.
   convex 함수의 헤시안 행렬 처럼 global optimum을 보장하기 위해서 필요하다.

Secant Equation

어떤 행렬 $B$가 헤시안 행렬과 비슷하게 행동하기 위해서는 다음 등식을 만족해야 한다.

두번 미분 가능한 함수 $f : \mathbb{R}^n \rightarrow \mathbb{R}$과, 벡터 $x \in \mathbb{R}^n$이 있다. newton method를 진행하는 동안, $k$ 번째 벡터를 $x_k$라 하고. $x_{k+1} = x_k + s_k$라 하자.

이때 $\nabla f(x)$의 점 $x_k$ 에서의 1차 테일러 근사를 생각해보자 :

\[\begin{align} \nabla f(x) &\approx \nabla f(x_k) + \nabla^2 f(x_k) (x - x_k) \\ \Rightarrow \nabla f(x_k + s_k) &\approx \nabla f(x_k) + \nabla^2 f(x_k) s_k \\ \end{align}\]

다음으로 $\nabla^2 f(x_k) \approx B_{k+1}$, $\nabla f(x_{k+1}) - \nabla f(x_k) = y_k$ 라 하자.
이제 $B_{k+1}$은 다음을 만족해야 한다.

\[\begin{align} \nabla f(x_k + s_k) &= \nabla f(x_k) + B_{k+1} s_k \nonumber \\ \Rightarrow \nabla f(x_{k+1}) &= \nabla f(x_k) + B_{k+1} s_k \nonumber \\ \Rightarrow \nabla f(x_{k+1}) - \nabla f(x_k) &= B_{k+1} s_k \nonumber \\ \Rightarrow y_k &= B_{k+1} s_k \label{secant-eq} \end{align}\]

위의 식 $(\ref{secant-eq})$를 Secant equation이라고 한다.

이는 마치 두 점, $(x_k, \nabla f(x_k))$와 $(x_{k+1}, \nabla(x_{k+1}))$ 사이의 기울기와 같다.

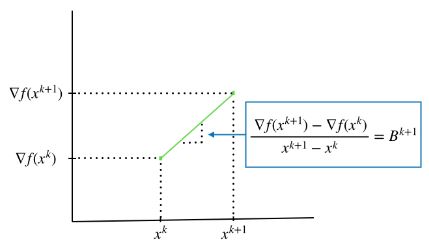secant equation의 기하적인 해석. 출처

Curvature Condition

$B \succ 0$ 이려면, $x^T B x >0$을 항상 만족해야 한다. 이전의 Secant equation ($\ref{secant-eq}$)를 이용해서 curvature condition을 정의할 수 있다 :

\[\begin{align} s_k^T y_k = s_k^T B s_k&> 0 \label{curvature-cond} \end{align}\]

위 조건을 만족하면, Secant equation으로 구해진 $B$는 언제나 positive definite 행렬이 된다.

SR1(Symmetric Rank-1)

핵심 아이디어

가장 간단한 Quasi-Newton method 중 하나인 SR1 방법을 살펴보자.

SR1 방법은 대칭 랭크 1 이라는 이름에 걸맞게, $B_k$를 업데이트 할 때, rank 1짜리 대칭 행렬로 업데이트 한다.

Rank가 1인 대칭 행렬은 다음과 같이 표현할 수 있다.

\[\begin{align} \Delta B = \alpha u u^T, \alpha \in (-1, 1), u \in \mathbb{R}^n \end{align}\]

이때 $\Delta B^T = \alpha (u u^T)^T = \alpha u u^T = \Delta B$이므로 대칭 행렬이다.
또한, $u u^T$는 반드시 rank 1을 가지는데, 다음과 같이 보일 수 있다 :

\[\begin{align} u u^T &= \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} \begin{bmatrix} u_1 & u_2 & \cdots & u_n \end{bmatrix} \nonumber \\ &= \begin{bmatrix} u_1 u_1 & u_1 u_2 & \cdots & u_1 u_n \\ u_2 u_1 & u_2 u_2 & \cdots & u_2 u_n \\ \vdots & \vdots & \ddots & \vdots \\ u_n u_1 & u_n u_2 & \cdots & u_n u_n \end{bmatrix} \\ i \text{th row : } & \begin{bmatrix}u_iu_1 & u_i u_2 & \cdots & u_i u_n \end{bmatrix} = r_i \nonumber \\ j \text{th row : } & \begin{bmatrix} u_j u_1 & u_j u_2 & \cdots & u_j u_n \end{bmatrix} = r_j \nonumber \\ \Rightarrow & u_j r_i = u_i r_j, \forall i,j, \text{ all rows are linearly dependent} \nonumber \\ \therefore uu^T &\text{ : rank 1 matrix} \end{align}\]

따라서 SR1에서 노리는 $B^+$ 업데이트 방법은 이렇게 표현된다

\[\begin{align} B^+ = B + \alpha u u^T \end{align}\]

유도

이때, 위 식은 secant equation을 만족해야 한다. 따라서 다음을 만족해야 한다 :

\[\begin{align} B^+ s &= y \nonumber \\ \Rightarrow B s+ \alpha u u^T s &= y \label{sr1-1} \\ \Rightarrow a (u^Ts )u &= y - Bs \nonumber \\ \Rightarrow u &= \frac{y - Bs}{u^Ts} = \delta (y-Bs), \delta \in \mathbb{R} \label{sr1-2} \\ \Rightarrow & \text{put } (\ref{sr1-2}) \text{ into } (\ref{sr1-1}), \nonumber \\ \Rightarrow y-Bs &= \alpha \delta^2 [s^T(y-Bs)](y-Bs) \label{sr1-3} \end{align}\]

위 식 $(\ref{sr1-3})$을 만족하는 $u$와 $\alpha$를 찾으면, SR1 방법으로 $B^+$를 업데이트 할 수 있다. 각각 다음과 같다 :

\[\begin{align} \alpha &= \text{sign}[s^T(y-Bs)], \quad \delta = \pm (s^T(y-Bs))^{-1/2} \label{sr1-4} \end{align}\]

식 $\ref{sr1-4}, \ref{sr1-2}$를 $\ref{sr1-1}$에 대입하면 다음 결과를 얻는다 :

\[\begin{align} I &= \alpha \delta^2 [s^T(y-Bs)] , \\ \nonumber \\ B^+ &= B + \alpha \delta^2 (y-Bs)(y-Bs)^T \nonumber \\ &= B + \alpha \delta^2 s^T (y-Bs)\frac{(y-Bs)(y-Bs)^T}{s^T (y-Bs)} \nonumber \\ &= B + \frac{(y-Bs)(y-Bs)^T}{(y-Bs)^T s} \label{sr1-5} \end{align}\]

이로써 $B_{k+1}$로의 업데이트 식을 구했다.

마지막으로 $(B^+)^{-1}$에 대해 생각해보자. 어차피 우리가 필요한 것은 $B^{-1}$이니 처음부터 $B_k^{-1}$ 와 $B_{k+1}^{-1}$의 관계로 식을 바꾸면 역행렬을 구할 필요도 없어진다.

식 $\ref{sr1-5}$의 양변을 역행렬로 바꾸면 되는데, 이때 sherman-Morrison formula를 사용하면 된다 :

\[\begin{align} \text{ Sherman-Morrison formula} \nonumber \\ (A + uv^T)^{-1} = A^{-1} - \frac{A^{-1}uv^TB^{-1}}{1+v^TB^{-1}u} \end{align}\]

$B_k^{-1} = H_k$라 하면, $B_{k+1}^{-1}$은 다음과 같이 바뀐다 :

SR1 update

\[\begin{align} H^+ &= H + \frac{(s-H y)(s-H y)^T}{(s-H y)^T s} \nonumber \\ \end{align}\]

단점

치명적인 단점이 2가지가 있다.

1. $(y-Bs)^Ts$가 0 근처일 경우 발산하거나 실패할 수 있다
2. $B, H$가 positive definite를 유지하지 못한다.

이를 보완하기 위해 나온 방법으로 DFP와 BFGS가 있다.

DFP(Davidon-Fletcher-Powell)

동기

DFP는 SR1의 단점을 보완하기 위해 나온 방법이다. rank 2의 symmetric matrix로 매번 $B^{-1}$을 업데이트 하는 방법이다.
이때 $H^+$는 다음과 같이 표현된다.

\[\begin{align} H^+ = H + a u u^T + b v v^T \label{dfp-0} \end{align}\]

유도

secant equation에 의해서, $B^+s=y \Rightarrow s = H^+ y$가 되므로 다음이 성립한다 :

\[\begin{align} H^+y &= (H + a u u^T + b v v^T)y = s \nonumber \\ \Rightarrow s - Hy &= auu^T + bvv^Ty \label{dfp-1} \\ \end{align}\]

이때 $u = s, v = Hs$라 하고 식 $\ref{dfp-1}$ 에 의해 $a,b$를 고르면,

\[\begin{align} s-Hy &= ass^Ty + b Hs(Hs)^Ty \nonumber \\ &= a (s^Ty)s + b \left[(Hs)^T y \right](Hs) \nonumber \\ \\ \therefore a &=\frac{1}{s^Ty}, b = \frac{-1}{(Hs)^Ty} \end{align}\]

이를 다시 식 $\ref{dfp-0}$에 대입하면,

DFP(Davidon-Fletcher-Powell) update

\[\begin{align} H^+ &= H + \frac{ss^T}{s^Ty} - \frac{Hss^TH}{(Hs)^Ty} \label{dfp-3} \\ \end{align}\]

이로써 DFP의 업데이트 식을 구할 수 있다.

다른 유도 방식으로는 Frobenious norm을 최소화 하도록 하는 방법이 있다.

참고

Positive Definite 보장

DFP는 $B$의 positive definite를 보장한다.

기존의 $H$에 대한 업데이트 식을 다시 살펴보자. Woodbury matrix identity를 이용하면 다음과 같이 표현할 수 있다.

\[\begin{align} B^+ &= B + \frac{(y-Bs)y^T}{y^Ts} + \frac{y(y-Bs)^T}{y^Ts} - \frac{(y-Bs)^Ts}{(y^Ts)^2} yy^T \nonumber \\[1em] &= \left( I - \frac{ys^T}{y^Ts} \right) B \left( I - \frac{sy^T}{y^Ts} \right) + \frac{yy^T}{y^Ts} \end{align}\]

이제 $B \succ 0$일 때, $B^+ \succ 0$인지 살펴보면 다음과 같다 :

\[\begin{align} x^T B^+ x &= \left[\left(I -\frac{sy^T}{y^Ts} \right)x\right]^T B \left[\left(I -\frac{sy^T}{y^Ts} \right)x\right] + \frac{x^Tyy^Tx}{y^Ts} \nonumber \\ \\ & \left[\left(I -\frac{sy^T}{y^Ts} \right)x\right]^T B \left[\left(I -\frac{sy^T}{y^Ts} \right)x\right] > 0, \quad B \text{ is positive definite} \nonumber \\ & \frac{x^Tyy^Tx}{y^Ts} = \frac{(y^Tx)^2}{y^Ts} > 0, \text{as } y^Ts > 0 \text{ (Curvature Condition)} \nonumber \\ \nonumber \\ &\therefore x^T B^+ x > 0, \forall x \quad B^+ \text{ is positive definite} \end{align}\]

따라서 DFP는 $B$가 positive definite 임을 보장한다

단점

후술할 BFGS에 비해, 잘못 추정된 Hessian matrix를 바로잡는 속도가 느리다. $H$가 잘못 추정되어서 수렴 속도가 느려질 때 효과적으로 바로잡지 못한다.

반면 BFGS는 self-correcting property를 가지고 있어, 잘못된 추정을 몇 step 만에 도로 바로잡는다.

실전에서는 주로 BFGS가 사용되는 편이다.

BFGS(Broyden-Fletcher-Goldfarb-Shanno)

BFGS는 DFP와 비슷하지만, $B$와 $H$의 역할만 뒤바꾸면 된다.

BFGS(Broyden-Fletcher-Goldfarb-Shanno) update

\[\begin{align} B^+ &= B + \frac{yy^T}{y^Ts} - \frac{Bss^TB}{s^TBs} \label{bfgs-1} \end{align}\] \[\begin{align} H^+ = \left(I-\frac{sy^T}{y^Ts} \right) H \left(I-\frac{ys^T}{y^Ts}\right)+\frac{ss^T}{y^Ts}\label{bfgs-2} \end{align}\]

BFGS의 변형

L-BFGS(Limited-memory BFGS)는 BFGS의 메모리 사용량을 줄이기 위해 나온 방법이다. 밀도가 높은 $n \times n$크기의 행렬을 저장하는 대신, $n$차원의 벡터 몇개만 저장하여 근사한다.

참고1, 참고2

L-BFGS-B는 간단한 box constraint를 추가한 L-BFGS이다.

box constraint는 변수의 범위를 한정하는 제약조건으로, $a_i \leq x_i \leq b_i$ 같은 조건을 말한다.

참고