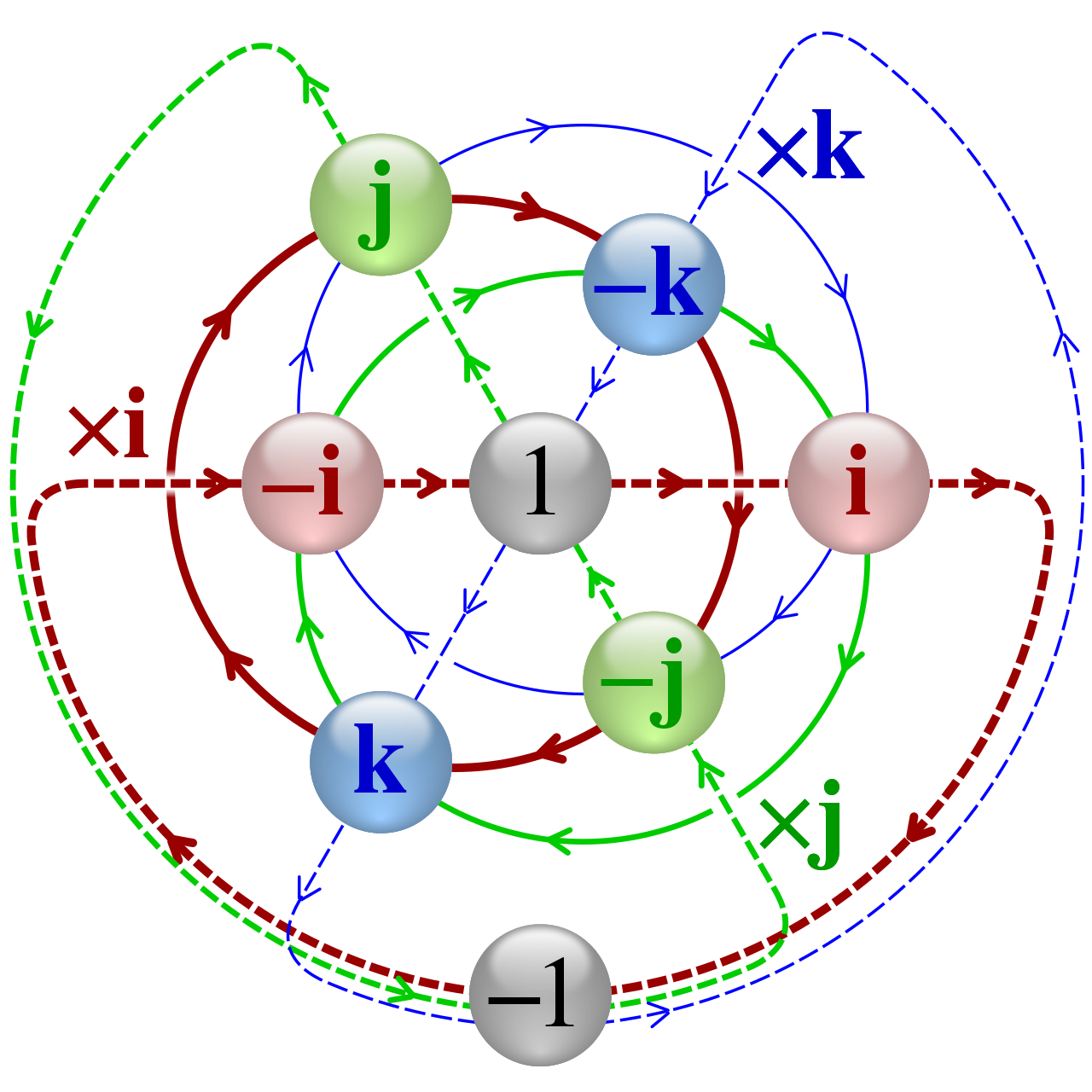
쿼터니언과 3차원 회전
사원수를 사용해서 어떻게 3차원 벡터를 회전할 수 있을까?
직전 포스트에서 다룬 쿼터니언 곱의 행렬 형태로부터 출발해 보자.
쿼터니안 곱의 행렬과 벡터 표현
임의의 두 쿼터니언 $q_1, q_2$에 있어서, 쿼터니언 곱의 행렬 표현은 다음과 같다.
\[\begin{align} q_1 \otimes q_2 &= [q_1]_\times q_2 \nonumber \\ \text{let } q \in \mathbb{H}, q &=w+xi+yj+zk \nonumber \\ [q]_\times &= \begin{bmatrix} w & -x & -y & -z \\ x & w & -z & y \\ y & z & w & -x \\ z & -y & x & w \end{bmatrix} \label{e1} \end{align}\]유도 과정은 복소수의 확장, 사원수(Quaternion)#쿼터니언-곱의-행렬-표현를 참고하자.
저 행렬을 다음과 같이 분해해보면, 뭔가 익숙한 형태들이 보이기 시작한다.
\[\begin{align} [q]_\times &=wI +\left[\begin{array}{c|ccc} 0 & -x & -y & -z \\ \hline x & 0 & -z & y \\ y & z & 0 & -x \\ z & -y & x & 0 \end{array}\right] \nonumber \\[10pt] &= wI + \left[\begin{array}{c|c} 0 & -v^T \\ \hline v & [v]_\times \end{array}\right] \label{e2} \\ \nonumber \\ v&=\begin{bmatrix}x & y & z\end{bmatrix}^T, \nonumber \\ [v]_\times &: \text{cross product matrix} \nonumber \end{align}\]뜬금없이 외적 행렬이 튀어나온다.
위에서 유도한 벡터 형태의 행렬 방식으로 쿼터니언의 곱을 벡터로 표현하면 다음과 같다
\[\begin{align} q_n&=w_n + \vec{v_n}, \nonumber \\[7pt] \vec{v_n} &= x_ni+y_nj+z_nk \nonumber \\[7pt] &= \begin{bmatrix} x & y & z \end{bmatrix}^T \nonumber \\[7pt] \nonumber \\ q_1 \otimes q_2 &= \left[w_1I+\begin{bmatrix}0 & -v_1^T \\ v_1 & [v_1]_\times\end{bmatrix}\right] \begin{bmatrix} w_2 \\ v_2 \end{bmatrix} \nonumber \\[8pt] &=\begin{bmatrix}w_1 w_2 \\ w_1 v_2\end{bmatrix} + \begin{bmatrix} -v_1^T \cdot v_2 \\ w_2 v_1 + [v_1]_\times v_2\end{bmatrix} \nonumber \\[8pt] &= \begin{bmatrix} w_1 w_2 - v_1^T v_2 \\ w_1 v_2 + w_2 v_1 + [v_1]_\times v_2\end{bmatrix} \label{e3} \\[8pt] &= (w_1 w_2 - \vec{v_1} \cdot \vec{v_2}) + (w_1 \vec{v_2} + w_2\vec{v_1} + \vec{v_1}\times\vec{v_2}) \label{e4} \end{align}\]
식 $\eqref{e3}$은 행렬 형태, $\eqref{e4}$는 벡터 형태이다.
이제 쿼터니언 곱의 교환법칙이 왜 성립하지 않는지 더 확실히 보인다. 결과의 벡터부에 있는 벡터의 외적 연산이 교환법칙이 성립하지 않기 때문이다.
즉, $\vec{v_1} \times \vec{v_2} \neq \vec{v_2} \times \vec{v_1}$이기 때문에 쿼터니언 역시 곱의 교환법칙이 성립하지 않는다.
더 재밌는건 여기부터 인데,
여기서 $q_1, q_2$이 pure quaternion 일 경우 다음과 같다.
실수부에는 벡터의 내적만, 허수부에는 벡터의 외적만 남았다.
참 신기한 일이 아닐 수 없다.
여담이지만, 벡터의 외적은 0,1,3,7차원 벡터에 대해서만 정의되며, 실수, 복소수와 초복소수(hypercomplex number)들과 관련이 있다.
쿼터니언의 Exponential
복소수의 exponential은 그 유명한 오일러 등식, $e^{i\theta}=\cos{\theta}+i\sin{\theta}$이다.
포스트 복소수의 Exponential Form과 극형식에서 테일러 급수를 사용하여 유도했었다.
그렇다면, 쿼터니언도 역시 ‘수’ 인데, exponential을 정의할 수 있지 않을까?
다시 당시 사용했던 테일러 급수 3개를 가져와 보자
\[\begin{align} e^{x} &= 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots \label{e_ex} \\ \sin{x} &= \frac{x}{1!} - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \label{e_sin} \\ \cos{x} &= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots \label{e_cos} \\ \text{Converge at }\forall x \nonumber \end{align}\]일단 $q=w+\vec{v}$를 바로 지수로 올려보면, $e^{q}$가 된다.
이는 $e^{w} e^{\vec{v}}$로 분리할 수 있으므로, 우리의 관심사는 $e^{\vec{v}}$가 어떤 형태가 될 것인지가 된다.
위에서 유도한 쿼터니안 곱의 벡터 형태를 참고해서 ($\eqref{e5}$) pure quaternion, $\vec{v}$의 거듭제곱들을 살펴보자.
\[\begin{align} \vec{v} &= \vec{v} \nonumber \\[5pt] \vec{v}^2 &= \begin{bmatrix}0 \\ \vec{v}\end{bmatrix} \otimes \begin{bmatrix}0 \\ \vec{v} \end{bmatrix} = \begin{bmatrix}-\vec{v}\cdot\vec{v} \\ \vec{v}\times \vec{v}\end{bmatrix} \\[5pt] &= \begin{bmatrix} -\lVert \vec{v} \rVert^2 \\ 0 \end{bmatrix} = -\lVert \vec{v} \rVert^2 : \text{scalar} \nonumber \\[5pt] \vec{v}^3 &= \vec{v}^2 \otimes \vec{v} = -\lVert \vec{v} \rVert^2 \vec{v} \nonumber \\[5pt] \vec{v}^4 &= \vec{v}^3 \otimes \vec{v} = -\lVert \vec{v} \rVert^2(\vec{v} \otimes \vec{v}) \nonumber \\[5pt] &= (-\lVert\vec{v} \rVert^2)^2 = \lVert \vec{v} \rVert^4 \nonumber \\[5pt] \vdots \nonumber \\ \end{align}\]뭔가 계속 순환하는 듯한 느낌이 든다.
이제 직접 $e^x$의 급수, $\eqref{e_ex}$에 대입해서 정리하면 다음과 같다.
마지막으로, $\vec{v} = \theta\vec{u}, \lVert \vec{u} \rVert=1$의 형태로 정리하면 드디어 형태가 나오게 된다.
따라서 사원수(Quaternion)의 Exponential은 다음과 같이 정리된다.
\[\begin{align} \text{pure quaternion, }q&=0+xi+yj+zk = 0+\vec{v} \nonumber \\ \vec{v} &= \theta \vec{u}, \lVert \vec{u} \rVert=1, \nonumber \\ \therefore e^{\vec{v}} = e^{\theta \vec{u}} &= \cos{\theta} + \vec{u} \sin{\theta}, \label{e8} \\ \end{align}\]
이게 재미있는 사실은, 복소수 때처럼 저 형태를 가진 모든 쿼터니언들의 크기가 1이라는 점이다.
\[\begin{align} \lVert e^{\theta \vec{u}} \rVert &= \lVert \cos{\theta} + \vec{u}\sin{\theta} \rVert \nonumber \\ &= \sqrt{\cos^2{\theta} + \sin^2{\theta}(u_x^2+u_y^2+u_z^2)} \nonumber \\ &= \sqrt{\cos^2{\theta} + \sin^2{\theta}(1)} = \sqrt{1} = 1 \nonumber \\ \end{align}\]따라서, 길이가 1인 모든 쿼터니안들은 $e^{\theta \vec{u}}$의 형태로 표현될 수 있다.
쿼터니언으로 3차원 벡터 회전
드디어 3차원 벡터를 회전시켜 볼 시간이다.
하지만 그전에 앞서, exponential form의 몇가지 성질을 알아야 한다.
Exponential form의 몇가지 성질들
임의의 단위 벡터(또는 pure quaternion), $\vec{u}$에 대해서, 각각 수직하고 평행인 벡터를 $\vec{u_\bot}, \vec{u_\parallel}$이라 하자.
이때 $e^{\theta\vec{u}}$은 pure quternion, $\vec{u_\bot}, \vec{u_\parallel}$과 몇가지 재미있는 성질을 가진다.
\[\begin{align} \vec{u} : \text{unit vector} \nonumber \\ \vec{u_\bot} \bot \vec{u}, \vec{u_\parallel} \parallel \vec{u} \label{e9} \\ \end{align}\]
- $\overline{e^{\theta\vec{u}}} = e^{- \theta\vec{u}}$
- $e^{\theta_1\vec{u}} e^{\theta_2\vec{u}} = e^{(\theta_1 + \theta_2)\vec{u}}$
- $e^{\theta\vec{u}} \otimes \vec{v_\parallel} = \vec{v_\parallel} \otimes e^{\theta\vec{u}}$ (commutative)
- $e^{\theta\vec{u}} \otimes \vec{v_\bot} = \vec{v_\bot} \otimes e^{-\theta\vec{u}}$ (non-commutative, but available with conjugate)
순서대로 증명해 보자.
- $\overline{e^{\theta\vec{u}}} = e^{- \theta\vec{u}}$
- $e^{\theta_1\vec{u}} e^{\theta_2\vec{u}} = e^{(\theta_1 + \theta_2)\vec{u}}$
- $e^{\theta\vec{u}} \otimes \vec{v_\parallel} = \vec{v_\parallel} \otimes e^{\theta\vec{u}}$ (commutative)
- $e^{\theta\vec{u}} \otimes \vec{v_\bot} = \vec{v_\bot} \otimes e^{-\theta\vec{u}}$ (non-commutative, but available with conjugate)
눈썰미가 좋은 사람이라면, 지금까지의 증명 과정에서 익숙한 부분들이 보였을 것이다.
$\vec{u_\bot}, \vec{u_\parallel}$ 등의 벡터를 3차원 회전변환 어딘가에서 본 기억이 난다.
드러나는 로드리게스 회전
로드리게스 회전은 원점을 지나는 임의의 축 $\vec{u}$에 대해서 $\theta$만큼 벡터$\vec{v}$를 회전시키는 공식이다.
이 공식은 이전 포스트들 중, 로드리게스 회전(Rodrigues rotation)에서 유도했다. 잘 기억이 나지 않는다면, 다시 읽어보길 권장한다.
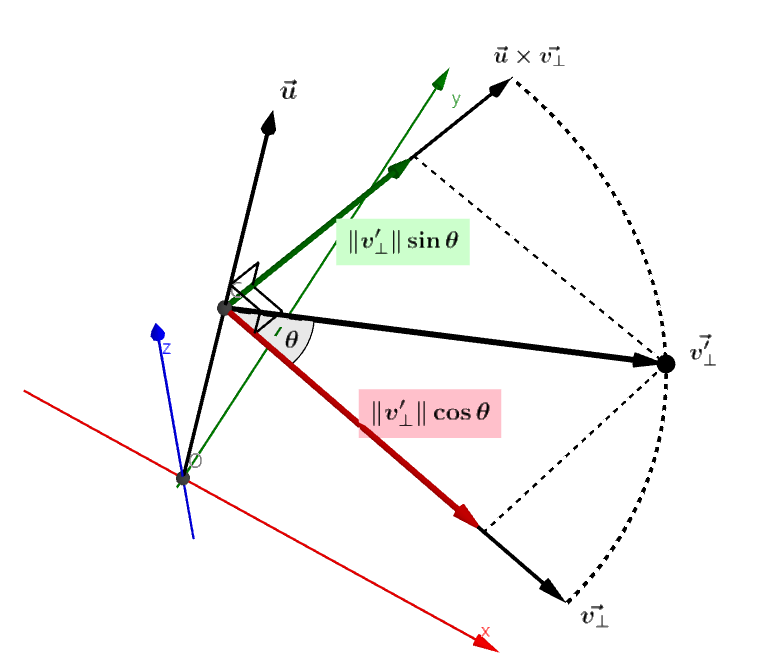
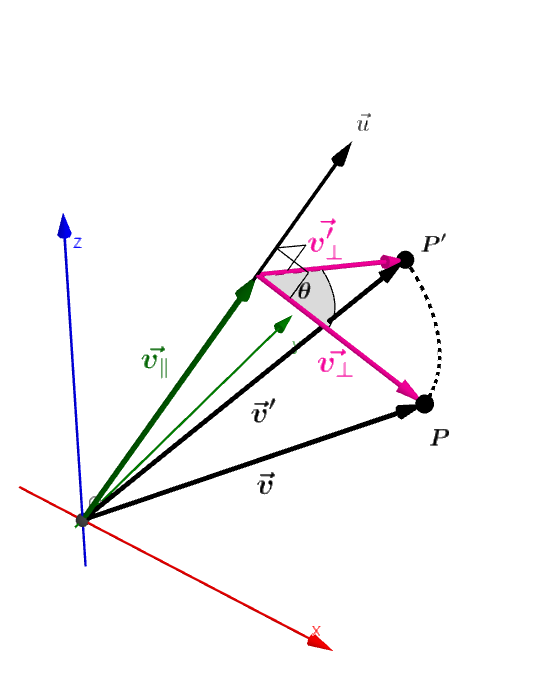그림 1: 회전축에 대해 평행과 수직 성분으로 분해된 벡터
그림 2: 수직 성분을 $\theta$만큼 회전시키기
그림1,2를 보자. 임의의 축 $\vec{u}$에 대해서 벡터 $\vec{v}$의 성분을 $\vec{v_\parallel} + \vec{v_\bot}$으로 분해할 수 있다.
이떄, $\theta$만큼 회전된 벡터 $\vec{v’}$는 다음과 같다.
자세한 내용은 이 포스트에서 확인할 수 있다.
그런데, 저 식 $\eqref{e11}$과 똑같은 형태가 쿼터니언의 exponential에 대한 성질들을 증명하는 도중에 등장했었다.
식 $\eqref{e10}$의 증명 과정 도중, pure quaternion의 형태에, 벡터 부분의 결과값이 완전히 동일하다.
즉, 쿼터니언의 Exponential과 수직한 벡터 $\vec{v_\bot}$의 쿼터니언곱은 다음과 같다
\[\begin{align} e^{\theta\vec{u}}\otimes \vec{v_\bot}&=\begin{bmatrix}0 \\ \cos{\theta}\vec{v_\bot} + \sin{\theta}\left(\vec{u} \times \vec{v_\bot}\right) \end{bmatrix} \\ &= \vec{v_\bot'} : \theta\text{ rotated vector around } \vec{u} \text{ axis} \end{align}\]슬슬 느낌이 온다.
3차원 벡터의 회전
임의의 회전축 $\vec{u}$로 각도 $\theta$만큼 벡터 $\vec{v}$를 회전시켜 보자. 이때 $\lVert \vec{u} \rVert = 1$이다.
우리가 원하는 것은 기존의 로드리게스 회전에서 처럼, $\vec{v} => \vec{v_\parallel} + \vec{v_\bot’}$으로 변환하는 것이다.
일단 무작정 곱해보자.
\[\begin{align} e^{\theta\vec{u}}\otimes \vec{v} &= e^{\theta\vec{u}}\otimes \vec{v}\\ &= e^{\theta\vec{u}}\otimes\vec{v_\parallel} + e^{\theta\vec{u}}\otimes\vec{v_\bot} \nonumber \\ &= e^{\theta\vec{u}}\otimes\vec{v_\parallel} +\vec{v_\bot'} \nonumber \end{align}\]$\vec{v_\parallel}$이 이상하게 변환돼서 돌아오지 못한다. 심지어 저 결과는 pure quaternion도 아니다.
그렇다면, 이렇게는 어떨까? 위에서 보였던 exponential의 성질들을 사용하자. $\eqref{e9}$
\[\begin{align} e^{\theta\vec{u}} \otimes \vec{v} \otimes e^{-\theta\vec{u}} &= e^{\theta\vec{u}} \otimes \left(\vec{v_\parallel} + \vec{v_\bot}\right) \otimes e^{-\theta\vec{u}} \nonumber \\ &= \left(e^{\theta\vec{u}} \otimes \vec{v_\parallel} \otimes e^{-\theta\vec{u}}\right) + \left( e^{\theta\vec{u}} \otimes \vec{v_\bot} \otimes e^{-\theta\vec{u}}\right) \nonumber \\ &= \left(e^{\theta\vec{u}} \otimes e^{-\theta\vec{u}} \otimes \vec{v_\parallel}\right) + \left( e^{\theta\vec{u}} \otimes e^{\theta\vec{u}} \otimes \vec{v_\bot} \right) \nonumber \\ &= e^{0}\otimes \vec{v_\parallel} + e^{2\theta\vec{u}}\otimes \vec{v_\bot} \\ &= \vec{v_\parallel} + \vec{v_\bot''} \nonumber \\ \vec{v_\bot''} : \text{rotate } \vec{v_\bot} \text{ by }2\theta \nonumber \end{align}\]성공적으로 $\vec{v_\parallel}$은 보존시켰지만, 이번에는 $\vec{v_\bot}$ 이 $2\theta$나 돌아가버렸다.
그렇다면, 처음부터 각도를 절반으로 줄여서, $e^{\frac{1}{2}\theta\vec{u}}$로 해본다면?
따라서, 3차원 벡터의 회전과 쿼터니안의 관계는 다음과 같다.
\[\begin{align} \text{let }\vec{v}, \vec{u} &\in \mathbb{R}^3, \nonumber \\ \vec{u} &: \text{rotating axis, } \lVert \vec{u} \rVert = 1, \nonumber \\ \theta &: \text{rotation angle} \nonumber \\ \nonumber \\ \text{attitude quaternion, }q &= e^{\normalsize \frac{\theta}{2}\vec{u}} \nonumber \\ &= \cos{\frac{\theta}{2}} + \vec{u}\sin{\frac{\theta}{2}} \label{e12} \\ \nonumber \\ \text{rotated vector, } \vec{v'} &= q \otimes \begin{bmatrix}0 \\ \vec{v}\end{bmatrix} \otimes \bar{q} \nonumber \\ &= q v \bar{q} \label{e13} \end{align}\]
이때 주의할 점은, $\frac{1}{2}\theta$ 이기 때문에, $[0, 4\pi]$의 범위를 가진다는 것이다.
\[\begin{align} q \neq -q, \text{ but}, \nonumber \\ \vec{v'} &= q \otimes \vec{v} \otimes \bar{q} \nonumber \\ &= (-q) \otimes \vec{v} \otimes \overline{(-q)} \end{align}\]
따라서 표현하는 3차원 자세는 동일하지만, 부호가 서로 다른 2개의 자세 쿼터니안이 존재하며, 다음과 같다.
따라서, 실제로 쿼터니언을 적용하여 제어할 때, 실수부 $w$의 부호를 항상 양수로 만들어 준다. 만약 $w<0$이면 전체에 -1을 곱한다. 이것을 canonicalize라고 한다. 하나의 자세를 나타내는 쿼터니언을 한 종류만 남겨놓는 것이다.
그렇지 않으면 나타내는 자세는 동일해도, 쿼터니언의 값이 달라짐에 따라서 자세의 차이를 나타내는 쿼터니언들의 값도 달라지는 등, 여러 문제가 생길 수 있다.
쿼터니언 회전 변환의 합성
기존의 3차원 회전 행렬 $R$을 다시 떠올려보자.
어떤식으로던, 회전 행렬 $R$을 사용한 회전 변환의 합성은 다음의 형태를 띄게 될 것이다.
\[\begin{align} \vec{a},\vec{b} &\in \mathbb{R}^3, \nonumber\\ \nonumber \\ R_{1} \vec{a} &=R_{2} \vec{b} \nonumber\\ R_2^T R_1 \vec{a} = R_{ab}\vec{a} &= \vec{b} \nonumber \\ \therefore R_{ab} = R_2^T R_1 \end{align}\]이 경우를 쿼터니언을 사용한 회전과 비교해 보자
\[\begin{align} q_1 \otimes \vec{a} \otimes \overline{q_1} = q_2 \otimes \vec{b} \otimes \overline{q_2} \nonumber \\ \overline{q_2} \otimes q_1 \otimes \vec{a} \otimes \overline{q_1} \otimes q_2 = \vec{b} \nonumber \\ => \left(\overline{q_2} \otimes q_1\right) \otimes \vec{a} \otimes \overline{\left(\overline{q_2} \otimes q_1\right)} = \vec{b} \nonumber \\ => q_{ab} \otimes \vec{a} \otimes \overline{q_{ab}} = \vec{b} \nonumber \\ \therefore q_{ab} = \overline{q_2} \otimes q_1 \end{align}\]재미있게도, 회전 행렬 처럼 회전의 합성이 동일한 방식으로 가능하므로, 기존의 회전 행렬을 사용해서 표현했던 두 자세간의 차이도 똑같이 표현된다.
자세의 차이에 대한 포스트에서 회전 행렬로 했던 것을, 그대로 쿼터니언으로도 가능하다는 뜻이다.
예를 들어, 기준계 $I$에 대해서 현재 비행체의 자세를 나타낸 쿼터니언을 $q_b$라 하고. 목표 자세를 $q_d$라 하자.
비행체의 좌표계 기준으로, 현재 자세에서 목표 자세로 가려면, 비행체가 앞으로 움직여야 하는 자세 쿼터니언은 다음과 같다.
\[\begin{align} q_{err} &= \overline{q_b} \otimes q_d=e^{\normalsize \theta\vec{u_B}} \nonumber \\ \vec{u_B} &: \text{rotation axis represented in Body frame} \nonumber \end{align}\]
쿼터니언을 사용한 많은 자세 제어 논문에서는 이 방식으로 desired 자세와 현재 자세에 대한 error 자세값을 구한다. PID 제어의 경우, $q_{err}$의 벡터 부분의 크기에 비례하고, 벡터의 방향으로 목표 각속도 벡터를 만드는 경우가 많다. 차피 관심있는 벡터는 Body Frame에서 관찰한 타겟 각속도 벡터, body rate이기 때문.
반대 방향의 곱인 $q_{diff} = q_2 \otimes \overline{q_1}$ 은 쿼터니언이 할 수 있는 자세의 자연스러운 전환 및 보간 방식인, 구면 보간(Spherical linear interpolation, SLERP) 에서 사용된다.
다음 포스트에서는 쿼터니언과 회전행렬, 그리고 미분된 쿼터니언과 각속도 벡터와의 관계에 대해 포스팅하겠다.