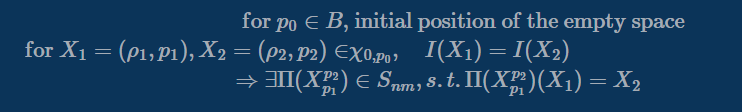슬라이딩 퍼즐의 도달 가능성(문제 정의)

슬라이딩 퍼즐의 도달 가능성에 대해 알아보기 전에, 이 포스트에서 다룰 문제를 명확히 정의하고자 한다.

앞서서 슬라이딩 퍼즐의 불변량에, 군과 대칭군의 여러 성질들을 알아보았지만, 아직까지도 슬라이딩 퍼즐의 도달 가능성에 대해서는 명확히 정의하지 않았다. 왜냐하면 퍼즐 자체에 대한 여러가지 정의가 모호했기 때문이다.

예를 들어서 퍼즐을 푸는 경로 라고 하면, 조각을 바꾸는 변환인지? 아니면 단순한 빈칸 좌표의 나열인지?
인접한 타일이란 무엇이며, 타일에 번호를 부여한다는 것은 무엇인지?
슬라이딩 퍼즐의 현재 상태를 어떻게 정의하고, 상태들 간의 변환은 어떻게 정의하는지? 등등의 여러가지 의문점이 있다.

이번 포스트에서는 슬라이딩 퍼즐의 도달 가능성 문제와 관련된 다양한 개념들을 명확히 정의하고, 이후 포스트에서 이 문제를 해결하는 방법을 포스팅 할 것이다.

거의 모든 정의를 새로 내려야 하므로 다소 길고 지루하겠지만, 수학적으로 빈틈없이 정의하는 것이 중요하므로 어쩔 수 없다.

대신 한번 정의가 끝나면 이후 포스트에서는 오로지 식과 문자만으로 문제를 다룰 수 있게 될 것이다.

정의

2D 슬라이딩 퍼즐의 가로가 $m$칸, 세로가 $n$칸이라고 하자.

정의 1 : 인덱스 집합

이 퍼즐의 각 칸의 좌표의 집합 $B$를 다음과 같이 정의한다.

인덱스 집합(Index Set), B

\[\begin{align} \text{for } a \in \mathbb{N}, [a] &:= \{n \in \mathbb{N} \mid 1 \leq n \leq a\} \\ \text{for } m, n \in \mathbb{N}, \text{Index Set } B_{n, m} &:= [n] \times [m] \\ &= \{(a,b) \mid a \in [n], b \in [m]\} \\ \end{align}\]

우리는 가로 세로가 각각 $m, n$칸인 슬라이딩 퍼즐만 다룰 것이므로, 이후부터 $B$는 $B_{n, m}$을 의미한다고 하자.

정의 2 : 평탄화 함수

주어진 2D 슬라이딩 퍼즐의 좌표를 1D 배열의 인덱스로 바꾸는 평탄화 함수 (flattening function), $\phi$를 다음과 같이 정의한다 :

평탄화 함수(Flattening Function), $\phi$

\[\begin{align} \text{for } (a,b) \in B, \quad \phi &: B \to [nm] \\ &:= (a,b) \mapsto m(a-1) + b \\ \nonumber \\ \phi \text{ is bijective} \quad \phi^{-1} &: [nm] \to B \\ &:= k \mapsto \left(\left\lceil \frac{k}{m} \right\rceil, \; ((k-1) \bmod m) + 1 \right) \\ \end{align}\]

그냥 가로가 $m$칸인 2D 배열을 1D 배열로 쭉 펴는 것과 같다. 각각의 인덱스의 시작 번호가 1부터 시작한다는 점에 유의하자.

정의 3 : 슬라이딩 퍼즐의 순열

슬라이딩 퍼즐의 조각들에 대한 순열 $\sigma$를 다음과 같이 정의한다 :

슬라이딩 퍼즐의 순열 $\sigma$ \(\begin{align} \sigma \in S_{nm} \text{ acts on } [nm], B \\ \text{for } k \in [nm], \quad \sigma &: [nm] \to [nm] \\ &:= k \mapsto \sigma(k) \\ \text{for } p \in B, \quad \sigma &: B \to B \\ &:= p \mapsto \phi^{-1} \circ \sigma \circ \phi (p) \\ \end{align}\)

군의 작용(Group Action)이 등장했는데, 다음과 같다 :

군의 작용(Group Action)

\[\begin{align} &\text{for a group } G \text{ and a set } X, \\ &\text{a group action } \alpha : G \times X \to X \\ &\text{must satisfy :} \\ \text{1. } &\text{for } x \in X, \quad \alpha(e, x) = x, \text{ where } e \text{ is the identity element of } G \\ \text{2. } &\text{for } g, h \in G, x \in X, \quad \alpha(g \cdot h, x) = \alpha(g, \alpha(h, x)) \\ \end{align}\]

더 자세한 정의는 다음을 참고하자 :
Group Action(Wiki)

먼저 $S_{nm}$이 1D 인덱스 집합 $[nm]$에 작용하는 것은 자명하다.
다음으로 2D 좌표 집합 $B$에 작용하는 것은, 평탄화 함수 $\phi$가 bijective이므로 여전히 군의 작용의 조건을 만족한다.

또한 지금은 $\sigma \in S_{nm}$가 $[nm], B$에만 작용하지만, 추후 퍼즐의 상태 공간, $\chi$에 대한 작용(Action)까지도 확장할 것이다.

정의 4 : 슬라이딩 퍼즐의 상태공간

슬라이딩 퍼즐의 현재 상태 $X$와 초기 상태 $X_0$를 다음과 같이 정의한다 :

슬라이딩 퍼즐의 상태, $X$

\[\begin{align} X &= (\sigma, p) \\ \sigma &\in S_{nm} \text{ is the permutation of the pieces} \\ p=(a,b) &\in B \text{ is the coordinate of the empty space} \\ \end{align}\]

즉 슬라이딩 퍼즐의 현재 상태는
1) 조각들이 어떻게 섞였는지 나타내는 순열 $\sigma$와,
2) 빈칸의 현재 좌표 $p=(a,b)$로 정의된다.

슬라이딩 퍼즐의 초기 상태, $X_0$

\[\begin{align} X_0 &= (e, p_0) \\ e &\text{ is the identity permutation in } S_{nm} \\ p_0=(a_0,b_0) &\text{ is the initial coordinate of the empty space} \\ \end{align}\]

초기 상태는 당연하게도 조각들을 섞지 않는 항등순열 $e$와, 빈칸의 초기 좌표 $p_0=(a_0,b_0)$로 정의된다.

슬라이딩 퍼즐의 상태공간, $\chi$

\[\begin{align} \chi &= \{(\sigma, p) \mid \sigma \in S_{nm}, p \in B \} \\ \end{align}\]

슬라이딩 퍼즐의 상태공간 $\chi$는 가능한 모든 슬라이딩 퍼즐의 상태 $X=(\sigma, p)$의 집합으로 정의된다.

이제 슬라이딩 퍼즐의 상태공간 $\chi$의 부분집합 $\chi_k \subset \chi$를 다음과 같이 정의한다 :

빈칸의 위치가 $p$인 부분집합, $\chi_p$

\[\begin{align} \text{for } p \in B, \quad \chi_p &:= \{ (\sigma, k) \in \chi \mid k = p \} \\ \end{align}\]

또 다른 부분집합, $\chi_{0,p} \subset \chi$를 다음과 같이 정의한다 :

초기 빈칸의 위치가 $p$인 부분집합, $\chi_{0,p}$

\[\begin{align} \text{for } p \in B, \quad \chi_{0,p} &:= \{(\sigma, k) \in \chi \mid \sigma^{-1}(k) = p\} \end{align}\]

정의 5 : 순열의 상태공간에 대한 작용

슬라이딩 퍼즐의 상태공간 $\chi$에 대한 순열 $\sigma \in S_{nm}$의 작용(action)을 다음과 같이 정의한다 :

순열의 상태공간에 대한 작용, $\sigma$

\[\begin{align} \text{for } \sigma, \rho \in S_{nm}, \quad \sigma &: \chi \to \chi \\ &:= (\rho, p) \mapsto (\sigma \cdot \rho, \sigma(p)) \\ \end{align}\]

이는 $S_{nm}$이 각각 자기 자신과, $B$에 작용하는 것을 합친 것이므로, 군의 작용이 된다.
이 작용은 순열이 기존의 조각을 섞는 순열과 합성되고, 동시에 빈칸도 같이 움직임을 표시하는 것이다.

정의 6 : 인접 관계와 인접 집합

슬라이딩 퍼즐에서 어떠한 두 칸의 인접함을 다음과 같이 정의하자 :

인접 관계(Adjacency Relation), $\sim$

\[\begin{align} \text{for } p_1=(a_1, b_1), p_2=(a_2, b_2) \in B, \quad \\ p_1 \sim p_2 \iff \lvert a_1-a_2 \rvert + \lvert b_1-b_2 \rvert = 1 \end{align}\]

현재 칸 기준으로 상하좌우 한 칸씩 떨어진 칸이 인접한 칸이다. 물론 인덱스 셋의 범위를 벗어나면 안 된다.

인접 집합(Adjacency Set), $N(p)$

\[\begin{align} \text{for } p \in B, \quad N(p) &= \{p' \in B \mid p' \sim p\} \\ \end{align}\]

칸 $p$에 인접한 칸들의 집합을 $N(p)$로 정의했다. 이 집합은 슬라이딩 퍼즐에서 빈 칸이 이동할 수 있는 다음 위치에 대한 집합이다.

정의 7 : 원자적 움직임

슬라이딩 퍼즐에서 빈칸을 한 칸 이동시키는 원자적 움직임(atomic move)를 다음과 같이 정의하자 :

원자적 움직임(Atomic Move), $\tau_u^{v}$

\[\begin{align} \text{for } u, v \in B, &\quad u \sim v \\ \text{Let } &\tau_{uv}\in S_{nm} \text{ be the transposition swapping } \phi(u),\phi(v).\\ \tau_u^v &: \chi_u \to \chi_v,\qquad \tau_u^v(\sigma, u) := (\tau_u^v\cdot \sigma,\; v) \\ \end{align}\]

일반적인 transposition과 크게 다를 바 없어 보이나, 기존 $\chi$에 대한 작용의 정의역과 공역을 각각 $\chi_u, \chi_v$로 제한하였다는게 중요하다.

즉, 빈칸이 $u$에서 $v$로 이동하는 원자적 움직임은, 빈칸의 위치를 $u$에서 $v$로 바꾸고, 빈칸과 $v$에 있던 조각을 맞바꾸는 transposition $\tau$를 슬라이딩 보드 상태 순열에 곱하는 것이다.

이 원자적 움직임은 빈칸이 제자리에 있지 않은 나머지 보드 상태들에 대해서는 정의되지 않는다.
이를 이용하면, 경로와 움직임을 명시적으로 정의할 수 있다.

정의 8 : 경로와 움직임

슬라이딩 퍼즐에서 빈칸이 여러 칸을 이동하는 경로를 다음과 같이 정의하자 :

경로(Path), $P_u^{v}$

\[\begin{align} \text{for } u, v \in B, \\ P_u^{v} &:= (\tau_u^{u_1}, \tau_{u_1}^{u_2}, \ldots, \tau_{u_{k-1}}^{u_k}, \tau_{u_k}^{v}), \text{where } k \geq 0 \\ \nonumber \\ \mathbb{P}_u^v &:= \{P_{u'}^{v'} \mid u' = u, v' = v\} \\ &:= \text{ the set of all paths from } u \text{ to } v \\ \end{align}\]

경로는 빈칸을 연달아 움직이는 원자적 움직임들의 나열로써 정의한다.

이제 다음과 같이, 빈칸을 $u$에서 $v$로 움직이는 움직임(Move)을 정의하자 :

움직임(Move), $\Pi_u^{v}$

\[\begin{align} \text{for } u, v \in B, \\ \Pi(P_u^{v}) &:= \tau_{u_k}^{v} \cdot \tau_{u_{k-1}}^{u_k} \ldots \cdot \tau_{u_1}^{u_2} \cdot \tau_u^{u_1} \\ &: \chi_{u} \subset \chi \to \chi_{v} \subset \chi \\ &\text{acting on limited domain, codomain of } \chi, \\ \nonumber \\ \text{where }& \Pi(P_u^{v}) \in S_{nm} \\ \text{ is the }&\text{composition of the transpositions in } P_u^{v} \\ \end{align}\]

Remark: 슬라이딩 퍼즐의 불변량

앞서 포스트에서 정의한 슬라이딩 퍼즐의 불변량 $I$를 위 정의에 맞춰 다시 쓰면 다음과 같다 :

슬라이딩 퍼즐의 불변량, $I(X)$

\[\begin{align} \text{for } X \in \chi, \quad I(X) &: \chi \to \{-1, +1\} \\ &:= \sigma, (a,b) \mapsto \text{sgn}(\sigma) \cdot (-1)^{a+b} \\ \end{align}\]

초기 불변량도 $I_0 = I(X_0)$으로 간단하게 정의된다.

이제 원래의 불변량 명제도 다음과 같이 쓸 수 있다 :

슬라이딩 퍼즐의 불변량 명제

\[\begin{align} \text{for }& p_0 \in B, \text{ initial position of the empty space} \\ \text{for }& X_0=(e, p_0), X=(\rho, p) \in \chi_{0, p_0}, \\ &I(X_0) \neq I(X) \Rightarrow \nexists P_{p_0}^{p} \in \mathbb{P}_{p_0}^{p}\ \text{s.t.}\ \Pi(P_{p_0}^{p})(X_0) = X. \\ \end{align}\]

즉, 시작 빈칸의 위치가 동일한 상태들 사이에서, 불변량이 다른 두 슬라이딩 퍼즐의 상태 $X_0, X$가 있을 때, $X_0$에서 $X$로 변환할 수 있는 슬라이딩 퍼즐의 움직임(Move)은 존재하지 않는다는 것이다.

슬라이딩 퍼즐의 도달 가능성 명제

이제 슬라이딩 퍼즐의 도달 가능성 명제를 다음과 같이 정의하자 :

슬라이딩 퍼즐의 도달 가능성(Reachability) 명제

\[\begin{align} \text{for }& p_0 \in B, \text{ initial position of the empty space} \\ \text{for }& X_1=(\rho_1, p_1), X_2=(\rho_2, p_2) \in \chi_{0, p_0}, \\ &I(X_1) = I(X_2) \Rightarrow \exists P_{p_1}^{p_2} \in \mathbb{P}_{p_1}^{p_2}\ \text{s.t.}\ \Pi(P_{p_1}^{p_2})(X_1) = X_2. \\ \end{align}\]

시작 빈칸의 위치가 동일하고, 불변량이 같은 임의의 두 슬라이딩 퍼즐의 상태 $X_1, X_2$가 있을 때,
항상 $X_1$에서 $X_2$로 변환할 수 있는 슬라이딩 퍼즐의 움직임(Move)이 존재함을 보이는 것이다.

자세히 보면, 불변량 명제와 정확히 역 명제 관계에 있음을 알 수 있다.
즉, 두 명제를 전부 증명하면 우리가 기대하는 가해 가능성에 대한 정리를 얻을 수 있을 것이다.

마치며

정의만 잔뜩 늘어놓으니 읽는 사람 입장에선 되게 재미없고 지루했을 것이다.

하지만 나는 마음속에서 직관적으로 이해하고 있던 개념들을 수학적으로 엄밀하게 정의해 보는 작업을 통해 여러가지 수학 표기법과 정의를 쌓아올리는 연습을 할 수 있었다.

결과적으로 나한테만 좋은 포스트다.

어쨌거나 이제 슬라이딩 퍼즐의 도달 가능성 문제에 대한 모든 정의가 끝났다. 다음 포스트에서 드디어 도달 가능성 문제를 증명할 것이다.
정의가 기억나지 않는다면, 다시 이 포스트로 돌아와서 확인하면 된다.