슬라이딩 퍼즐은 항상 풀릴까?
슬라이딩 퍼즐 조각을 흩었다가 아무렇게나 다시 조립했을 때, 그 슬라이딩 퍼즐을 풀 수 있을 확률이 어떻게 될까?
서론
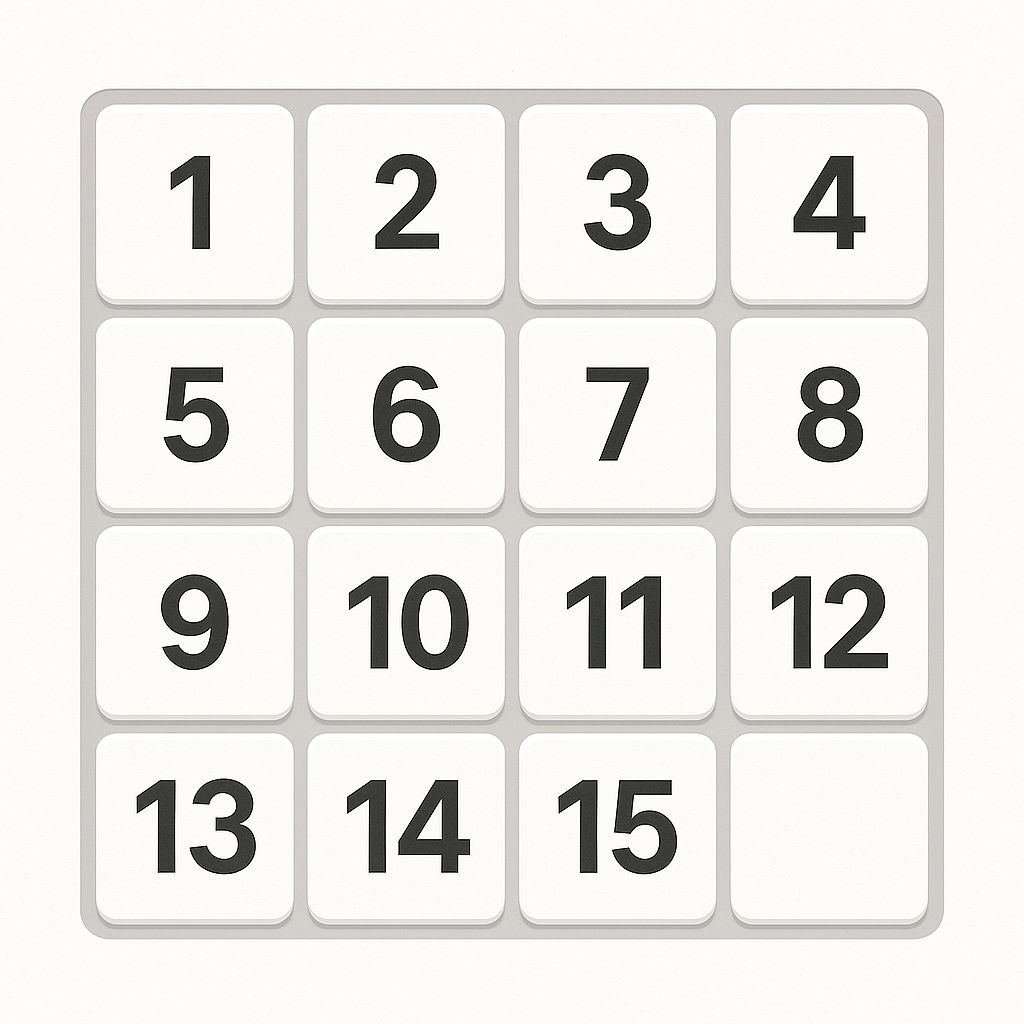
슬라이딩 퍼즐을 모르는 사람은 없다.
원래의 이미지를 각 칸으로 나누고, 빈칸을 하나 남겨서 그 빈칸을 이리저리 슬라이드 시켜가며 맞추는 간단한 퍼즐.
이 퍼즐을 맞추는 방법은 널리 알려져 있고, 각각의 조각의 원래 위치가 어디인지 안다면 더더욱 쉽게 풀 수 있다.
아무 생각 없이 사이트 하나에 들어가 4x4 슬라이딩 퍼즐을 맞추다가, 문득 한가지 궁금증이 생겼다.
슬라이딩 퍼즐은 조각이 아무렇게나 섞여있어도 반드시 맞출 수 있을까?
슬라이딩 퍼즐의 해결 가능성
나는 곧바로 온라인 4x4 슬라이딩 퍼즐 사이트에서 불가능한 경우가 있는지 시도해 보았다.
그런데 생각 외로 굉장히 단순한 반례가 있었다.
14<->15번 조각만 바꿨을 뿐인데, 갑자기 사이트에서 풀 수 없는 퍼즐이라는 경고가 뜬 것이다.
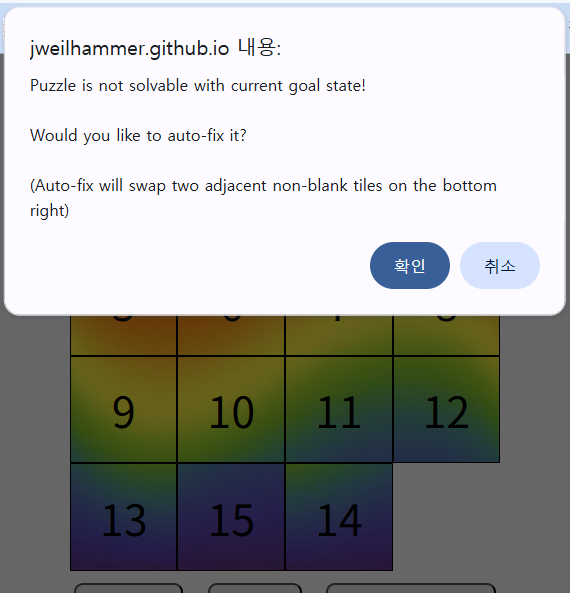 그림 3 : 14<->15 교환만 했는데도 풀 수 없는 퍼즐이라니
그림 3 : 14<->15 교환만 했는데도 풀 수 없는 퍼즐이라니
어이없게도 첫번째 시도 만에 바로 반례를 찾은것도 황당했는데, 더 황당한 건 이것을 solvable(해결 가능)로 만드는 방법이었다.
그냥 맨 아래의 아무 두 조각을 교환하기만 해도 다시 solvable이 된다고?
이후 해당 사이트에서 shuffle을 눌러 아무렇게나 퍼즐을 섞은 뒤, 다양하게 조각들을 교환한 다음 unsolvable(해결 불가능) 경고가 뜨는지 확인했다.
그 결과 다음 성질들을 예측해 볼 수 있었다.
- 아무 두 조각이나 교환하면 solvable을 unsolvable로 만들 수 있는 것 같다.
- 아무 두 조각이나 교환하면 unsolvable을 solvable로 만들 수 있는 것 같다.
그 말인즉, 슬라이딩 퍼즐을 바닥에 쏟아버린 뒤 아무렇게나 조각을 끼워 넣은 다음, 내가 아무 두 조각을 교환할 때마다 solvable과 unsolvable 상태 사이를 진동한다는 뜻이 된다.
이 가설이 사실이라면, 역으로 슬라이딩 퍼즐이 맞춰진 시점으로부터 교환을 짝수번 한 모든 상태가 solvable, 홀수번 한 모든 상태는 unsolvable이 된다는 걸까?
나는 이 시점에서 추가적인 궁금증이 생겼다.
첫번째로,
조각을 짝수번 교환해서 만들 수 있는 모든 상태는 전부 solvable인가?
혹시나 짝수번 교환해서 만들 수 있는 상태인데, solvable이 아닐 수도 있지 않을까?
두번째로,
모든 solvable 상태는 전부 조각을 짝수번 교환해서 만들 수 있는가?
혹시나 solvable 상태인데 짝수번 교환으로 만들 수 없는 경우가 있는지?
세번째로,
바닥에 슬라이딩 퍼즐을 쏟아버린 다음 아무렇게나 조각을 끼워 넣었을 때,
그게 solvable 일 확률은 어떻게 될까?
마지막으로,
애초에 내가 세운 짝수 교환에 따른 해결 가능성 가설은 진실일까?
군론과 대칭성
이 문제를 체계적이고 수학적으로 접근하기 위해서는 군론(Group Theory)이 필요하다.
군론은 대칭성(Symmetry)을 연구하는 수학의 한 분야이다.
대칭성이라고 해서 뭔가 거창해 보이지만, 결국 어떠한 대상의 구조를 보존하는 일련의 변환(Transformation)들을 모아놓은 것이다.
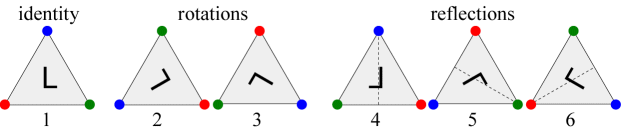
예를 들어, 정삼각형은 0도, 120도, 240도 회전과 좌우 대칭을 포함한 6가지의 대칭을 유지하는 변환들을 가진다.
재미있는 건, 이 변환들이 서로 합성(Composition)될 수 있다는 점이다.
예를 들어, 120도 회전과 좌우 대칭을 합성하면 240도 회전이 된다.
또한, 120도 회전을 3번 합성하면 원래 상태로 돌아온다.
즉 이를 수식으로 표현하면 다음과 같다.
\[R_{120} \circ \left(R_{120} \circ R_{120}\right) = e\]여기서 $R_{120}$은 120도 회전을 의미하고, $e$는 아무것도 안하는 변환, 즉 항등 변환(Identity Transformation)을 의미한다.
슬라이딩 퍼즐을 대칭성으로 바라보기
이제 슬라이딩 퍼즐의 대칭성에 대해 생각해 보자.
16번 빈칸에서 출발해 빈칸을 이리저리 움직여 다시 16번이 빈칸으로 돌아오는 모든 행동의 집합을 생각해 보자.
\[G = \{e, g_1, g_2, g_3, ... \}\]여기서 각 $g_i$는 빈칸을 이리저리 움직이는 하나의 행동을 의미한다.
예를 들어, $g_1$은 빈칸을 시계방향으로 한바퀴 돌려 제자리로 돌아오는 행동일 수 있다.
또 다른 예로는, $g_2$는 빈칸을 2x3 영역 안에서 한바퀴 돌려 제자리로 돌아오는 행동일 수 있다.
이러한 행동들은 서로 합성될 수 있는데, 각각의 행동을 한 결과에 다시 다른 행동을 적용하는 것이다.
예를 들어 $g_1$을 먼저 하고 그 다음에 $g_2$를 하는 행동은, 먼저 $g_1$ 행동을 그대로 퍼즐에 적용한 다음, 그 결과에 $g_2$ 행동을 적용하는 것이다.
그리고 이렇게 합성된 새로운 행동 역시 어쨌든 빈칸을 이리저리 움직였다가 다시 16번이 빈칸으로 돌아오는 행동이므로, 여전히 집합 G에 속한다.
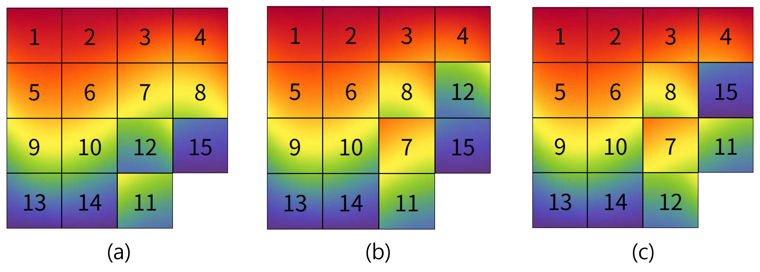 그림 5 : 슬라이딩 퍼즐의 합성. (a)가 $g_1$, (b)가 $g_2$, (c)가 $g_2 \circ g_1$을 의미한다.
그림 5 : 슬라이딩 퍼즐의 합성. (a)가 $g_1$, (b)가 $g_2$, (c)가 $g_2 \circ g_1$을 의미한다.
이를 수식으로 나타내면 다음과 같다 :
\[g_2 \circ g_1 \in G\]다음으로, 빈칸을 16번에 고정하고, 나머지 조각들이 아무렇게나 움직이는 행동의 집합을 생각해 보자.
\[H = \{e, h_1, h_2, h_3, ... \}\]여기서 각 $h_i$는 빈칸을 16번에 고정한 채, 나머지 조각들이 아무렇게나 움직이는 하나의 행동을 의미한다. 예를 들어, $h_1$은 1번 조각과 2번 조각을 교환하는 행동일 수 있다. 또 다른 예로는, $h_2$는 1번 조각, 2번 조각, 3번 조각을 시계방향으로 한 칸씩 회전시키는 행동일 수 있다.
이러한 행동들도 서로 합성될 수 있으며, 16번 빈칸은 애초에 건드리질 않으므로 여전히 집합 H에 속한다. 이를 수식으로 나타내면 다음과 같다 :
\[h_2 \circ h_1 \in H\]이제 재미있는 점은, $G$의 모든 행동이 $H$ 안에 포함된다는 것이다.
왜냐하면, 빈칸을 이리저리 움직이는 행동은 결국 빈칸을 16번에 고정한 채 나머지 조각들을 움직이는 행동이기 때문이다.
즉 $G$는 $H$의 부분집합이다 :
\[G \subseteq H\]그런데, $H$가 1~15번 조각들을 아무렇게나 배치하는 모든 행동의 집합이라면, 이건 우리가 이미 알고 있는 대상이 된다. 고등학교 때 배운, 15개의 원소를 나열하는 경우의 수 15! 이다.
그렇다면 $H$와 $G$의 관계를 살펴보면 앞의 4가지 궁금증에 대한 답을 얻을 수 있을까?
결론
물론 가능하다.
하지만 그러기 위해서는 $H$가 정확히 어떤 집합인지,
그 구조와 성질이 무엇인지 알아야 한다.
그나마 다행인 것은, $H$가 이미 잘 알려진 구조라는 점이다.
바로 군론에서의 대칭군(Symmetric Group), $S_{15}$이다.
결국 우리는 군론(Group Theory)을 공부하고, $H$의 구조를 파악해야 한다. 하지만 그 과정에서 $G$의 구조도 자연스럽게 알게 될 것이며, 생각지도 못한 결과를 얻게 될지도 모른다.
이번 시리즈는 내가 처음으로 추상적인 수학을 공부하는 과정의 기록이기도 하다.
직관을 중심으로 내린 결론이 과연 맞는지를 한없이 추상적으로 증명하는 과정이 될 것이다.
하지만 이 추상성은 오히려 직관을 더 명확하게 해주기도 하며, 완전히 새로운 관점을 제공해 주기도 한다.
나는 슬라이딩 퍼즐의 해결 가능성이라는 문제가 그 대표적 예라고 생각한다.
다음 포스팅부터 군론의 기초 개념과 그에 따른 기본 성질들을 살펴보겠다.