대칭군(Symmetric Group)
대칭군이란 무엇이고, 왜 이렇게 중요하게 다뤄질까?
참고 1 : https://en.wikipedia.org/wiki/Symmetric_group
참고 2 : https://dec41.user.srcf.net/notes/IA_M/groups.pdf
대칭군이란
대칭군(Symmetric group)란, 주어진 집합의 모든 순열(permutation)로 구성된 군을 말한다.
즉, 집합의 원소들을 서로 바꾸는 모든 방법을 고려한 군이다.
대칭군은 보통 $S_n$으로 표기하며, 이는 $n$개의 원소를 가진 집합의 대칭군을 의미한다.
예를 들어, $S_3$는 3개의 원소를 가진 집합의 모든 순열로 이루어진 군이다.
물론 이건 어디까지나 유한 집합의 대칭군에 대한 이야기이며, 무한 집합의 대칭군도 존재한다.
‘대칭’ 이라는 단어의 체급에서 느껴지듯이, 대칭군은 군론에서 매우 중요한 역할을 한다.
사실상 모든 군들의 아버지격인 존재라고 할 수 있는데,
이는 바로 다음에 소개할 케일리 정리(Cayley’s theorem) 때문이다.
순열로써의 대칭군
먼저 이해하기 쉽게 유한한 대칭군에 대한 직관적 접근인 순열로써의 대칭군을 소개하겠다.
유한 대칭군 (순열 버전)
어떤 유한 집합 $X$의 모든 순열(permutation)로 구성된 군을 유한 대칭군이라고 한다.
즉, $X$의 원소들을 서로 바꾸는 모든 방법을 고려한 군이다.
이 군을 $S_n$ (만약 $X$의 원소 개수가 $n$개라면)으로 표기한다.
쉽게 말해, $n$개의 원소를 가진 집합이 있을 때, 그 원소들을 서로 바꾸는 모든 방법을 모아놓은 군이 바로 $S_n$이다.
고등학교의 순열과 조합 때 배우는 바로 그 순열이 여기서 말하는 순열이며, 어렵지 않게 $S_n$ 의 원소의 개수가 $n!$ (n 팩토리얼)임을 알 수 있다.
예를 들어, $S_3$는 3개의 원소를 나열하는 모든 방법을 모아놓은 군이며, 이렇게 표현할 수 있다 :
\[\begin{align} S_3 = \{ (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1) \} \end{align}\]여기서 각 원소 자체가 순열이자, 행동이 된다. 예를 들어 $(1,2,3)$은 1, 2, 3을 그대로 두는 행동이고, $(1,3,2)$는 2와 3을 서로 바꾸는 행동이다.
대칭군의 이항 연산은 순열의 합성이며, 예를 들면 :
\[\begin{align} (1,2,3) \cdot (1,3,2) = (1,3,2) \end{align}\]이 되는 식이다.
아주 당연하게도 교환법칙은 성립하지 않는다.
대칭군 원소의 표기법
대칭군의 원소를 표기하는 방법은 여러 가지가 있는데, 여기서는 두 가지 방법을 소개하겠다.
행렬 표기법 (Matrix Notation) :
\[\begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}\]
순열을 행렬 형태로 나타내는 방법이다.
예를 들어, $S_3$의 원소 $(1,3,2)$는 다음과 같이 표기할 수 있다 :이는 첫 번째 행이 원래의 위치를, 두 번째 행이 순열 후의 위치를 나타낸다.
예를 들어, 위의 순열을 $(a,b,c)$에 적용/작용(Action) 하면, $(a,b,c) \rightarrow (a,c,b)$가 된다.
사이클 표기법 (Cycle Notation) :
\[(1 \ 3 \ 2)\]
순열을 사이클 형태로 나타내는 방법이다.
예를 들어, 1이 3으로, 3이 2로, 2가 1으로 이동하는 사이클은 다음과 같다 :만약 어떤 원소가 자기 자신으로 이동한다면, 그 원소는 생략할 수 있다.
예를 들어, 아무것도 안하는 행동, $e$는 사이클 표기법으로는 그냥 $(1)(2)(3)$이지만, 보통은 생략하고 아무것도 쓰지 않는다.위 행렬 표기법의 순열을 싸이클 표기법으로 바꾸면, 다음과 같다 :
\[(3 \ 2)\]즉, 1은 건드리지 않고, 3이 2로, 2가 3으로 이동하는 사이클을 나타낸다.
행렬 표기법이 직관적이긴 하지만, 사이클 표기법이 더 간결하고 편리한 경우가 많고 사실상 주류이다.
따라서 이 글에서도 사이클 표기법을 주로 사용할 것이다.
싸이클 표기법으로 $S_3$의 원소들을 모두 쓰면 다음과 같다 :
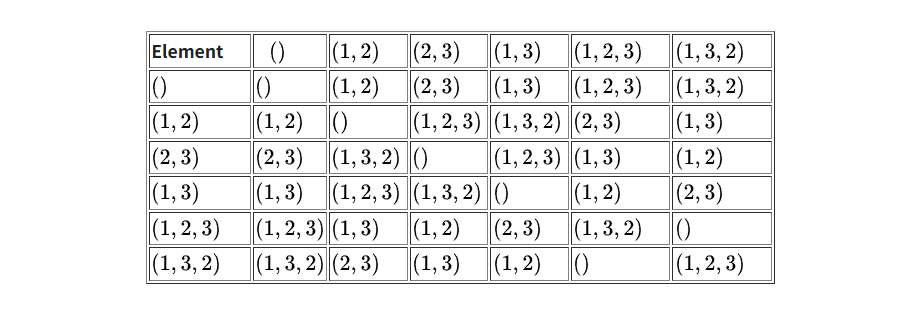
\[\begin{align} S_3 = \{ e, (1 \ 2), (1 \ 3), (2 \ 3), (1 \ 2 \ 3), (1 \ 3 \ 2) \} \end{align}\]여기서 $e$는 항등원(identity element)을 의미하며, 아무것도 하지 않는 행동이다.
이 표기법에서는 $(1 \ 2 \ 3)$이나 $(2 \ 3 \ 1)$이나 $(3 \ 1 \ 2)$나 모두 같은 순열을 의미한다는 점에 주의하자.
보통은 가장 작은 수부터 시작하는 표기법을 사용한다.
대칭군의 진짜 정의
그런데, 이러면 무한한 집합의 대칭군은 어떻게 정의할까?
유한할 때는 순열로써 정의할 수 있었지만, 무한할 때도 이 정의를 그대로 사용할 순 없다. 당장 정수 집합을 섞는 순열을 정의할 수 있을까? 정수를 섞는 모든 방법의 개수를 셀 순 없다. 무한대임은 자명하다.
무한 대칭으로 정의를 확장하려면, 우리는 ‘섞음’ 자체를 재정의할 필요가 있다.
이제 대칭군의 진짜 정의를 소개한다
대칭군 (Symmetric group)
어떤 집합 $X$에 대해, $X$에서 $X$로 가는 전단사 함수(bijective function)들의 집합을 대칭군이라고 한다.
이 군을 $Sym(X)$로 표기한다 :$Sym(X) = \{ \sigma : X \to X \mid \sigma \text{ is bijective function} \} $
위 정의에서 제일 중요한 단어는 바로 전단사 함수(bijective function)이다. 일대일 대응(one-to-one correspondence)함수라고도 부른다.
즉, 어떤 원소가 다른 원소로 정확히 하나씩 대응되는 함수이다.
따라서, 전단사 함수는 원래 집합의 모든 원소를 정확히 하나씩 다른 원소로 보내는 함수이다.
이는 우리가 ‘섞음’이라고 생각하는 것과 정확히 일치한다.
이 정의를 사용하면 어떠한 원소를 섞는 작용을 더 쉽게 표현할 수 있다 :
\[\begin{align} \sigma : X \to X \\ x \mapsto \sigma(x) \end{align}\]여기서 $\sigma(x)$는 $x$가 섞인 후의 위치를 의미한다.
두 원소의 합성도 다음과 같이 함수의 합성으로 쉽게 표현할 수 있다 :
\(\begin{align} (\sigma \cdot \tau)(x) = \sigma(\tau(x)) \end{align}\) 즉, $\tau$가 먼저 작용하고, 그 다음에 $\sigma$가 작용하는 것이다.
이를 통해 군의 원소의 표현과, 그 원소가 다른 집합의 원소에 영향을 미치는 작용(Action)을 명확히 구분할 수 있다.
여기서 잠시 전단사 함수에 대해 더 자세히 알아보자. 앞으로도 자주 등장할 개념이기 때문이다.
전사, 단사, 전단사
참고 1 : https://en.wikipedia.org/wiki/Injective_function
참고 2 : https://en.wikipedia.org/wiki/Surjective_function
참고 3 : https://en.wikipedia.org/wiki/Bijective_function
전단사 함수는 전사(Surjective)이면서 단사(Injective)인 함수이다.
각각의 정의부터 살펴보자
전사 함수 (Surjective function)
어떤 함수 $f : A \to B$에 대해,
임의의 $b \in B$에 대해, $f(a) = b$인 $a \in A$가 항상 존재한다.
이 함수가 공역의 모든 원소를 만들어 낼 수 있다는 뜻이다. 함수의 치역(image)과 공역(codomain)이 일치하는 함수로 이해해도 된다.
단사 함수 (Injective function)
어떤 함수 $f : A \to B$에 대해,
임의의 $a_1, a_2 \in A$에 대해, $f(a_1) = f(a_2)$이면, $a_1 = a_2$이며, 역도 성립한다.
즉, $a_1 = a_2 \Leftrightarrow f(a_1) = f(a_2)$ 이다.
이 함수가 서로 다른 원소를 서로 다른 원소로 보낸다는 뜻이다.
즉, 어떤 원소가 다른 원소로 정확히 하나씩 대응되는 함수이다.
서로 다른 두 원소가 같은 원소로 대응될 수 없으며, 서로 다른 원소는 반드시 서로 다른 공역의 원소로 대응된다.
이제 전단사 함수의 정의는 상대적으로 쉬워진다.
전단사 함수 (Bijective function)
어떤 함수 $f : A \to B$에 대해, $f$가 전사 함수이면서 단사 함수이면, $f$는 전단사 함수이다.
따라서, 전단사 함수는 원래 집합의 모든 원소를 정확히 하나씩 다른 원소로 보내는 함수이다.
쉽게는 일대일 대응 함수라고도 부르며, 이하 간단한 예시다.
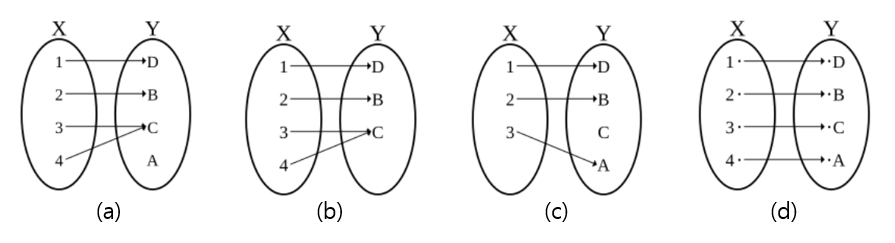그림 1 : (a) 아무것도 아닌 함수, (b) 전사, (c) 단사, (d)전단사
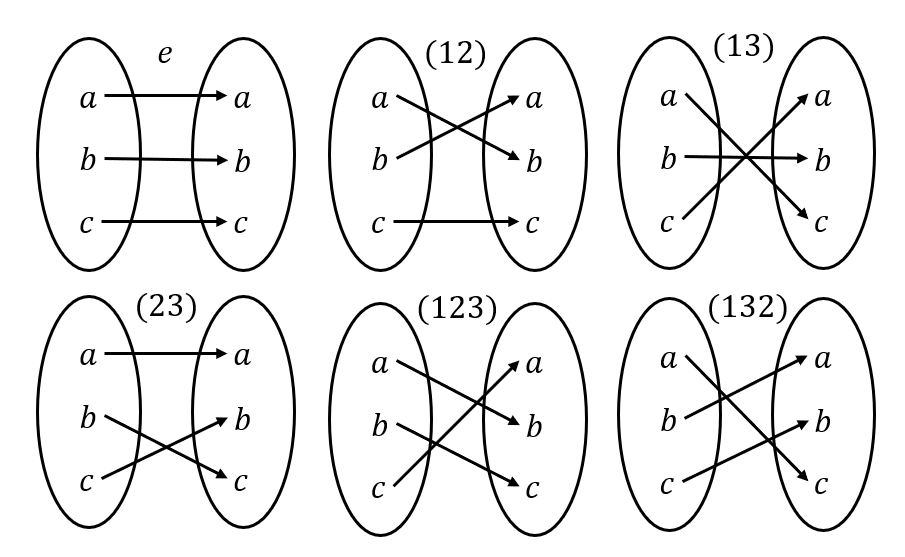
섞는 다는 것은, 어떤 원소를 정확히 다른 원소로 보내고, 모든 원소가 정확히 하나씩만 대응되는 변환이다. 즉, 섞음을 같은 집합 내에서의 전단사 함수로 정의할 수 있다.
예시로 앞의 $S_3$의 예시를 전단사 함수들로 다시 보이면 다음과 같다 :
그림 2 : S_3의 원소들을 전단사 함수로 표현하기
물론 유한 집합 뿐만 아니라, 무한 집합까지도 확장할 수 있는 더 일반적인 정의이다.
전단사 함수의 성질
대칭군이 전단사 함수들의 집합으로 정의되었으나, 왜 이 집합이 군을 이루는지는 아직 보이진 않았다.
다행히도, 전단사 함수는 아래의 성질들을 만족시키며, 이를 통해 전단사 함수들의 집합이 군을 이룸을 알 수 있다 :
항등원 (Identity element) :
모든 집합 $X$에 대해, 항등 함수 $id_X : X \to X$는 전단사 함수이다.
즉, $id_X(x) = x$ for all $x \in X$.역원 (Inverse element) :
만약 $\sigma : X \to X$가 전단사 함수라면, 그 역함수 $\sigma^{-1} : X \to X$도 전단사 함수가 된다.
즉, $\sigma(\sigma^{-1}(x)) = \sigma^{-1}(\sigma(x)) = x$ for all $x \in X$.합성 (Composition) :
만약 $\sigma, \tau : X \to X$가 전단사 함수라면, 그 합성 함수 $\sigma \circ \tau : X \to X$도 전단사 함수이다.
즉, $(\sigma \circ \tau)(x) = \sigma(\tau(x))$ for all $x \in X$.결합법칙 (Associativity) :
모든 집합 $X$에 대해, 전단사 함수의 합성은 결합법칙을 만족한다.
즉, 만약 $\sigma, \tau, \rho : X \to X$가 전단사 함수라면, $(\sigma \circ \tau) \circ \rho = \sigma \circ (\tau \circ \rho)$ for all $x \in X$.
따라서 집합인 $Sym(X)$는 군이 된다는 것을 알 수 있다.
여기에 또 하나의 재밌는 성질이 있는데,
바로 전단사 함수의 존재만으로도 정의역과 공역의 크기가 같음을 보장한다는 것이다.
즉, 만약 어떤 집합 $X$에 대해 전단사 함수 $\sigma : X \to Y$가 존재한다면, $X$의 원소의 개수는 $Y$의 원소의 개수와 같다. 이를 다음과 같이 쓸 수 있다 :
\[\begin{align} if \ there \ exists \ \sigma : X \to Y \ such \ that \ \sigma \ is \ bijective, \\ then |X| = |Y| \end{align}\]
이는 전단사 함수가 일대일 대응이기 때문에, 정의역의 원소와 공역의 원소가 정확히 일치해야 하기 때문이다.
만약 정의역의 원소보다 공역의 원소가 더 많다면, 어떤 원소는 대응되지 못하며,
반대로 정의역의 원소가 공역보다 더 많다면, 어떤 원소는 반드시 두 개 이상의 원소와 대응되어야 하기 때문이다.
따라서 두 집합의 크기가 같음을 보이려면, 그 두 집합 사이에 전단사 함수가 존재함을 보이면 된다.
이 논리가 라그랑주 정리(Lagrange’s theorem)를 비롯한 여러 군론 정리의 핵심 아이디어로 사용된다.
마치며
그 유명한 대칭군의 정의를 알아보았다.
눈치 챘겠지만, 슬라이딩 퍼즐의 군론적 접근 역시 이 대칭군의 개념을 주로 사용하게 될 것이다. 결국 퍼즐 조각을 섞는 다는 것 자체가, 바로 대칭군의 원소인 전단사 함수로써 표현될 수 있기 때문이다.
일례로, 맨 처음에 보였던 슬라이딩 퍼즐 움직임의 합성을 보자.
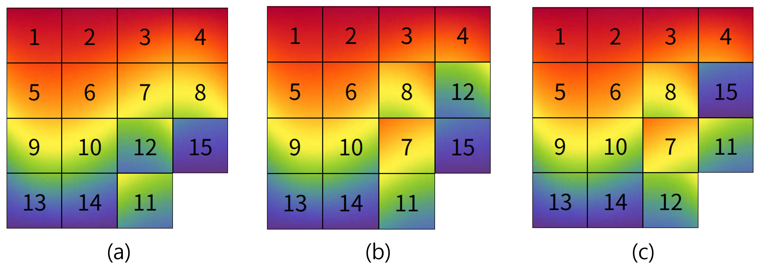그림 3 : (a) 시계방향으로 돌리기, (b) 3x2크기를 시계방향으로 돌리기, (c) (a)를 한다음 (b) 하기
슬라이딩 퍼즐 나머지 15개의 조각을 섞는 저 행동을 대칭군의 싸이클 표기로 하면 :
(a) : $(11 \ 15 \ 12)$
(b) : $(7 \ 11 \ 15 \ 12 \ 8)$
(c) = (b) $\circ$ (a) : $(7 \ 11 \ 12 \ 15 \ 8)$
이 된다.
슬라이딩 퍼즐이 조각을 섞는 방식이 곧 대칭군의 원소이므로, 대칭군에 대해 알아갈수록 슬라이딩 퍼즐의 구조에도 더 깊이 다가갈 수 있을 것이다.
다음으로 잠시 군론의 가장 중요한 정리 중 하나인 케일리 정리(Cayley’s theorem)를 소개하려고 한다.
케일리 정리(Cayley’s theorem)는 사실 슬라이딩 퍼즐과 직접적인 관련은 없다.
하지만 그 내용이 가히 충격적이고, 증명 과정도 굉장히 재밌어서 그냥 소개할 것이다.
관심이 없으면 다음 포스트는 넘어가도 된다.