벡터의 회전과 좌표계 변환의 관계
벡터의 회전 변환과 강체의 자세 표현은 어떤 관계가 있는가. 좌표계 간의 변환은 어떻게 이루어 지는가
앞선 포스트에서 평면상의 한 벡터를 원점에 대해 회전시키는 회전 변환(또는 회전 행렬)에 대해 다루었다.
그 형태는 다음과 같았다.
원점에 대해 $\theta$ 만큼 회전시키는 회전 변환 행렬 \(\begin{equation} \begin{bmatrix} \cos{\theta} && -\sin{\theta} \\ \sin{\theta} && \cos{\theta} \end{bmatrix} = R(\theta), \text{Rotation Matrix} \end{equation}\)
그렇다면, 점을 회전시키는 변환을 사용하여 어떻게 강체의 자세를 표현할 수 있을까?
벡터의 회전 변환과 강체의 자세 표현
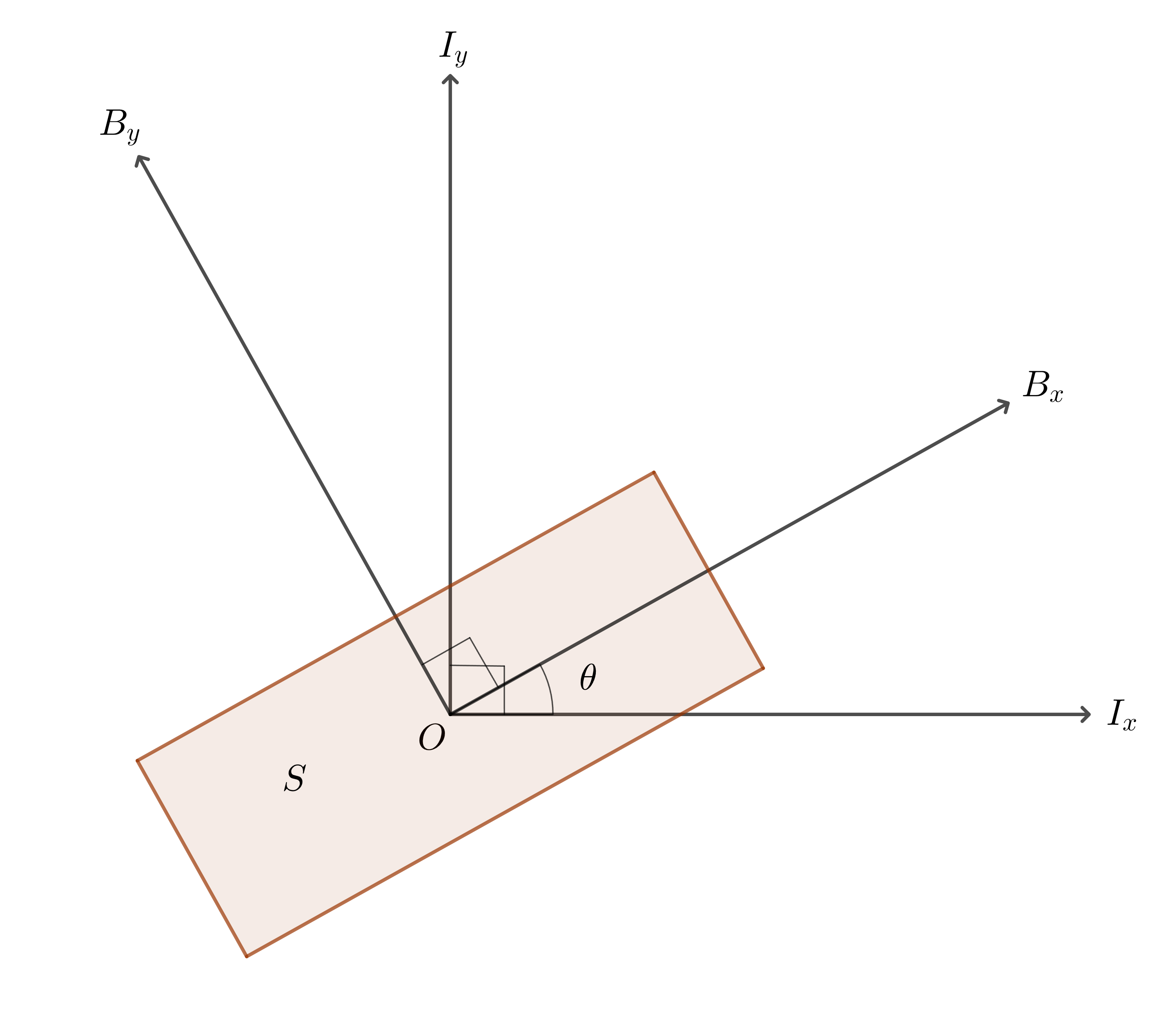
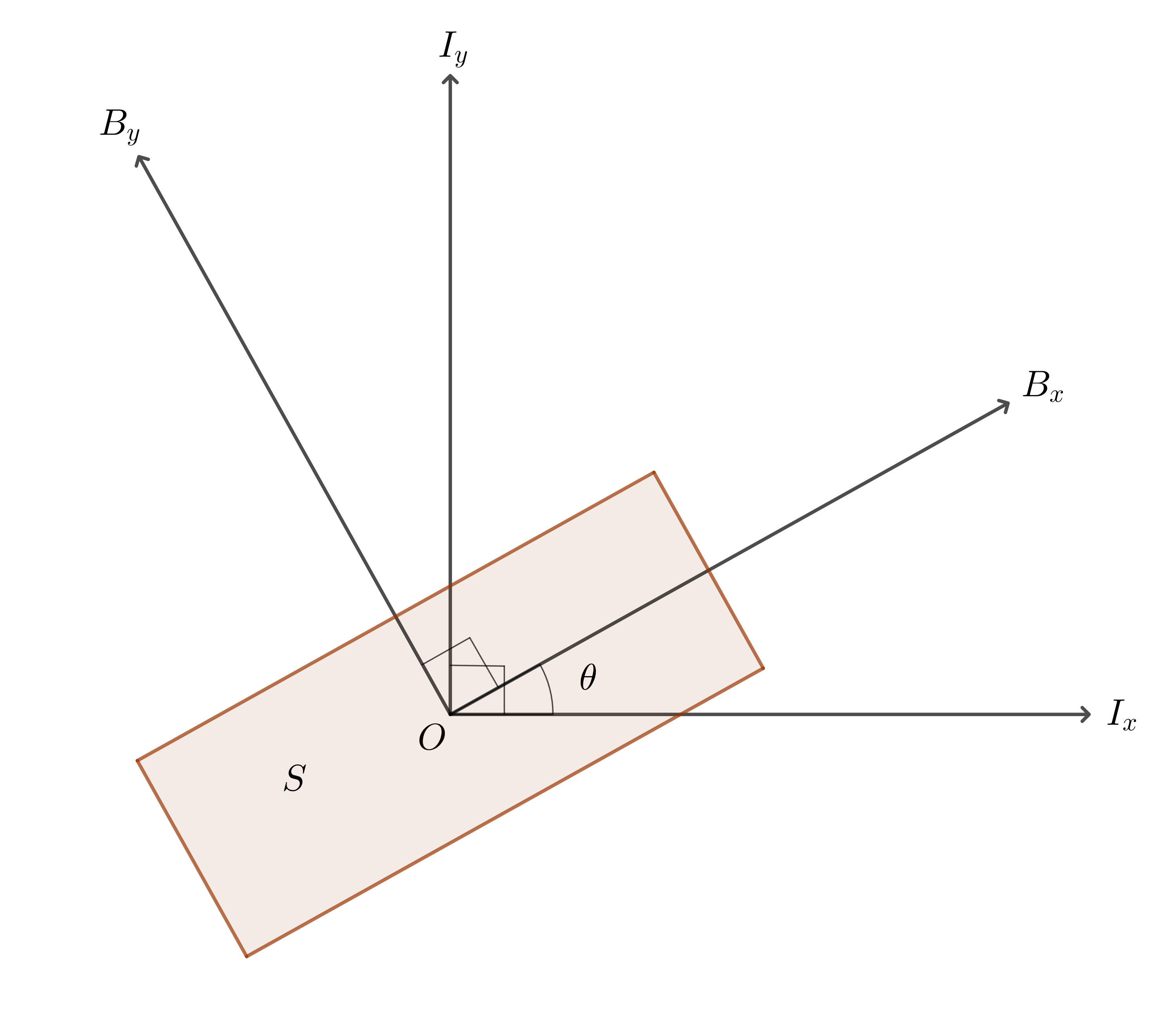그림 1 : $\theta$만큼 회전된 강체를 생각해보자
그림 1에서와 같이 2차원 상의 막대를 생각해보자. 이때, 막대와 같이 붙어서 움직이는 Body Frame($B$)을 생각해 볼 수 있다. 막대가 자세가 변함에 따라, 기준이 되는 Reference Frame(Inertial Frame, $I$)의 축 벡터와의 각도 역시 변할 것이다.
$I$ frame의 $x,y$방향 단위 축 벡터를 $i_x, i_y$, $B$ frame의 $x,y$방향 단위 축 벡터를 $b_x, b_y$ 하자. 따라서 $\left\Vert\vec{i_x}\right\Vert = \left\Vert\vec{i_y}\right\Vert = \left\Vert\vec{b_x}\right\Vert = \left\Vert\vec{b_x}\right\Vert = 1$이며, $\vec{i_x} \bot \vec{i_y}$, $\vec{b_x} \bot \vec{b_y}$ 이다.
이때, $i_x$ 벡터를 $\theta$ 만큼 원점에 대해 회전하면 $b_x$ 벡터가 된다. 물론 $y$ 축의 경우도 똑같다.
따라서 다음의 관계가 성립한다.
결국 각도 $\theta$ 하나만으로 기준 좌표계에 상대적인 강체의 Body Frame의 단위 축 벡터들을 결정할 수 있다.
2차원 상에서의 강체의 자세도 역시 scalar 값 하나, $\theta$로 표현할 수 있음을 의미하며, 이는 기준 좌표계의 좌표축에 대해 강체의 좌표축이 기울어진 정도와 같다.
좌표계의 회전 변환
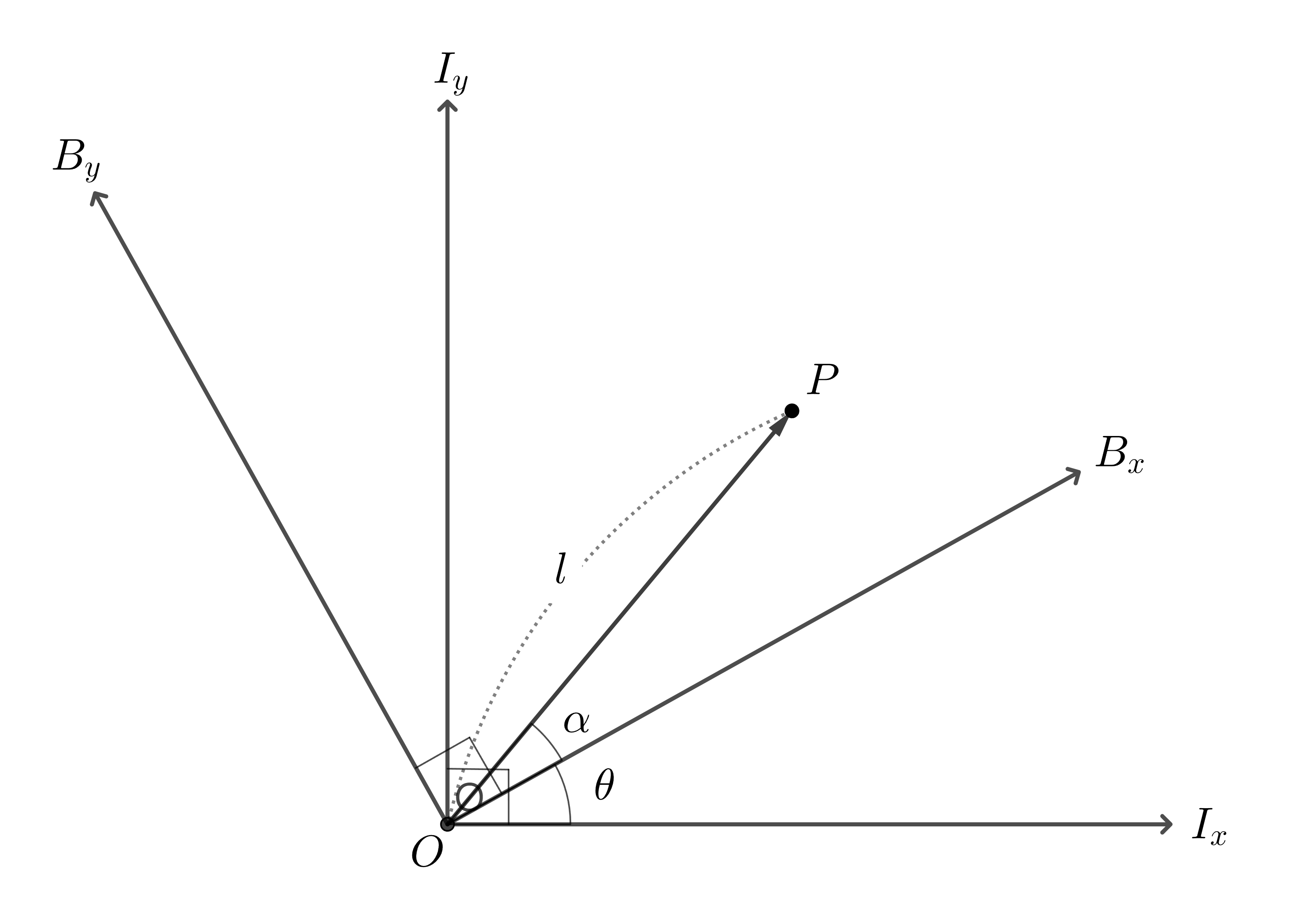그림 2 : 고정된 점을 표현하는 서로 다른 2개의 좌표계.
다음 그림 2를 보자.
그림2의 점 $P$는 평면상에 고정된 점이다. 하지만 이 점의 위치를 표현하는 방법은 무수히 많다. 그 중에서도 그림2 와 서로 다른 2개의 회전된 좌표계의 경우를 살펴보자.
하나는 기준 좌표계인 $I$, 다른 하나는 기준 좌표계에 대해 $\theta$ 만큼 회전된 좌표계 $B$이다. 이때, 각각의 좌표계 $I,B$에서 관찰한 점 $P$의 위치 벡터를 각각 $P_I, P_B$라 하자.
$I$ 좌표계의 입장에서 보면, 점 $P$는 길이가 $l$이고, 각도는 $\alpha + \theta$이다. 이는 극좌표 형식으로 다음과 같이 표현할 수 있다.
\[\begin{equation} P_I = l \begin{bmatrix} \cos{\alpha + \theta} \\ \sin{\alpha + \theta} \end{bmatrix} \label{e1}\end{equation}\]이번엔 $B$ 좌표계의 입장에서 보면, 점 $P$는 길이가 $l$이고 각도는 $\alpha$이다. 이는 극좌표 형식으로 다음과 같이 표현할 수 있다.
\[\begin{equation} P_B = l \begin{bmatrix} \cos{\alpha} \\ \sin{\alpha} \end{bmatrix} \label{e2}\end{equation}\]식 $\eqref{e1}$와 $\eqref{e2}$를 들여다 보면, $P_I$를 $-\theta$ 방향으로 회전 시킨 벡터가 $P_B$ 임을 알 수 있다. 즉, 다음 관계가 성립한다.
\[\begin{align} R(-\theta) P_I = P_B \label{e3}\\ => R(\theta)^{-1}P_I = P_B \\ => R(\theta) P_B = P_I \label{e4} \end{align}\]
그런데.. 뭔가 행렬의 형태와 결과가 뒤집힌 듯한 느낌이다.
벡터 회전 vs 좌표계 회전
식 $\eqref{e3}$, $\eqref{e4}$을 보면 이전의 벡터를 회전시킬때와는 사뭇 다른 방향으로 회전 행렬이 작용하는 것을 볼 수 있다.
이전 포스트에서 다뤘던 벡터의 회전을 생각해보자
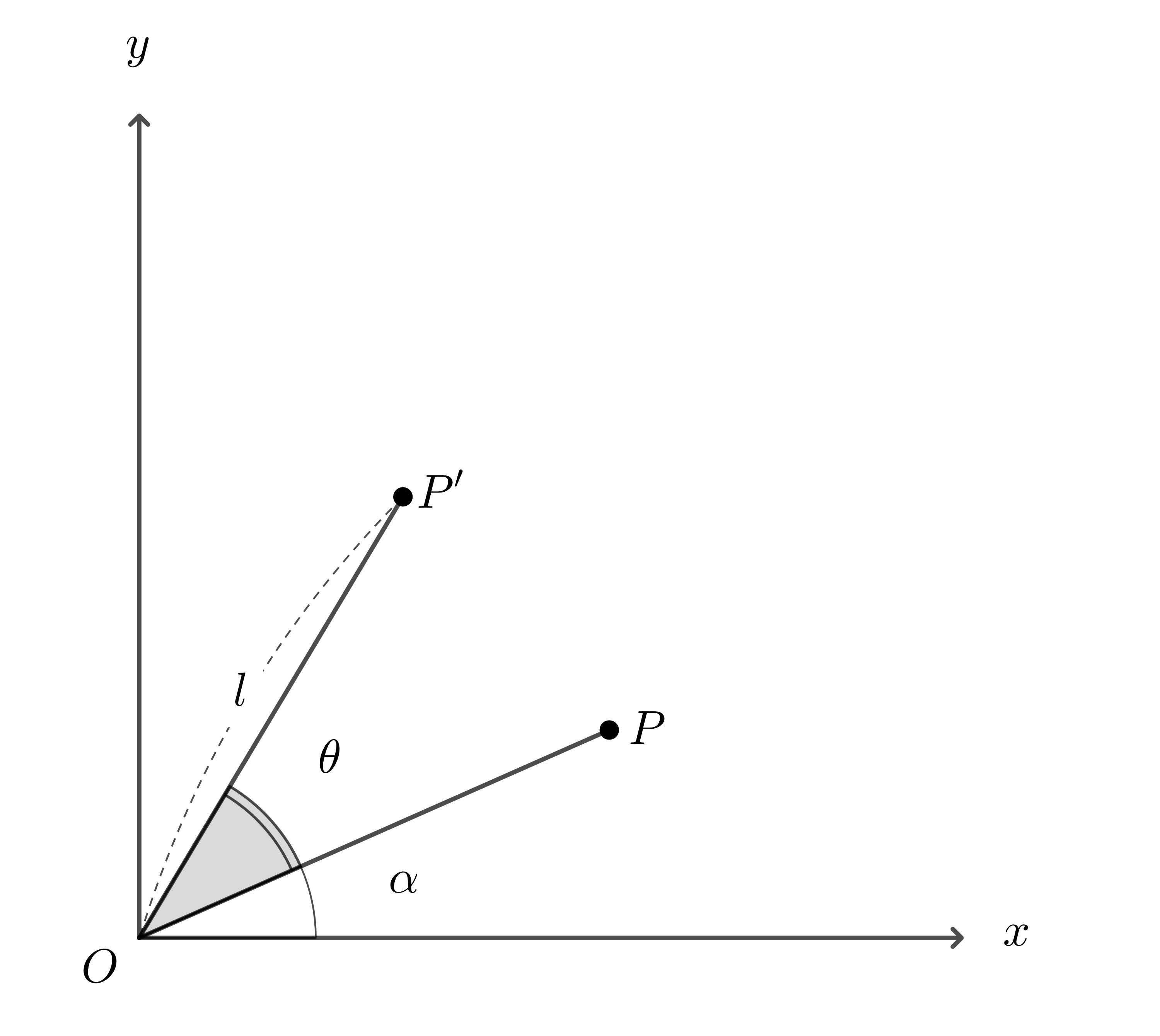그림 3 : $\theta$만큼 $P -> P’$로 회전시킨다.
평면상의 벡터를 회전시킬 때는, $R(\theta)$를 곱해서 점 $P->P’$로 회전시킨다. 어떻게 보면 정방향 처럼 생각할 수도 있겠다.
그런데 좌표계의 회전 변환을 할 땐, $R(-\theta)$를 곱해서 $P_I -> P_B$로 변환한다. 그렇다면 이것 역시 정방향인가?
회전 변환이 벡터의 회전변환인지, 좌표계의 회전 변환인지에 따라서 실제 회전 행렬의 값은 서로 정 반대가 된다.
다른 사람이 쓴 회전 행렬 $R(\theta)$가 당연히 벡터 회전 기준인 $\begin{bmatrix} cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{bmatrix}$ 인 줄 알고 읽었는데, 뭔가 이상해서 계산해보니 좌표계 회전 변환 기준인 $\begin{bmatrix} cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{bmatrix}$일 수 있는 것이다.
따라서, 회전 변환 이라 할때는 반드시 그것이 좌표계의 회전 변환인지, 또는 벡터의 회전 변환인지를 정확하게 해줘야 한다.
통상 회전 변환은 대개 벡터의 회전 변환을 이야기 하는 경우가 많다. 하지만 회전 변환의 관점에 따라 그 방향이 서로 반대가 됨 역시 기억해야 할 것이다.
이를 정리하면 다음과 같다.
벡터 회전 행렬, $R_{vec}(\theta) = \begin{bmatrix} cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{bmatrix}$,
(그림 3) $R_{vec}(\theta) P = P’$좌표계 회전 변환 행렬, $R_{frame}(\theta) = \begin{bmatrix} cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{bmatrix}$,
(그림 2) $R_{frame}(\theta) P_I = P_B$이떄, $R_{vec}(\theta)^{-1} = R_{vec}(\theta)^T=R_{vec}(-\theta) = R_{frame}(\theta)$
이 부분은 Rotation Matrix의 위키피디아의 “Ambiguities” 부분에도 소개되어 있다. 좌표계의 회전 변환 vs 벡터의 회전 변환. Alias vs Alibi. 또는 Passive vs Active Transformation 와 같은 다양한 명칭이 있다.
참고 : 영문 위키피디아 Rotation Matrix#Ambiguities, Active and passive transformation
이제 앞으로의 포스트에서 회전 행렬 이라 하면, 전부 벡터의 회전 변환의 관점에서 본 회전 행렬(Alibi)을 의미한다.