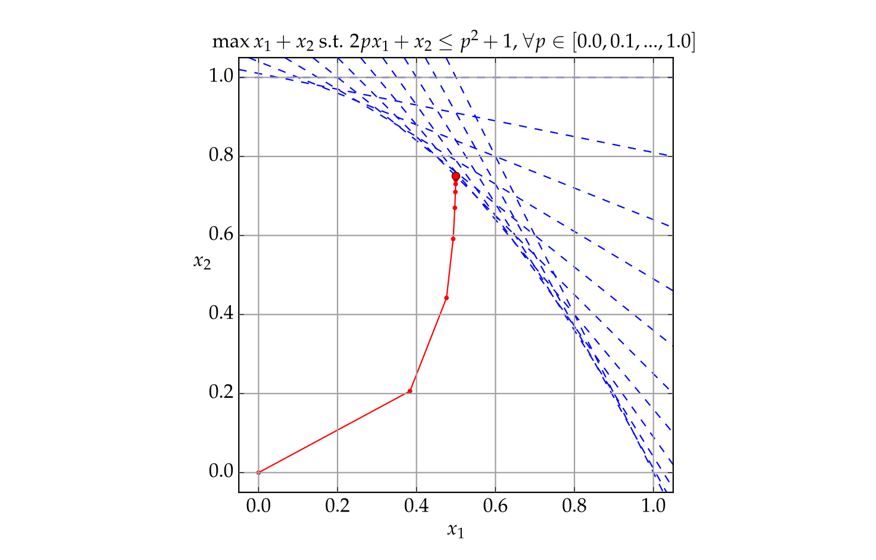
내부점 방법(Interior Point Method)
장벽을 높여가며 부등식 제약 조건 내부에서 최적해를 찾는 Interior Point Method에 대해 알아보자 참고 1 : Interior point method 참고 2 : 모두를 위한 컨벡스 최적화, barrior methods 참고 3 : CMU-convex optimiazation, barrior methods 참고 4 : Barr...

장벽을 높여가며 부등식 제약 조건 내부에서 최적해를 찾는 Interior Point Method에 대해 알아보자 참고 1 : Interior point method 참고 2 : 모두를 위한 컨벡스 최적화, barrior methods 참고 3 : CMU-convex optimiazation, barrior methods 참고 4 : Barr...

최적화 문제에서 최적 해를 찾는 필요,충분 조건 KKT 조건에 대해 알아보자 참고 1 : Karush-Kuhn-Tucker Conditions 참고 2 : 모두를 위한 컨벡스 최적화, KKT Conditions 참고 3 : CMU-convex optimiazation, KKT Conditions KKT condition은 어떠한 선형 또...

일반 문제(General Problem)의 쌍대성(Duality)과 Duality Gap에 대해 알아보자. 참고 1 : Duality (Optimization) 참고 2 : 모두를 위한 컨벡스 최적화, Duality in General Programs 참고 3 : CMU-convex optimiazation, Duality in Genera...
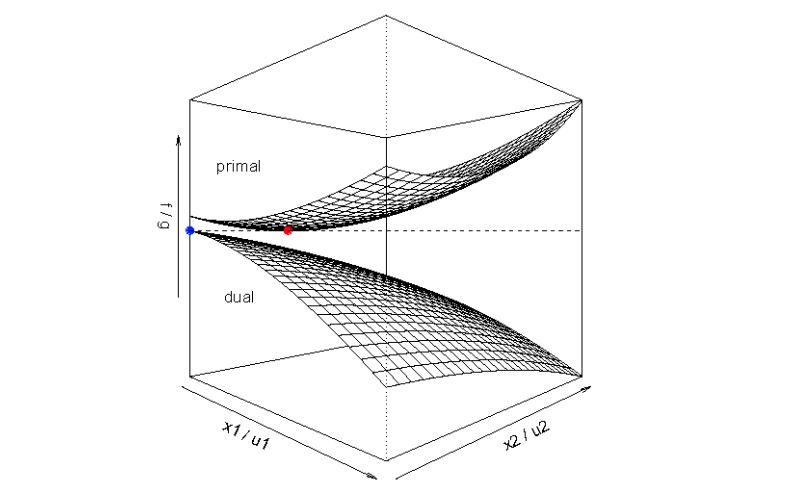
최적화 분야의 쌍대성(Duality)은 최적화 문제를 primal 문제와 dual 문제로 나누어서 생각하는 방법이다. 이번 포스트에서는 선형 프로그래밍(Linear Programming)에서의 duality에 대해 알아보도록 하자. 참고 1 : Duality (Optimization) 참고 2 : 모두를 위한 컨벡스 최적화, Duality ...

경사 하강법보다 일반적으로 더 빠른 수렴속도를 가진 Newton’s method 에 대해 알아본다. 참고 1 : Quasi-Newton method 참고 2 : 모두를 위한 컨벡스 최적화, Quasi-Newton method 참고 3 : CMU-convex optimiazation, Quasi-Newton method 기존 Newton ...

경사 하강법보다 일반적으로 더 빠른 수렴속도를 가진 Newton’s method 에 대해 알아본다. 참고 1 : Newton’s method in optimization 참고 2 : 모두를 위한 컨벡스 최적화, Newton’s method 참고 3 : CMU-convex optimiazation, Newton method Newton’s...
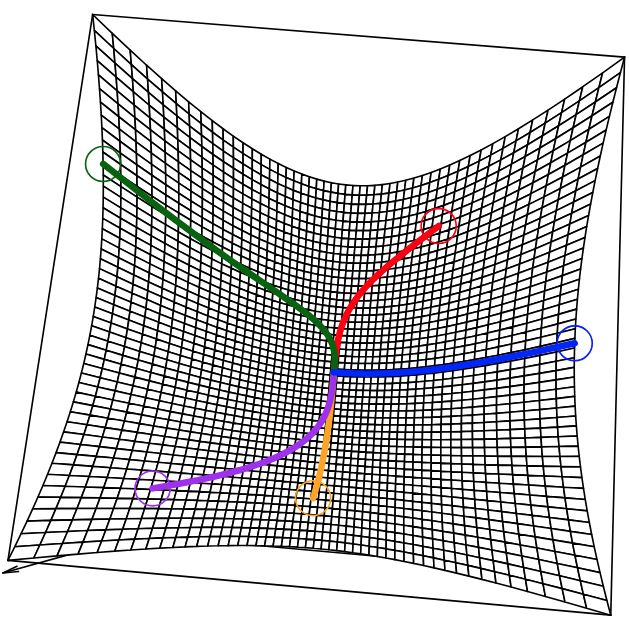
최적화 기법 중에 제일 기본적이고 중요한 경사 하강법에 대해 소개한다. 참고 1 : Gradient Descent 참고 2 : 모두를 위한 컨벡스 최적화, Gradient Descent 참고 3 : CMU-convex optimiazation, gradient descent 경사 하강법(Gradient descent) 기본 개념 경사 하...

제약이 있는 최적화 문제를 제약이 없는 최적화 문제로 바꾸는 라그랑주 승수(Lagrange multiplier)와 라그랑지안(Lagrangian)에 대해 알아보자 참고 1 : Lagrange multiplier 참고 2 : Bordered Hessian Matrix 참고 3 : 모두를 위한 컨벡스 최적화 - Convex Sets 참고 4...
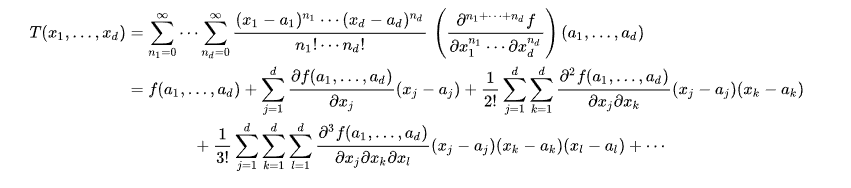
참고 : Taylor Series 다변수 함수의 테일러 확장은 어떻게 정의되고 왜 필요한지 살펴보자. 테일러 급수 역사 급수에 대한 고민은 고대 그리스 때부터 이어졌다. 제논의 역설(Zeno’s paradox)은 무한급수의 개념을 포함하고 있었으며, 이후에도 다양한 수학자들이 급수에 대한 연구를 이어왔다. 14세기의 인도 수학자 Madh...
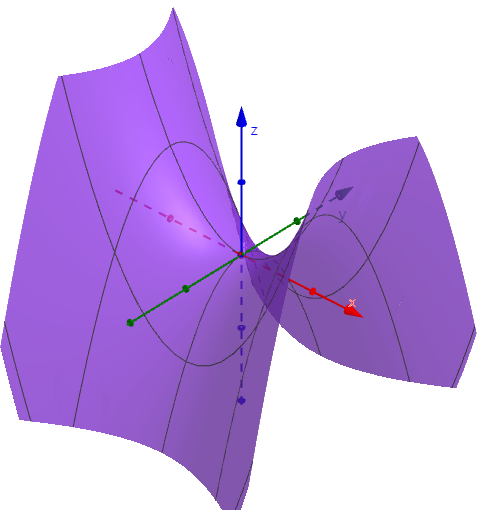
미분 가능한 다변수 함수의 극값과, 극대 극소 판별에 대해 다룬다. 참고 1 : 모두를 위한 컨벡스 최적화 참고 2 : Maximum & Minimum 참고 3 : Hessian Matrix 어떤 함수의 극점(extremum point), 그 중에서도 특히 극소점(local minimum point)은 최적화 문제에서 아주 중...