최적화란 무엇이고 왜 필요한가 참고 : 모두를 위한 컨벡스 최적화 이 카테고리의 거의 모든 내용은 모두를 위한 컨벡스 최적화 깃허브 페이지의 내용을 내가 공부하면서 정리한 것이다. 더 자세한 이론적인 내용은 위 링크를 참고하면 좋다. 최적화 문제의 정의 최적화는 어떤 함수의 값을 최소화 또는 최대화시키는 입력 변수들의 값을 찾는 ...

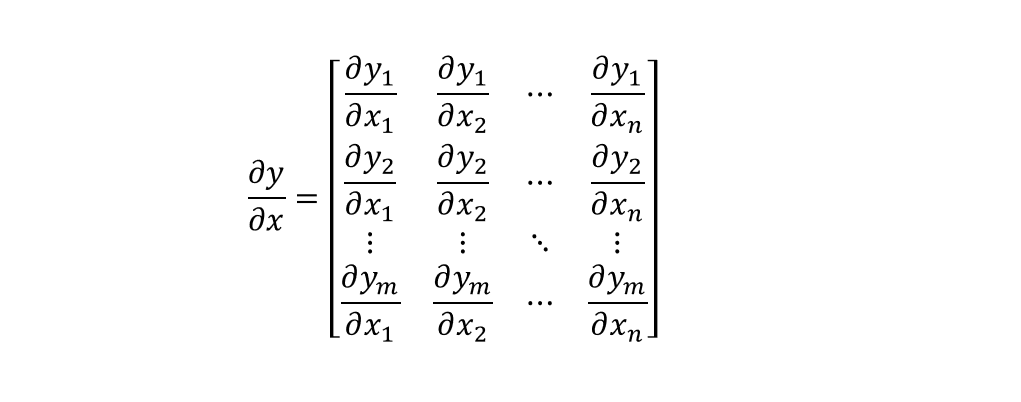
스칼라-벡터, 스칼라-행렬, 벡터-벡터 끼리의 편미분에 대하여. 참고 : Matrix calculus 행렬 미분이란 수학에서 행렬 미분이란 다변수 미적분학에서 사용하는 표기법이며, 특히 다변수의 편미분에 대한 표기를 다룬다. 기존의 변수가 하나 뿐이던 함수의 미분과 나름 유사한 편미분 법칙을 가지고 있다. 결과물이 행렬의 형태로 ...

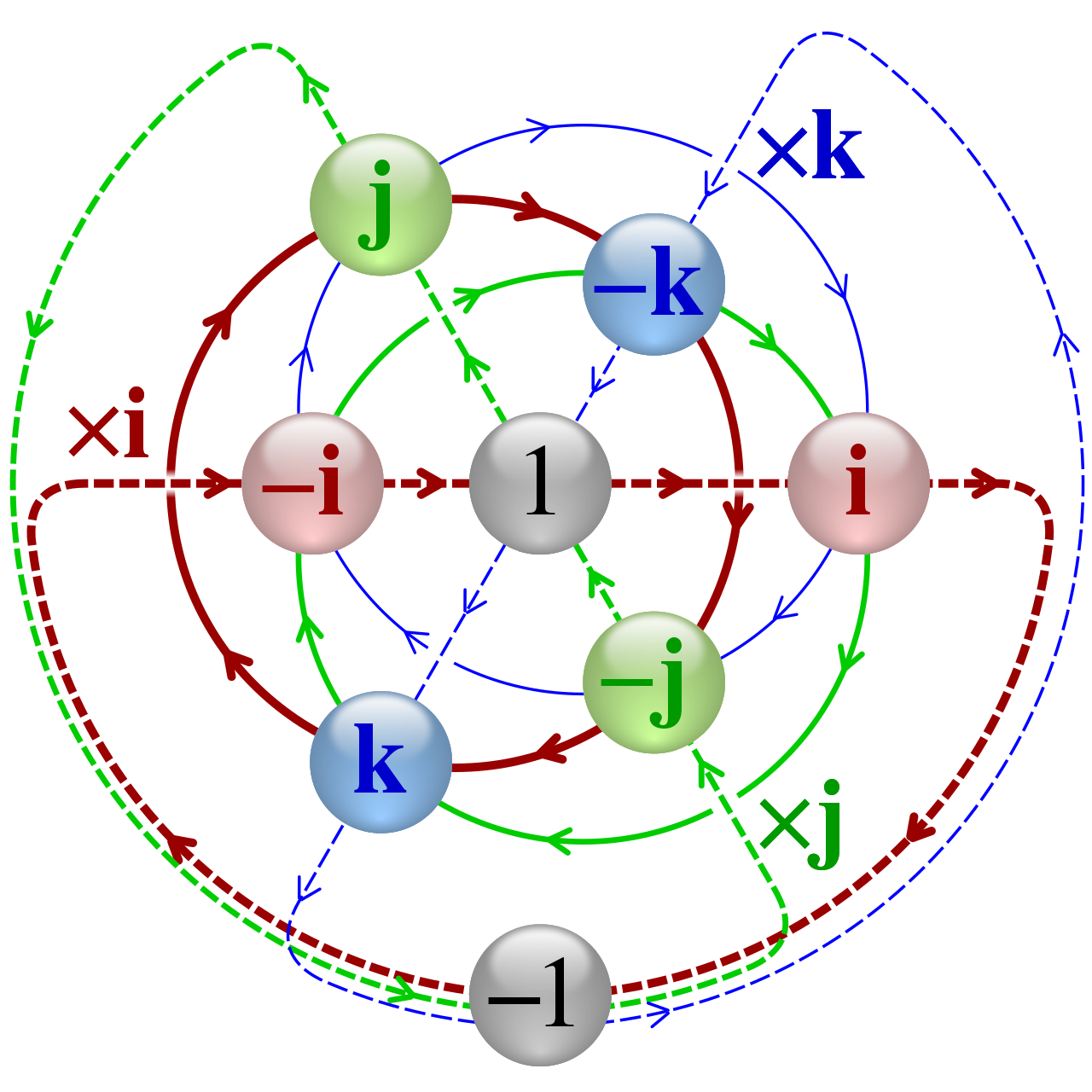
쿼터니언으로부터 회전 행렬을 유도해 본다. 쿼터니언의 미분과, 각속도 벡터와의 관계를 유도한다. 회전 행렬로의 변환 쿼터니언 $q = w + xi+yj+zk = w + \vec{v}$를 사용한 3차원 벡터의 회전 행렬을 유도해 본다. 앞서 쿼터니언의 곱에 대해 다음의 식이 성립함을 보고 가자 [\begin{align} &q_1,...

사원수를 사용해서 어떻게 3차원 벡터를 회전할 수 있을까? 직전 포스트에서 다룬 쿼터니언 곱의 행렬 형태로부터 출발해 보자. 쿼터니안 곱의 행렬과 벡터 표현 임의의 두 쿼터니언 $q_1, q_2$에 있어서, 쿼터니언 곱의 행렬 표현은 다음과 같다. [\begin{align} q_1 \otimes q_2 &= [q_1]\times ...

사원수(쿼터니언, Quaternion)은 대체 무엇일까 참고 및 출처: Quaternion 3차원 회전의 완전체, 사원수에 대한 기본 개념들을 알아보자. 쿼터니언의 정의 사원수(Quaternion)은 3차원에서 벡터의 회전, 또는 물체의 자세를 표현하는 수학적인 방법 중 하나이다. 쉽게 생각해서 2차원의 자세를 표현하는 수가 복소수였다면,...

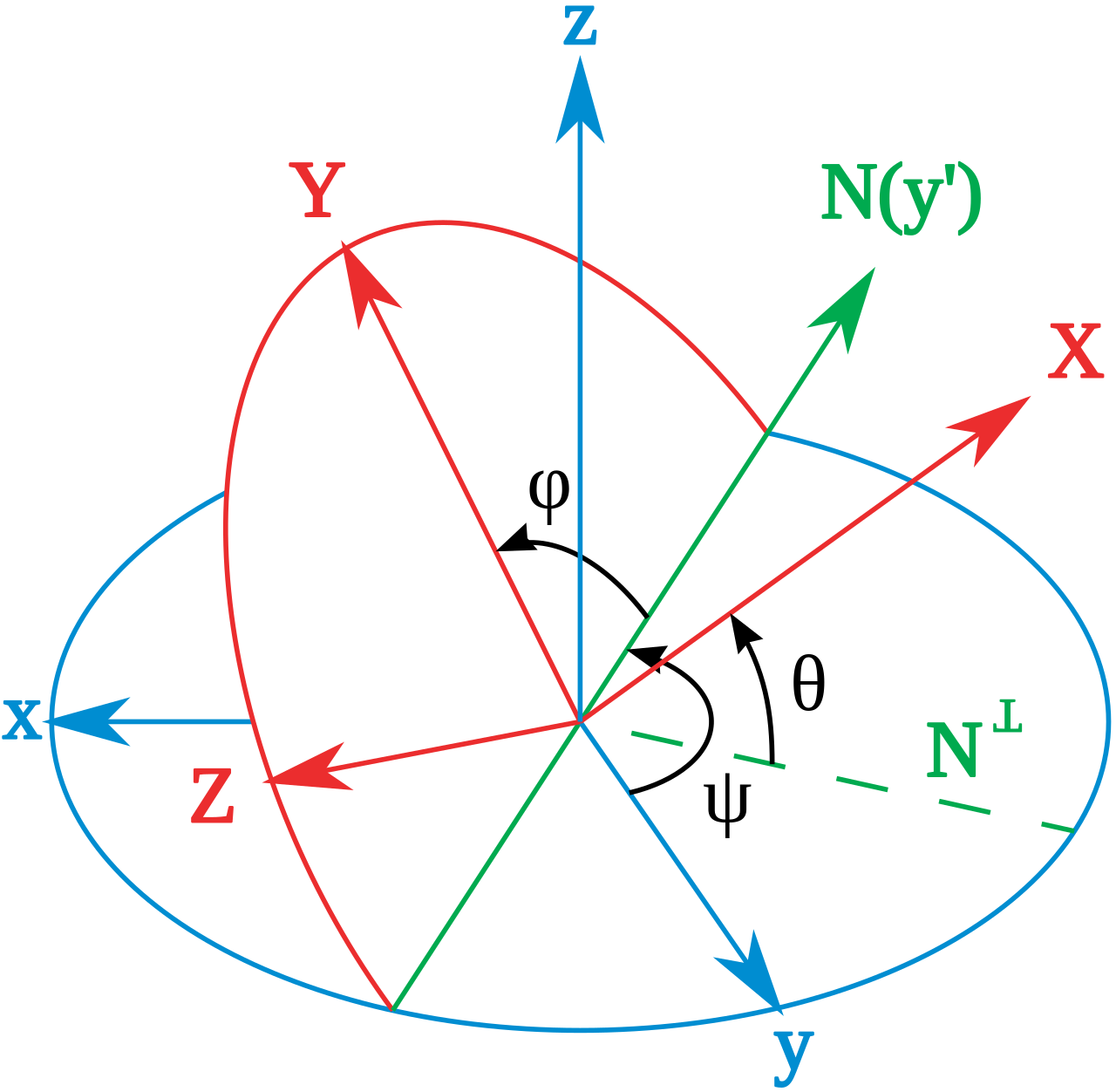
오일러가 제안했던 3차원 회전 방식, 오일러 각(Euler Angle)에 대해 알아보자 참고 : Euler Angles 오일러각은 그림 그리기도 너무 까다롭고, 내용도 중구난방이 많아서, 영문 위키를 많이 참조했다. 오일러와 3차원 회전 오일러는 1775년 오일러 각(Euler Angle)과 오일러의 회전 정리(Euler’s Rot...

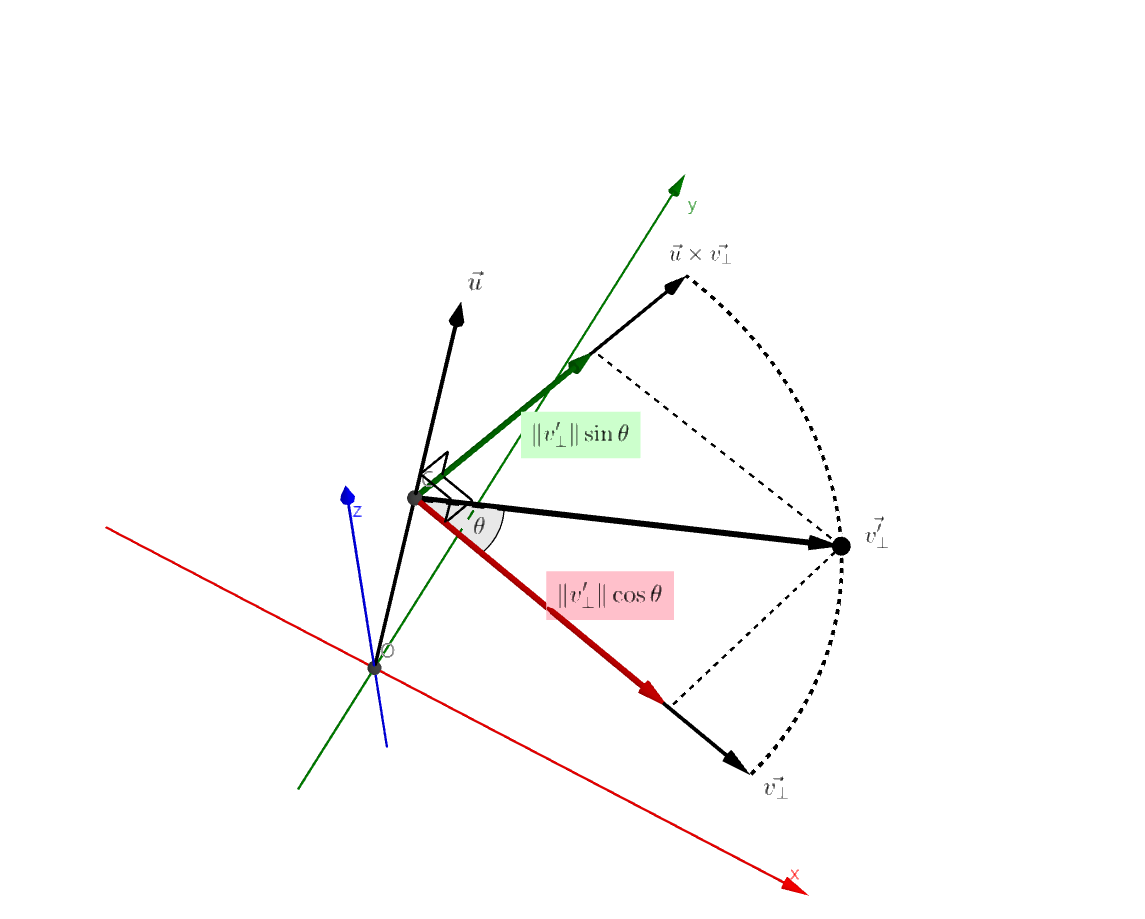
임의의 축에 대한 벡터의 회전, 로드리게스 회전에 대해 알아보자. 참고 : Rodrigues’ rotation formula 로드리게스 회전 공식 지금까지 2D 평면에서는 회전축이 항상 평면에 수직인 축 (가상의 $z$축)이었기에, 회전된 각도 $\theta$만으로 결정할 수 있었다. 하지만 3D 공간에서는 회전축이 완전한 자유도를...

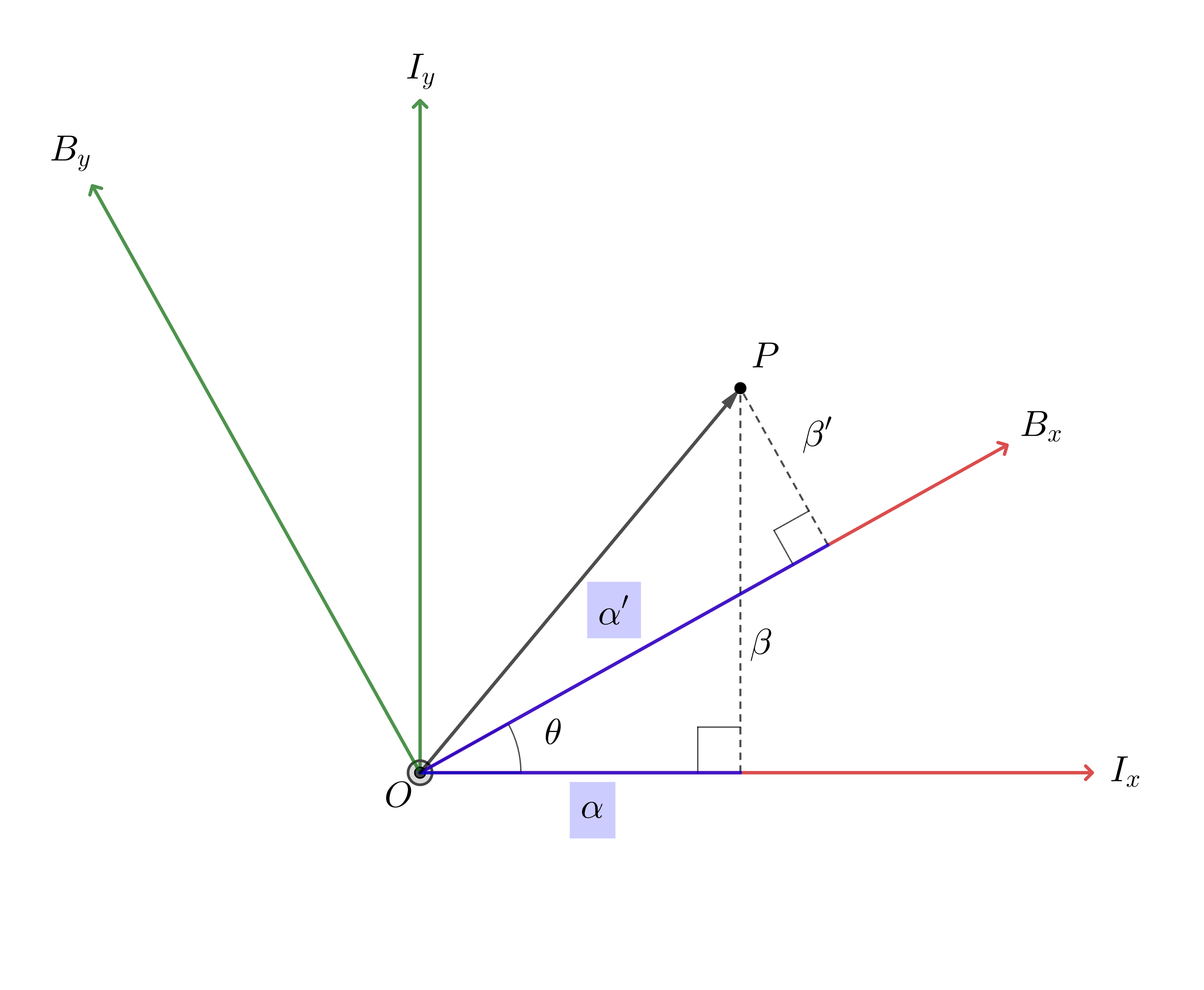
회전변환의 변환은 또 뭔 회전 변환 행렬 자체의 프레임 회전 변환에 대해 알아보자 벡터의 회전과 프레임의 회전 변환에 대해서는 이 포스트를 참고하자. 프레임 회전 변환 이전 포스트에서, 회전변환행렬 $R$을 사용해서 점 P가 어떻게 회전되는지 보였다. 그림 1: 고정된 점 P를 표현하는 2개의 프레임 좌표 그림1을 보자. 공간상에 ...

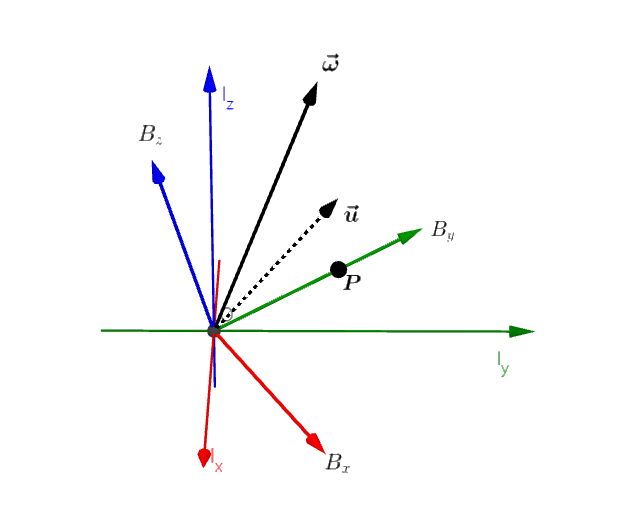
3차원 회전 행렬을 미분하여 각속도 벡터를 유도해 보자 앞서서 2차원 회전 행렬과 각속도의 관계를 행렬의 미분을 통해 알아보았다. 그렇다면 3차원 역시도 회전 행렬을 미분하여 각속도 벡터를 유도할 수 있는가? 된다면 그 관계는 어떻게 될 것인가. 행렬곱의 미분 유도에 앞서, 먼저 짚고 넘어가야할 점은 행렬곱의 미분이다. 말은 어렵게 했...

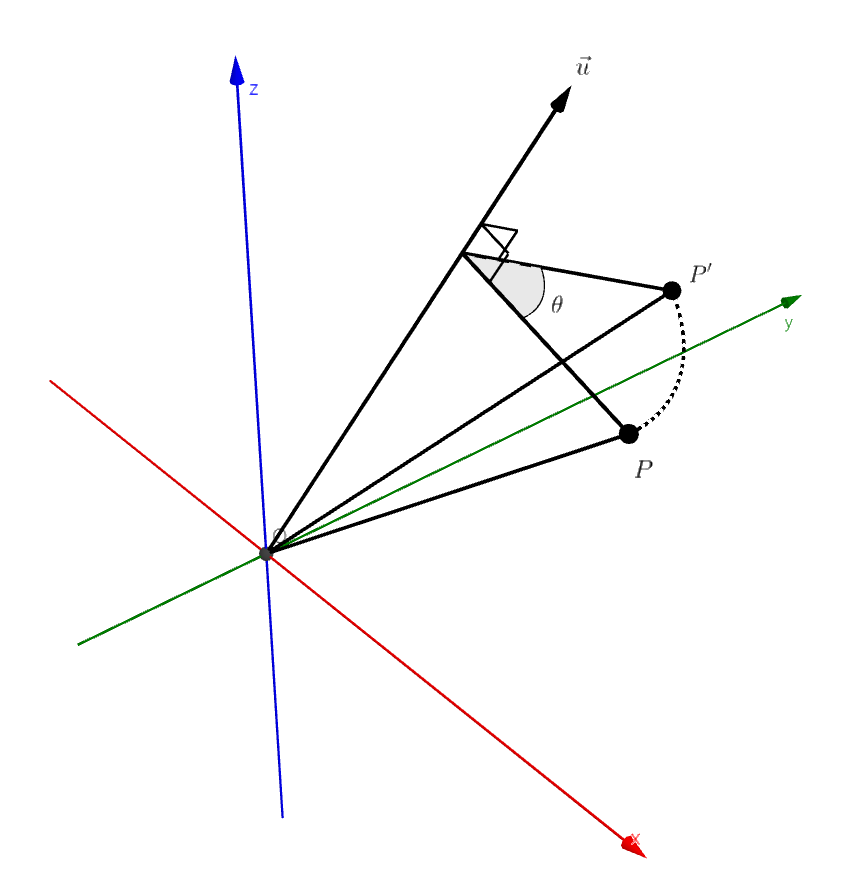
2차원의 회전과 3차원의 회전은 무엇이 다른가 차원의 차이 너무나 당연한 사실이겠지만, 2차원 회전은 평면상에서 원점을 중심으로 회전한다. 하지만 3차원 회전은 공간상에서 원점을 지나는 임의의 축을 중심으로 회전한다. 그림 1 : 임의의 축 u를 중심으로 회전하는 점 P 회전 행렬의 차이 2차원 회전 행렬은 2개의 축 벡터를 변환했기...