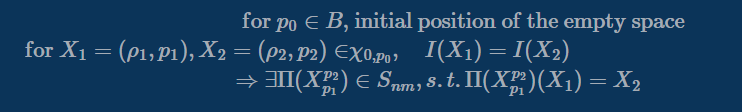
슬라이딩 퍼즐의 도달 가능성(문제 정의)
슬라이딩 퍼즐의 도달 가능성에 대해 알아보기 전에, 이 포스트에서 다룰 문제를 명확히 정의하고자 한다. 앞서서 슬라이딩 퍼즐의 불변량에, 군과 대칭군의 여러 성질들을 알아보았지만, 아직까지도 슬라이딩 퍼즐의 도달 가능성에 대해서는 명확히 정의하지 않았다. 왜냐하면 퍼즐 자체에 대한 여러가지 정의가 모호했기 때문이다. 예를 들어서 퍼즐을 푸...
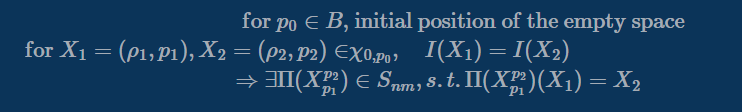
슬라이딩 퍼즐의 도달 가능성에 대해 알아보기 전에, 이 포스트에서 다룰 문제를 명확히 정의하고자 한다. 앞서서 슬라이딩 퍼즐의 불변량에, 군과 대칭군의 여러 성질들을 알아보았지만, 아직까지도 슬라이딩 퍼즐의 도달 가능성에 대해서는 명확히 정의하지 않았다. 왜냐하면 퍼즐 자체에 대한 여러가지 정의가 모호했기 때문이다. 예를 들어서 퍼즐을 푸...
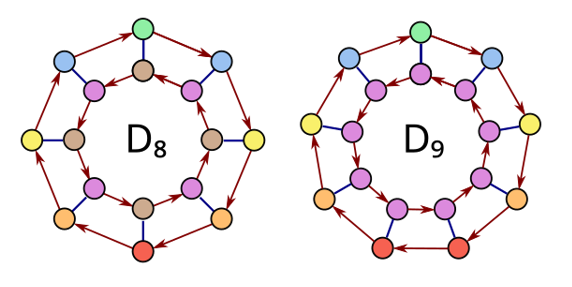
모든 순열을 만들어 내는 법 참고 1 : https://en.wikipedia.org/wiki/Parity_of_a_permutation 참고 2 : https://dec41.user.srcf.net/notes/IA_M/groups.pdf 참고 3 : https://jweilhammer.github.io/sliding-puzzle-sol...
슬라이딩 퍼즐이 항상 유지하는 어떠한 성질은 무엇인가 참고 1 : https://en.wikipedia.org/wiki/Parity_of_a_permutation 참고 2 : https://dec41.user.srcf.net/notes/IA_M/groups.pdf 참고 3 : https://en.wikipedia.org/wiki/15_p...
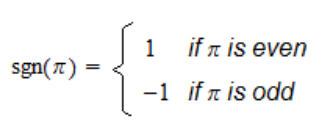
순열의 부호란 무엇이며, 어떤 성질이 있을까? 참고 1 : https://en.wikipedia.org/wiki/Parity_of_a_permutation 참고 2 : https://en.wikipedia.org/wiki/Alternating_group 참고 3 : https://dec41.user.srcf.net/notes/IA_M/g...
군 동형과 케일리 정리란 무엇일까? 왜 ‘대칭군’ 이라는 거창한 이름이 붙을 수 있었을까? 참고 1 : https://en.wikipedia.org/wiki/Cayley%27s_theorem 참고 2 : https://dec41.user.srcf.net/notes/IA_M/groups.pdf 케일리 정리(Cayley’s theorem...
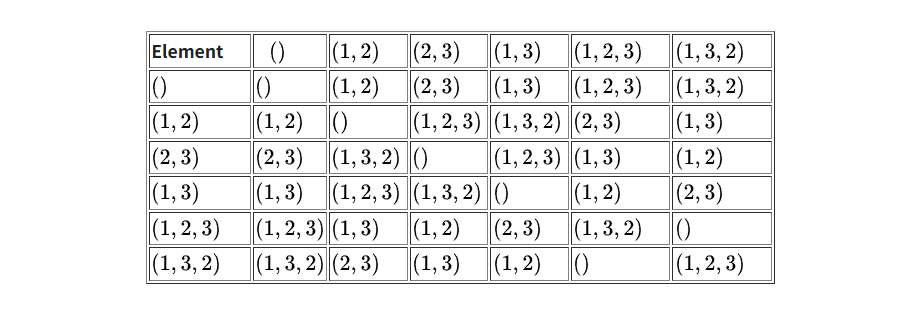
대칭군이란 무엇이고, 왜 이렇게 중요하게 다뤄질까? 참고 1 : https://en.wikipedia.org/wiki/Symmetric_group 참고 2 : https://dec41.user.srcf.net/notes/IA_M/groups.pdf 대칭군이란 대칭군(Symmetric group)란, 주어진 집합의 모든 순열(perm...
부분군이란 무엇이고 어떠한 기본 성질들이 있을까? 참고 1 : https://en.wikipedia.org/wiki/Subgroup 참고 2 : https://dec41.user.srcf.net/notes/IA_M/groups.pdf 부분군이란 부분군(Subgroup)이란, 군 $G$의 부분집합인데, 그 역시도 군의 성질을 만족하는...
군이란 무엇이고 어떤 기본 성질이 있을까? 참고 1 : https://en.wikipedia.org/wiki/Group_(mathematics)# 참고 2 : https://dec41.user.srcf.net/notes/IA_M/groups.pdf 서론 슬라이딩 퍼즐의 해결 가능성 문제를 군론을 통해 접근하려면, 군론의 기초 개념들...
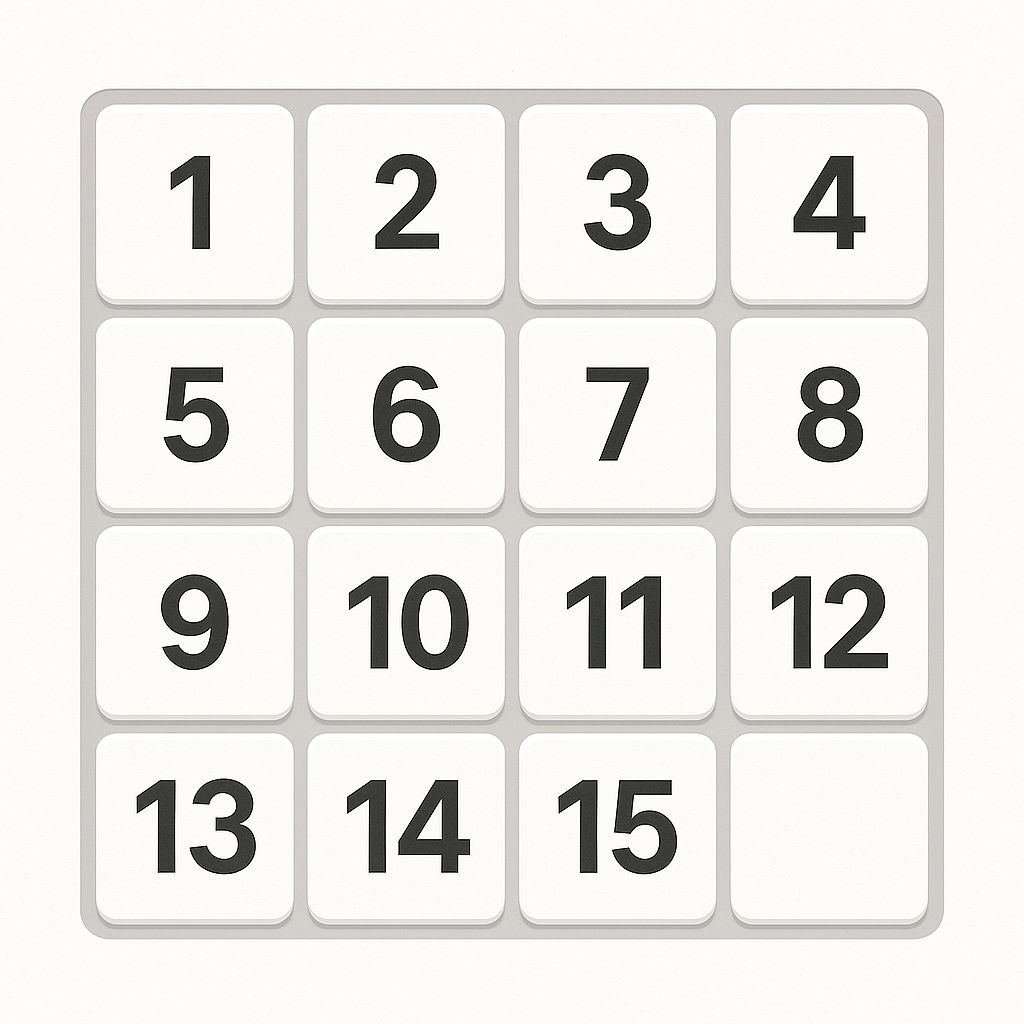
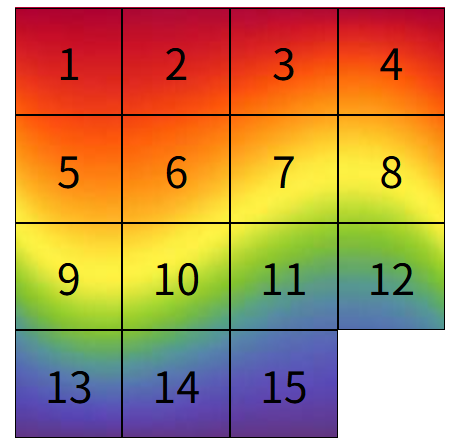
슬라이딩 퍼즐 조각을 흩었다가 아무렇게나 다시 조립했을 때, 그 슬라이딩 퍼즐을 풀 수 있을 확률이 어떻게 될까? 서론 슬라이딩 퍼즐을 모르는 사람은 없다. 원래의 이미지를 각 칸으로 나누고, 빈칸을 하나 남겨서 그 빈칸을 이리저리 슬라이드 시켜가며 맞추는 간단한 퍼즐. 이 퍼즐을 맞추는 방법은 널리 알려져 있고, 각각의 조각의 원래 위치...
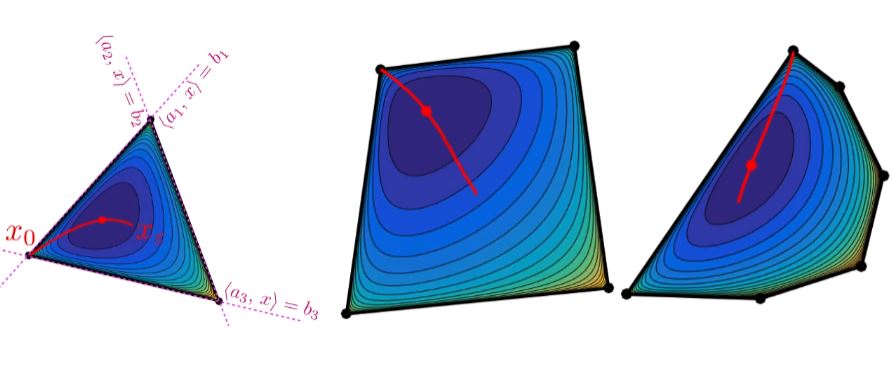
primal 과 dual 문제를 동시에 고려하여 centering step을 한단계로 줄이는 primal-dual interior point method에 대해서 알아보자. 참고 1 : Interior point method 참고 2 : 모두를 위한 컨벡스 최적화, primal-dual interior point method 참고 3 : C...